Системы линейных уравнений

Матрицы

Числовой матрицей размера 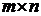называют таблицу из строк и столбцов, состоящую из чисел и имеющую вид

.

В случае матрица называется квадратной.

Частным случаем матрицы можно считать -мерный вектор, заданный своими координатами. Его можно рассматривать либо как матрицу-строку размером , либо как матрицу-столбец размером .

Матрицы имеют приложения в экономике при построении математической модели межотраслевого баланса производства и распределения продукции. В частности, в этой модели строится квадратная таблица учета продукции, производимой и потребляемой различными отраслями. Для этого составляют квадратную таблицу, размер которой определяется количеством отраслей (n):

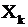. Каждая отрасль () не только производит какую-то продукцию, но и потребляет продукцию. Например, легкая промышленность потребляет энергию (энергетика), станки (машиностроение), а также частично потребляет свою же собственную продукцию –изделия легкой промышленности. Машиностроение потребляет энергию (энергетика), продукцию легкой промышленности и частично свою собственную продукцию, так как, например, швейные машинки, необходимые легкой промышленности, изготавливаются машиностроением с помощью станков, произведенных машиностроением для машиностроения. …

Квадратная матрица учета продукции состоит из элементов , представляющих стоимость части продукции, произведенной в i- й отрасли для нужд j- й отрасли.

Действия над матрицами.

1. Для матриц можно определить умножение на число. Для этого на данное число умножаются все элементы матрицы.

.

2. Для матриц одного размера определяется операция сложения: новая матрица имеет элементами суммы соответствующих элементов исходных матриц.

.

3. Для того чтобы умножить одну матрицу на другую, необходимо соответствие размеров матриц: количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы. Пусть матрица размера 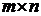с элементами умножена на матрицу размера с элементами Результатом умножения является матрица размера , элементы которой получаются следующим образом:

Заметим, что умножение матриц некоммутативно, то есть, в общем случае даже когда и – квадратные матрицы одного размера.

mult.wxm

4. Транспонирование матрицы. Если 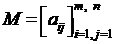, то транспонированной к этой матрице является матрица . Таким образом, для транспонирования следует сделать строки столбцами, а столбцы строками. В случае, когда матрица квадратная, получение транспонированной матрицы означает симметричное отражение элементов исходной матрицы относительно диагонали, соединяющей левый верхний и правый нижний элементы матрицы (главной диагонали).

Определители

Каждой квадратной матрице можно поставить в соответствие число, называемое определителем матрицы и обозначаемое

.

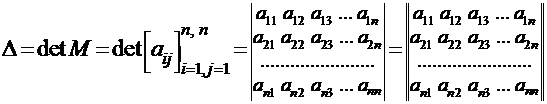В определителе различают главную диагональ (слева направо, сверху вниз) и побочную диагональ (слева направо, снизу вверх).

Определитель вычисляется методом разложения по ряду (строке или столбцу) путем сведения определителя -го порядка к линейной комбинации определителей -го порядка. Каждый новый определитель также сводится к вычислению определителей меньшего – уже -го – порядка…. И так последовательно вычисление определителя любого порядка сведется к вычислению определителей 2-го порядка.

Вычисление определителя 2-го порядка: 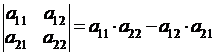, то есть от произведения чисел на главной диагонали вычитается произведение чисел на побочной диагонали.

Для вычисления определителя высокого порядка следует ввести понятие минора. Минором , соответствующим элементу называют определитель, полученный из исходного определителя вычеркиванием 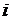-й строки и -го столбца.

Теперь в соответствии с правилом вычисления определителя

,

где первое выражение – разложение заданного определителя по 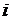-й строке, а второе – по -му столбцу. Способ выбора строки или столбца произволен, однако при устном вычислении проще выбирать тот ряд, где большее число нулевых элементов.

В частности, вычисление определителя 3-го порядка сводится к сумме шести произведений по три элемента, лежащих на разных строках и столбцах. Произведения берутся со знаком +, если эти три элемента лежат на главной диагонали или являются вершинами треугольника с основанием, параллельным главной диагонали. Произведения берутся со знаком -, если три элемента лежат на побочной диагонали или являются вершинами треугольника с основанием, параллельным побочной диагонали:

,

Можно вычислять определитель третьего порядка также следующим способом: присоединим к исходной матрице снизу две ее первых строки и пройдем по направлениям главной диагонали, перемножая стоящие на соответствующих прямых три элемента и складывая со знаком +, затем пройдем по направлениям побочной диагонали, перемножая стоящие на соответствующих прямых три элемента и складывая со знаком –.

Правила вычисления основаны на следующих свойствах определителей.

1. При перестановке двух строк или двух столбцов знак определителя меняется на противоположный:

.

2. Из строки или столбца можно выносить общий множитель за знак определителя: .

3. Если каждый элемент строки (столбца) представим в виде суммы, то такой определитель равен сумме двух определителей, у которых в этой строке (столбце) стоят соответствующие слагаемые:

.

Из представленных свойств следуют новые свойства:

4. Определитель с двумя строками (столбцами), отличающимися коэффициентом, равен нулю.

5. Определитель, у которого есть строка (столбец), представляющая линейную комбинацию других строк (столбцов), равен нулю.

6. Если заменить в определителе строки на столбцы, а столбцы на строки – этот процесс называется транспонированием и представляет зеркальное отражение определителя относительно главной диагонали – определитель не изменится.

Современные компьютерные средства позволяют мгновенно вычислять различные действия с матрицей. Например, пакет программ MAXIMA дает возможность вводить матрицу, а затем вычислять ее определитель.

matr.wxm

 

Системы линейных уравнений

В данном разделе нас будут интересовать возможность решения систем линейных уравнений, то есть, систем вида

где – известные числа, а – неизвестные, которые нужно найти, решив систему, .

Система линейных уравнений с использованием правила умножения матриц может быть записана в виде: , где , , .

 

Если число переменных системы больше числа уравнений , система оказывается недоопределенной, и если имеет решения, то их бесконечное множество. В случае, когда , система оказывается переопределенной и может не иметь решений. При любом соотношении между числом неизвестных и уравнений системы для решения или исследования системы линейных уравнений можно применять следующий метод.

Метод Гаусса

О снован данный метод на том, что при замене одного выбранного уравнения системы новым уравнением, полученным прибавлением к обеим частям данного уравнения соответствующих частей другого уравнения, умноженным на одно и то же число, получившееся система будет эквивалентна данной, то есть обе системы будут иметь одно и то же то же решение или одновременно будут неразрешимыми.

Суть метода в том, что последовательно исключаются неизвестные из уравнений системы. Рассмотрим исходную систему. Предположим, что мы хотим исключить переменное 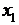из всех уравнений, кроме одного – первого из уравнений системы. В таком случае в качестве первого уравнения в системе мы должны выбрать то, где коэффициент при 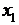отличен от нуля. Предположим, что . Изменим второе уравнение системы, прибавив к обеим его частям обе части первого уравнения, умноженные на число . В новом втором уравнении уже не будет члена с 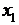. Теперь изменим третье уравнение системы, прибавив к обеим его частям обе части первого уравнения, умноженные на число . В новом третьем уравнении также не будет члена с 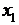…. Проделав эту операцию со всеми уравнениями системы, мы получим новую систему, эквивалентную данной и содержащую 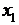только в первом уравнении. Теперь исключим неизвестное из всех уравнений, кроме первого и второго. Для этого на второе место поставим то уравнение системы, не содержащее 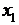, в котором коэффициент при не равен нулю. Будем прибавлять обе части этого уравнения, умноженные на соответствующее число, к соответствующим частям всех уравнений, начиная с третьего, чтобы уничтожить в них члены с ….. Проделав это со всеми уравнениями системы и последовательно со всеми неизвестными, мы можем получить следующие варианты эквивалентных систем.

А) В случае, когда , мы либо придем к системе, где последнее уравнение содержит неизвестное, либо получим на каком-то этапе невозможное соотношение, когда ноль равен числу, отличному от нуля. В первом случае система имеет бесконечное множество решений, так как первые неизвестных выражаются линейно через оставшиеся неизвестные. Во втором случае система несовместна, то есть, не имеет решений.

Б) В случае, когда , мы можем прийти к системе, в котором 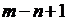последних уравнений одинаковы и представляют собой одно и то же выражение для . В этом случае система имеет единственное решение. Если же на каком-то этапе получится соотношение, где ноль равен числу, отличному от нуля, то система несовместна.

В) В случае, когда , мы также можем на каком-то этапе получить соотношение, где ноль равен числу, отличному от нуля. Такая система несовместна. В противном случае в последнем уравнении определяется неизвестное , а из предыдущих уравнений определяются последовательно и однозначно все другие неизвестные. В этом случае система имеет единственное решение.

П р и м е р. Решим методом Гаусса систему Сначала с помощью первого уравнения исключим x из второго и третьего уравнений: к обеим частям второго уравнения прибавим части первого уравнения, умноженные на -3, а к обеим частям третьего уравнения прибавим соответствующие части первого уравнения. Получим эквивалентную систему

Теперь исключим y из последнего уравнения, умножив обе части второго уравнения на -4 и прибавив к обеим частям третьего уравнения. Получим систему с треугольной левой частью: Теперь из последнего уравнения мы имеем: . Зная это значение, получим y из второго уравнения: . И наконец, значение определим из первого уравнения.

Для систем, где число уравнений и неизвестных совпадают, возможно применение следующего метода, основанного на вычислении определителей.

Метод Крамера

Определители играют большую роль в решениях линейных систем из уравнений относительно неизвестных

Существует правило Крамера решения системы (4), в соответствии с которым где – главный определитель системы, а – также определитель -го порядка, отличающийся от 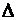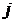-м столбцом: он заменен столбцом из свободных членов .

Очевидно, что правило Крамера применимо, если , и при исходная система имеет единственное решение. В том случае, если и существует хотя бы один из определителей такой, что , система не имеет решений.

Если и , это означает, что хотя бы одно из уравнений исходной системы является линейной комбинацией других уравнений, и его можно удалить из системы. Остается система из уравнения относительно неизвестных. В ее левой части ищем среди определителей определитель -го порядка отличный от нуля. Берем систему с этим главным определителем, а столбец слагаемых, содержащих переменное , коэффициенты при котором не вошли в этот определитель, переносим в правую часть. Решая новую систему по правилу Крамера, получим решение, зависящее от . Если среди определителей -го порядка нет ненулевых, убираем еще одно уравнение из системы и снова ищем хотя бы один ненулевой определитель, уже -го порядка….

 

П р и м е р. Решим систему из предыдущего примера методом Крамера. Сначала сосчитаем главный определитель системы: . Затем найдем все определители, где столбцы главного определителя заменяются последовательно столбцами свободных членов: .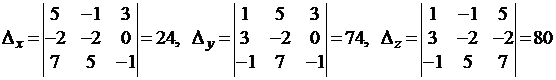

В соответствии с формулами Крамера .

Современные пакеты математических программ позволяют решать системы, не прибегая к вычислению определителей. Однако необходимо понимать, почему система, решаемая с помощью компьютера, может не иметь решений или иметь много решений.

Решение систем линейных уравнений в пакете программ MAXIMA проводится следующим образом:

Syst.wxm