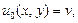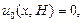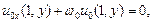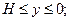УДК 517.9
ЗАДАЧА ПРИБЛИЖЕННОГО АНАЛИЗА СВОБОДНОЙ ГРАНИЦЫВ УПРАВЛЕНИИ ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫМИ ТЕХНОЛОГИЯМИ
Миненко А.С., Радевич Е.В., Лёвкина А.В.
ГОУ ВПО «Донецкий национальный технический университет»
ДНР, г. Донецк
Аннотация. В данной статье исследуется задача о моделировании процесса кристаллизации металла. Проводится приближенный анализ свободной границы, который зависит от интенсивности вихря. Основное внимание уделяется разработке методов решения нелинейных краевых задач и задач на экстремум функционалов.
Ключевые слова: задача, моделирование, металл, информационно-коммуникационные технологии, управление, свободная граница, вихрь.
THE PROBLEM OF THE FREE BOUNDARY OF APPROXIMATE ANALYSIS IN THE MANAGEMENT OF INFORMATION AND COMMUNICATION TECHNOLOGIES
Minenko A. S., Lovkina A.V., Radevich E.V.
Donetsk National Technical University, DNR, Donetsk
Abstract. This article investigates the problem of modeling the process of crystallization of metal. An approximate analysis of the free boundary, which depends on the intensity of the vortex, is carried out.
Key words: problem, modeling, metal, information and communication technologies, control, free boundary, vortex.
Спецметаллургия является отраслью промышленности влияющей на экономику региона. В описанной выше отрасли рассмотрим процесс кристаллизации металла. Данный процесс весьма затруднительно реализовать практически, поэтому приводится математическая модель.
Начнем построение математической моделей с описания основных параметров, удовлетворяющих определенным законам. Рассмотрев задачу, приходим к выводу, что использование нелинейных моделей дает возможность описывать реальные процессы. В современном мире проблема построения нелинейных моделей, все еще актуальна в экономике и других отраслях при решении задач управления.
Постановка задачи.
Пусть  - это стационарный случай, обозначающий полосу. Тогда, кривую, отделяющую жидкую фазу
- это стационарный случай, обозначающий полосу. Тогда, кривую, отделяющую жидкую фазу  от твердой фазы
от твердой фазы  , обозначим через
, обозначим через 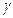 . Предположим, что температурное поле - монотонно убывает вместе с вертикальной координатой
. Предположим, что температурное поле - монотонно убывает вместе с вертикальной координатой  . Следовательно, твердая фаза расположена в нижней части полосы, а жидкая – в верхней. А односвязными и симметричными относительно оси
. Следовательно, твердая фаза расположена в нижней части полосы, а жидкая – в верхней. А односвязными и симметричными относительно оси  - предполагаются области
- предполагаются области  и
и  . Пусть
. Пусть  - функция тока удовлетворяющая уравнению:
- функция тока удовлетворяющая уравнению:


 (1)
(1)
где  будет заданным достаточно малым численным параметром. Граничным условием для функции
будет заданным достаточно малым численным параметром. Граничным условием для функции  является следующее утверждение:
является следующее утверждение:

 (2)
(2)
Функция тока тождественно исчезает при  а следовательно, можно сделать вывод, что конвекции в жидкой фазе нет. Тогда, температуру в жидкой фазе обозначим через
а следовательно, можно сделать вывод, что конвекции в жидкой фазе нет. Тогда, температуру в жидкой фазе обозначим через  и уравнение конвективного теплопереноса будет иметь такой вид:
и уравнение конвективного теплопереноса будет иметь такой вид:


 (3)
(3)
Обозначим граничные условия для жидкой фазы:

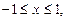
 (4)
(4)

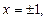
 (5)
(5)

 (6)
(6)
Обозначим температуру твердой фазы через  , которая удовлетворяет следующему уравнению
, которая удовлетворяет следующему уравнению

 (7)
(7)
Зададим условие третьего рода на вертикальной части границы твердой фазы:

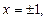
 (8)
(8)
 при
при  (9)
(9)

 (10)
(10)
Если  подлежит определению, то необходимо дополнительно задать закон сохранения энергии, тогда получим:
подлежит определению, то необходимо дополнительно задать закон сохранения энергии, тогда получим:



 (11)
(11)
Задача (1) – (11) является задачей нелинейной и «основное» неизвестное – это граница  , а метод решения таких задач [1], состоит в разложении в ряд по степеням малого параметра
, а метод решения таких задач [1], состоит в разложении в ряд по степеням малого параметра  .
.
Линеаризация задачи по интенсивности вихря
Будем считать, что неизвестные рассматриваемой задачи можно представить в виде степенного ряда по 
 (12)
(12)
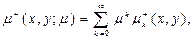 (13)
(13)
 (14)
(14)
Если свободная граница  имеет явное представление, тогда
имеет явное представление, тогда

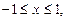 (15)
(15)

 (16)
(16)
Подставив эти разложения в задачу (1) – (11) и приравняв их члены друг другу, при одинаковых степенях  , получим бесконечное число задач. Выпишем нулевое приближение, которое соответствует
, получим бесконечное число задач. Выпишем нулевое приближение, которое соответствует  в нулевой степени. Из уравнения (1) получим функцию
в нулевой степени. Из уравнения (1) получим функцию  , которая является гармоничной и удовлетворяет нулевым граничным условиям Дирихле, тогда
, которая является гармоничной и удовлетворяет нулевым граничным условиям Дирихле, тогда  в
в  .
.
Тогда условия, определяющие  имеют следующий вид:
имеют следующий вид:

 (17)
(17)

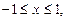 (18)
(18)

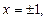
 (19)
(19)

 (20)
(20)

 (21)
(21)
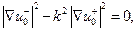
 (22)
(22)
Задачи (17) – (22) имеют единственное классическое решение [1, 2] в классе функций 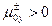 и
и  в
в  и
и 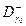 . Монотонно возрастающая, в правой половине, граница
. Монотонно возрастающая, в правой половине, граница  , называется аналитической кривой. Тогда, за исключением угловых, точек функции
, называется аналитической кривой. Тогда, за исключением угловых, точек функции 
 непрерывны в
непрерывны в  и
и  соответственно и непрерывно дифференцируемы всюду.
соответственно и непрерывно дифференцируемы всюду.
Тогда частным случаем решаемой задачи, является утверждение:
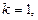
 (23)
(23)
Если ввести замену, тогда первое условие всегда выполнимо:

| 
|
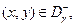
|
И приведет задачу (17) – (22) к случаю  . Исходя из вышеизложенного на
. Исходя из вышеизложенного на  будут выполнятся следующие условия:
будут выполнятся следующие условия: 
 . А значит (17) – (22) является обычной задачей о распределении температуры в области
. А значит (17) – (22) является обычной задачей о распределении температуры в области  не включая фазовые превращения вещества, таким образом строим функцию
не включая фазовые превращения вещества, таким образом строим функцию  по формуле
по формуле

| 
| (24) |

|
тогда решение задачи имеет следующий вид:
| (25) |
Из всего изложенного сделаем вывод, что функция 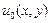 может быть эффективно найдена при помощи метода Фурье. А относительно функции
может быть эффективно найдена при помощи метода Фурье. А относительно функции 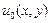 можно сделать вывод, что
можно сделать вывод, что 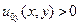 в области
в области  [3]. Тогда, уравнение
[3]. Тогда, уравнение 
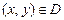 всегда разрешимо в виде некоторой функции
всегда разрешимо в виде некоторой функции  которая задает кривую
которая задает кривую  , т.е.
, т.е.