Эвристический метод кодирования рассмотрим на данном примере.
Для автомата Мура построим матрицу М, состоящую из номеров состояний, для которых есть переходы в таблице переходов. Причём она строится таким образом, чтобы один из элементов данной строки содержался в предыдущей.
Закодируем состояния из первой строки матрицы
a0=000, a1=001.
На карте Карно отметим закодированные состояния:
Таблица 4.11 – Закодированные состояния на карте Карно.
| Q1\Q2Q3 | ||||
Из матрицы М вычеркнем строки, состоящие из закодированных состояний. Получим матрицу М’.
Выберем из первой строки матрицы М’ незакодированный элемент 2. Построим матрицу 
, состоящую из строк матрицы М’, включающих элемент 2. В этой матрице выберем уже закодированные элементы. Получим множество B2={1}. Для каждого элемента В2 найдём множество кодов, соседних с кодом рассматриваемого состояния и ёще незанятых для кодирования. 
. Для выбора кода найдем значение весовой функции W, которая характеризует расстояние между кодами состояний, равная числу элементов памяти, изменяющих своё состояние при переходе.
Выберем тот код, для которого весовая функция минимальна. В данном случае для обоих кодов множества 
мы получили равные значения весовой функции, значит, возьмём любой код. Например, a2=101.
Отметим на карте Карно новое состояние a2.
Таблица 4.12 – Закодированные состояния на карте Карно.
| Q1\Q2Q3 | ||||
Далее вычеркиваем строки, содержащие уже закодированные состояния, и производим описанные выше действия.
, 
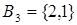a3=100
Таблица 4.13 – Закодированные состояния на карте Карно.
| Q1\Q2Q3 | ||||
Подобным образом получим a4=011.
Получение функций возбуждения блока памяти и функций выхода
Таблица 4.14 - Закодированная таблица переходов.
| А\х | ||
В качестве элементов памяти выберем JK-триггера.
Таблица 4.15 - Таблица истинности для функций возбуждения элементов памяти.
| А\х | ||||||
| 0 – | 0 – | 1 – | 0 – | 0 – | 0 – | |
| 1 – | 0 – | – 0 | 0 – | 0 – | – 1 | |
| – 0 | 0 – | – 0 | – 0 | 0 – | – 1 | |
| – 1 | 0 – | 1 – | – 1 | 1 – | 1 – | |
| 0 – | – 1 | – 0 | 0 – | – 1 | – 1 | |
| Q1Q2Q3 | J1K1 | J2K2 | J3K3 | J1K1 | J2K2 | J3K3 |
После минимизации получим:
, 
,
, 
,
, 
Произведя минимизацию для функции выхода, получим 
.
Примеры комбинационных схем синхронных автоматов
Рисунок 4.1 - Схема автомата Мура.
При разработке комбинационной схемы использовались JK-триггера управляемые перепадом тактирующего сигнала, которые находятся в Components\Digital Primitives\ Edge Triggered Flip-Flops\JKFF. Для установки триггеров в начальное состояние на вход PREB подается единичный сигнал, а на вход CLRB – в начальный момент 0, а через малый промежуток времени 1 генератора U3.
Рисунок 4.2 - Диаграмма работы автомата Мура.
Для автомата Мили закодированная таблица переходов имеет следующий вид:
Таблица 4.16 - Закодированная таблица переходов автомата Мили.
| А\х | ||
Таблица 4.17 - Таблица истинности для функций возбуждения триггеров.
| А\х | ||||
| 0 – | 1 – | 0 – | 0 – | |
| 1 – | – 1 | 0 – | – 1 | |
| – 0 | 0 – | – 0 | 1 – | |
| – 1 | – 0 | – 1 | – 1 | |
| Q1Q2 | J1K1 | J2K2 | J1K1 | J2K2 |
, 
, 
Рисунок 4.3 - Комбинационная схема автомата Мили.
Рисунок 4.4 – Диаграммы для схемы на рисунке 4.3.
ЛАБОРАТОРНАЯ РАБОТА №5. ПРОЕКТИРОВАНИЕ И ИССЛЕДОВАНИЕ АСИНХРОННЫХ ЦИФРОВЫХ АВТОМАТОВ
Общие сведения
В отличие от синхронных автоматов, где сигналы определяются тактирующим импульсом, в асинхронных автоматах переходы между состояниями автомата вызываются непосредственным изменением входных сигналов. Таким образом, новое состояние автомата является функцией от текущего состояния и предыдущего входного сигнала. Проектирование асинхронных автоматов включает те же этапы разработки, что и синронные автоматы. Первым делом нужно построить автоматный граф, анализируя реакцию автомата на входные воздействия. При этом следует учесть, что одновременное изменение нескольких входных сигналов невозможно, поэтому переходы при таких входных сигналах не рассматриваются. Следующими этапами являются построение таблицы переходов и выходов и минимизация таблицы переходов. Затем проихводится кодирование состояний. Асинхронные автоматы можно выполнить без выделения блока памяти, используя зависимость нового состояния автомата от состояния до изменения входного сигнала и от входного сигнала. При проектировании асинхронных автоматов с выделением блока памяти в качестве элементов памяти можно использовать синхронные триггера, управляемые уровнем тактирующего сигнала. Для построения комбинационной схемы потребуется определить функции возбуждения блока памяти и функции выходного сигнала.
Рассмотрим пример построения автомата Мура и Мили с выделением и без выделения блока памяти.
Абстрактный синтез.
Спроектируем автомат, который обнаруживает последовательность 10,00,10,11. При появлении на входе автомата данной последовательности на выходе выдаётся единица, во всех других случаях 0.
Определим входной алфавит Х={ 00, 01, 11, 10 }. На выходе автомата выдаётся двоичный сигнал, следовательно, выходной алфавит Y={ 0, 1 }.
Для определения алфавита состояний и графа переходов проанализируем работу автомата.
В первый момент автомат находится в начальном состоянии a0. При прихождении сигнала 10 автомат переходит в новое состояние a1. На всех остальных сигналах (00, 01, 11) автомат будет оставаться в начальном состоянии a0, ожидая начала заданной последовательности. Автомат будет находится в состоянии a0 при неизменном входном сигнале 10, следовательно, состояние a0 является устойчивым или стабильным. Из состояния a1 при изменении сигнала на 00 автомат, отмечая прихождение правильной последовательности, перейдёт в следующее состояние a2, при сигнале 11 автомат должен установиться в начальное состояние. Сигнал 01 вообще не рассматривается, так как для получения на входе такого сигнала, когда автомат находится в состоянии a1 с входным сигналом 10, должно одновременно изменится сразу два разряда, что невозможно. Из состояния a2 под воздействием изменения сигнала на 10 предусмотрим переход в состояние а3, 01 — в начальное состояние, 11 — не рассматривается. Если автомат находится в состоянии а3 и на вход автомата подаётся сигнал 11, то это означает, что пришла заданная в условии последовательность сигналов, поэтому автомат перейдёт в состояние а4, которому соответствует единичный выходной сигнал. При изменении сигнала на 00 при состоянии а3 автомат перейдёт в начальное состояние, так как пришла не верная последовательность сигналов. Из состояния а4, в котором автомат будет находится при неизменном сигнале на входе 11, автомат перейдёт в начальное состояние под воздействием входного сигнала 01, при подаче сигнала 00 автомат перейдёт в состояние а1, так как сигнал 00 является началом заданной последовательности.
Рисунок 5.1 - Автоматный граф.
Таблица 5.1 - Первичная таблица переходов автомата:
| а0 | а0 | а0 | а0 | а1 |
| а1 | а2 | — | а0 | а1 |
| а2 | а2 | а0 | — | а3 |
| а3 | а0 | — | а4 | а3 |
| а4 | — | а0 | а4 | а1 |
Таблица 5.2 - Таблица выходов автомата Мура.
| Y | |
| а0 | |
| а1 | |
| а2 | |
| а3 | |
| а4 |
Возможно, что таблица переходов, полученная путём анализа реакции автомата на входные сигналы, будет содержать избыточное число состояний. Для исключения таких состояний производится минимизация.