Лабораторная работа N 4
Численные методы решения систем
Линейных уравнений
Порядок выполнения работы:
1 Изучить материалы по лабораторной работе. Повторить соответствующий материал лекций;
2 Выполнить индивидуальное задание;
3 Представить отчет, который включает описание задачи, методики ее решения в электронных таблицах Excel и системе Matlab и анализ результатов;
4 Защитить выполненную работу.
К решению систем линейных алгебраических уравнений (СЛУ) сводятся многие задачи анализа и синтеза физических систем различной природы: механических, гидравлических, электрических и т. п.
В общем виде система n линейных алгебраических уравнений с n неизвестными записывается так:


………………………………..

где  – неизвестные системы;
– неизвестные системы;
 – коэффициенты при неизвестных системах;
– коэффициенты при неизвестных системах;
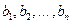 – свободные члены системы или в векторно-матричной
– свободные члены системы или в векторно-матричной
форме 
где
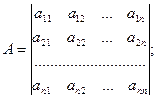


есть соответственно матрица коэффициентов, вектор-столбец свободных членов и вектор-столбец неизвестных.
Решением СЛУ называется любая совокупность чисел  , которая, будучи подставленной на место неизвестной
, которая, будучи подставленной на место неизвестной 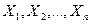 в уравнении данной системы, обращает все эти уравнения в тождества.
в уравнении данной системы, обращает все эти уравнения в тождества.
Применяемые в практике численные методы решения СЛУ делятся на две группы: точные (прямые) и приближенные (итерационные). Точными называются методы, которые в предположении, что вычисления ведутся без округления, позволяют получить точное решение за конечное число математических операций. Приближенные методы даже в предположении, что вычисления ведутся без округлений, дают решение системы лишь с заданной точностью.
Прямые методы используются при решении на ЭВМ систем небольшого порядка  . Итерационные методы целесообразно применять для систем высокого порядка
. Итерационные методы целесообразно применять для систем высокого порядка  .
.
На практике наиболее широко из прямых методов для решения СЛУ используется метод Гаусса с выбором главного элемента. Суть метода состоит в приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнения системы. Сначала с помощью первого уравнения исключается  из всех последующих уравнений системы. Затем с помощью второго уравнения исключается
из всех последующих уравнений системы. Затем с помощью второго уравнения исключается  из третьего и всех последующих уравнений. Этот процесс называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n -го) уравнения не останется лишь один член с неизвестным
из третьего и всех последующих уравнений. Этот процесс называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n -го) уравнения не останется лишь один член с неизвестным  , т. е. матрица системы будет приведена к треугольному виду. Обратным ходом метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим единственное неизвестное
, т. е. матрица системы будет приведена к треугольному виду. Обратным ходом метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим единственное неизвестное  . Далее, используя это значение, из предыдущего уравнения вычисляем
. Далее, используя это значение, из предыдущего уравнения вычисляем  и т. д. Последним найдём
и т. д. Последним найдём  из первого уравнения.
из первого уравнения.
Рассмотрим применение метода Гаусса для системы:



Для исключения  из второго уравнения прибавим к нему первое, умноженное на
из второго уравнения прибавим к нему первое, умноженное на  . Затем, умножив первое уравнение на
. Затем, умножив первое уравнение на  и прибавив результат к третьему уравнению, также исключим из него
и прибавив результат к третьему уравнению, также исключим из него  . Получим эквивалентную систему уравнений вида:
. Получим эквивалентную систему уравнений вида:

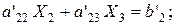
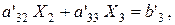
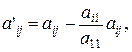

 ;
;


Теперь из третьего уравнения полученной системы нужно исключить  . Для этого умножим второе уравнение на
. Для этого умножим второе уравнение на  и прибавим результат к третьему. Получим:
и прибавим результат к третьему. Получим:


 ,
,



Т. о. матрица СЛУ имеет треугольный вид. На этом заканчивается прямой ход метода Гаусса.
Заметим, что в процессе исключения неизвестных приходится выполнять операции деления на коэффициенты  ,
,  и т. д. Поэтому они должны быть отличными от нуля: в противном случае необходимо соответственным образом переставить уравнения системы, т. е. провести выбор главного элемента. Суть этого выбора заключается в том, что из столбца коэффициентов уравнений системы, в которых не проведено очередное исключение неизвестных выбирают наибольший по модулю и перестанавливают эти уравнения так, чтобы этот коэффициент оказался на месте элемента главной диагонали матрицы системы. Обратный ход начинается с решения третьего уравнения системы:
и т. д. Поэтому они должны быть отличными от нуля: в противном случае необходимо соответственным образом переставить уравнения системы, т. е. провести выбор главного элемента. Суть этого выбора заключается в том, что из столбца коэффициентов уравнений системы, в которых не проведено очередное исключение неизвестных выбирают наибольший по модулю и перестанавливают эти уравнения так, чтобы этот коэффициент оказался на месте элемента главной диагонали матрицы системы. Обратный ход начинается с решения третьего уравнения системы:
 .
.
Используя это значение, можно найти  из второго уравнения, а затем
из второго уравнения, а затем  из первого:
из первого:


Аналогично строится вычислительный алгоритм для СЛУ с произвольным числом уравнений.
Метод прогонки – является модификацией метода Гаусса для частного случая разреженных систем – системы уравнений с трех диагональной матрицей. Такие системы получаются при моделировании некоторых инженерных задач, а также при численном решении дифференциальных уравнений на краевую задачу.
Одним из самых распространённых итерационных методов решения СЛУ, отличающийся простотой и лёгкостью программирования, является метод Гаусса-Зейделя. Проиллюстрируем этот метод на примере решения той же СЛУ, что и метод Гаусса. Предположим, что диагональные элементы  отличные от нуля (в противном случае можно переставить уравнения). Выразим неизвестные
отличные от нуля (в противном случае можно переставить уравнения). Выразим неизвестные  и
и  соответственно из первого, второго и третьего уравнения системы:
соответственно из первого, второго и третьего уравнения системы:



Зададим некоторые начальные (нулевые) приближения значений неизвестных:  . Подставляя эти значения в правую часть предыдущих выражений, получаем новое (первое) приближение для
. Подставляя эти значения в правую часть предыдущих выражений, получаем новое (первое) приближение для  :
:

Используя это значение для  и приближение
и приближение 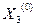 для
для  , находим новое приближение для
, находим новое приближение для  :
:

И, наконец, используя вычисленные значения  ,
,  , находим первое приближение для
, находим первое приближение для  :
:

Далее итерационный процесс продолжается по рекуррентным формулам:


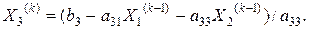
Итерационный процесс продолжается до тех пор, пока значения  не станут близкими с заданной погрешностью к значениям
не станут близкими с заданной погрешностью к значениям  .
.
Задание
Разработать ММ, блок-схему алгоритма и программу на алгоритмическом языке Pascal или Basic, в системе Matlab и в электронных таблицах для расчёта токов и напряжения в ветвях линейной электрической цепи постоянного тока, рассчитать мощность, выделяемую на резисторах. Исходные данные выбираются по заданному варианту (таблица 11).
Таблица 11 – Пример задания
| № ветви | Начало – конец | Сопротивления, Ом | Источники | |
| эдс, В | тока, А | |||
| 2–4 4–3 3-1 1-5 5-6 6-2 3-2 4-5 |
Определить напряжение  .
.
Методические указания к выполнению задания
Строим расчётную электрическую схему, которая, как очевидно, имеет 6 узлов, 8 ветвей (рисунок 8), при этом источники ЭДС и тока направляются от начала к концу ветвей и, кроме того, источники ЭДС включаются последовательно с сопротивлениями этих ветвей, а источники тока параллельно этим ветвям.
На листе бумаги отмечаем шесть узлов и между ними рисуем электрические элементы согласно таблице 11. в результате получим электрическую схему, приведенную на рисунке 8.
Очевидно, что предварительный вид электрической схемы недостаточно наглядный. Для более наглядного ее представления необходимо некоторые узлы поменять местами. В данном случае меняются местами узлы 1 и 6, а также 4 и 5. окончательный вид схемы представлен на рисунке 9. во всех ветвях схемы наметим произвольно направления токов.
| R1=650 Ом R2=510 Ом R3=130 Ом R4=340 Ом R5=420 Ом R6=240 Ом R7=430 Ом R8=310 Ом E1=100 B E2=300 B Iт=2 А Iт=4 А |
Рисунок 8 – Расчетная электрическая схема
 |
Изобразим расчетную схему в более наглядном для расчета виде (рисунок 9) и наметим произвольно направление токов во всех ветвях.
Рисунок 9 – Расчетная электрическая схема
Расчёт цепи проводим методом контурных токов. Составляем уравнения по 2-му закону Кирхгофа для контурных токов:
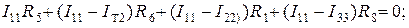


Перегруппировав слагаемые в этих уравнениях, и сделав соответствующие преобразования, получим уравнения для определения контурных токов: 




Подставляя заданные числовые значения источников ЭДС, тока и сопротивления, получим (не обязательно – результат будет в Excel):

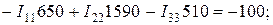

Решив полученную систему линейных уравнений, найдём значения контурных токов  ,
,  ,
, 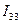 . Зная их, находим значения токов в ветвях по следующим зависимостям:
. Зная их, находим значения токов в ветвях по следующим зависимостям:
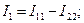



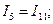


Вычислив токи, находим значения искомого напряжения  :
:

Далее определим суммарную мощность, выделяемую на резисторах:

Пример выполнения задания в пакете Excel
Таблица 12 – Исходные данные
| А | B | C | D | E | F | G | H | I | |
| R1= | I1= | ||||||||
| R2= | I2= | ||||||||
| R3= | I3= | ||||||||
| R4= | I4= | ||||||||
| R5= | I5= | ||||||||
| R6= | I6= | ||||||||
| R7= | I7= | ||||||||
| R8= | I8= | ||||||||
| E1= | U64= | ||||||||
| E2= | Psum= | ||||||||
| It1= | |||||||||
| It2= |
| C1) =B5+B6+B1+B8 D1) =-B1 E1) =-B8 C2) =-B1 D2) =B7+B2+B1 E2) =-B2 | C3) =-B8 D3) =-B2 E3) =B3+B4+B8+B2 F1) =B12*B6 F2) =-B9 F3) =B9+B10+B11*B4 |
Выделим блок ячеек C4–E6 под обратную матрицу, введем МОБР(C1:E3) и нажмем Shift+Ctrl+Enter. Затем выделим блок ячеек G1..G3 под значения контурных токов, введем МУМНОЖ (С4: E6; F1: F3) и нажмем Shift+Ctrl+Enter.
| I1) =G1-G2 I2) =G2-G3 I3) =G3 I4) =G3-B11 I5) =G1 I6) =G1-B12 I7) =G2 I8) =G1-G3 I9) =-I5*B5-I8*B8 |
I10) =I1^2*B1+I2^2*B2+I3^2*B3+I4^2*B4+I5^2*B5+I6^2*B6+I7^2*B7+I8^2*B8
Вопросы для самопроверки
1 Понятие и примеры СЛУ.
2 Что такое матрица коэффициентов, вектора неизвестных и свободных членов СЛУ? Какие элементы матрицы коэффициентов называются диагональными?
4 Дайте классификацию методам решения СЛУ.
5 Какие методы решения СЛУ называются прямыми? В каком случае они позволяют получить точное решение СЛУ? От чего зависит количество арифметических вычислений при использовании этих методов?
6 Какие методы решения называются итерационными? Что такое итерация и от чего зависит число итераций? Можно ли с помощью этого метода получить точное решение СЛУ?
7 Из каких этапов состоит решение СЛУ методом Гаусса с выбором главного элемента и в чём сущность каждого этапа? Продемонстрируйте этот метод на конкретном примере.
8 Какая СЛУ называется треугольной, в чём её особенность и как она решается?
9.
10 Поясните суть процедуры выбора главного элемента при решении методом Гаусса с выбором главного элемента? Для чего нужна эта процедура?
11 Из каких этапов состоит решение СЛУ итерационным методом Гаусса-Зейделя?
12 В каком случае итерационный процесс называется сходящимся, а в каком – расходящимся?
