Задача 1.
Для решения задачи 1 рекомендуется учебное пособие[4] Гл. I –IV, стр.39 – 91.
Рассмотрим решение аналогичной задачи 1, взяв координаты вершины пирамиды SABC: А(-3;0;0); В(0;2;0); С(0;0;6); S(-3;4;5).
1) Длину ребра АВ находим по формуле:
2) Угол между рёбрами 
найдём по формуле косинуса угла между векторами 
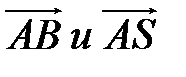, координаты которых определяются так:
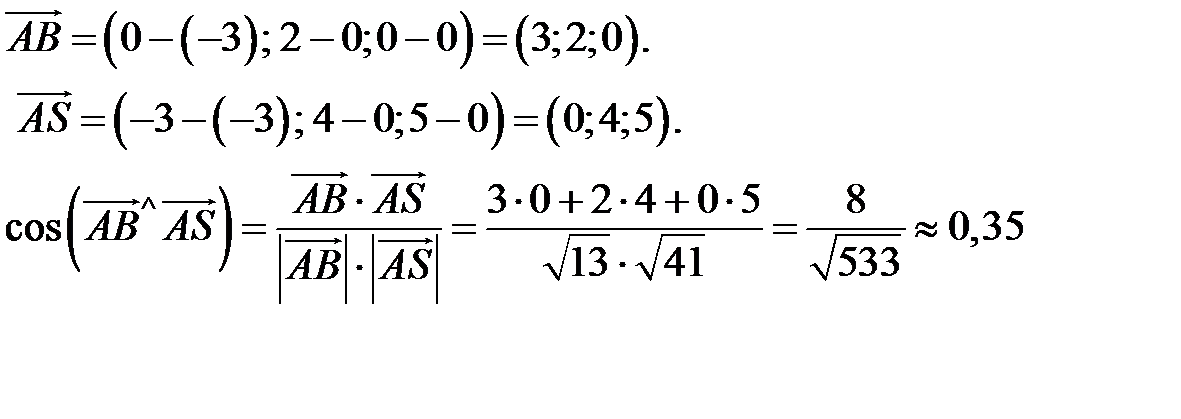
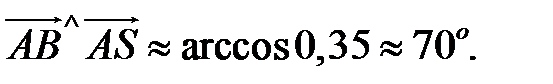
α
φ
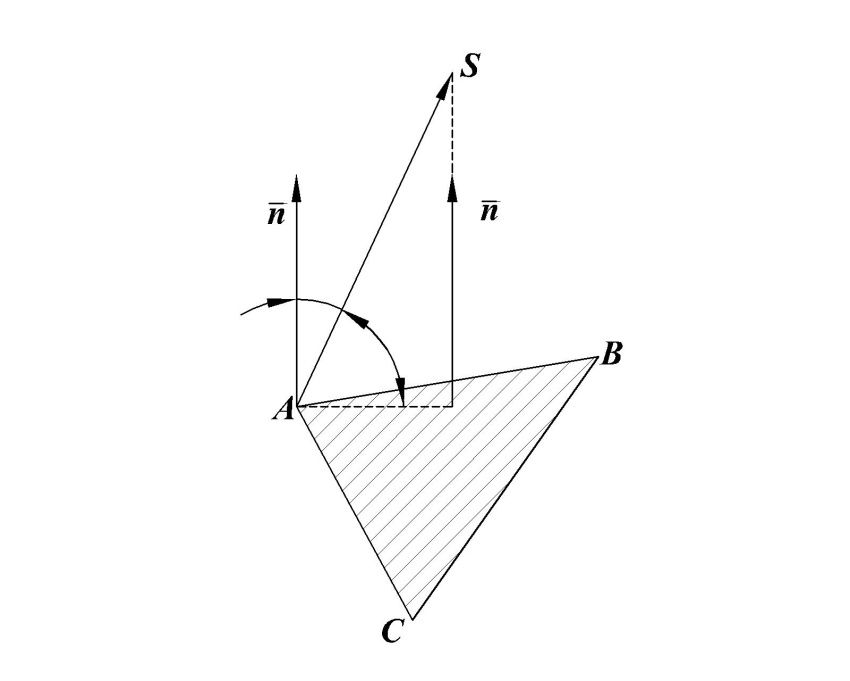
Для решения задания 3) целесообразно сначала выполнить задание 7). Уравнение плоскости(ABC) составим по формуле
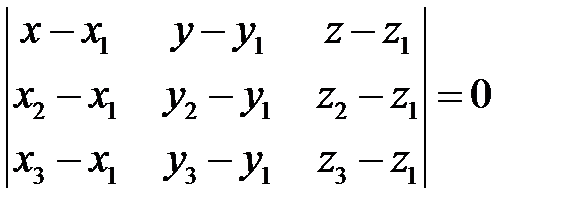
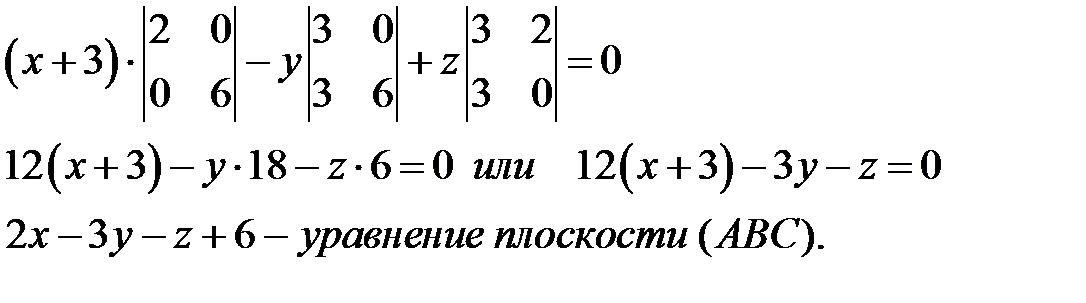
Нормальный вектор этой плоскости
4) Площадь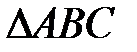 
определяем с помощью векторного произведения:
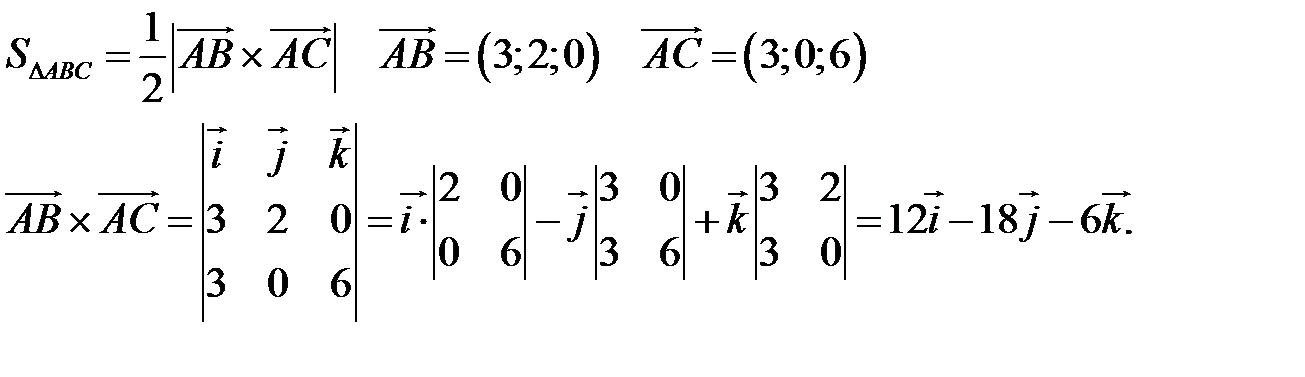
5) Объём пирамидыSABC находится через вычисление смешанного произведения векторов 
Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Решите самостоятельно.
6) Уравнение прямой (АВ) находим по формуле:
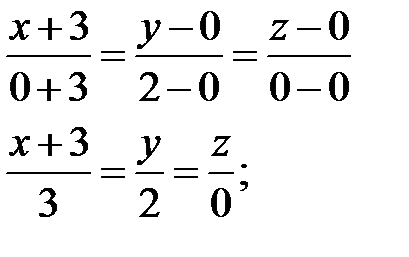
Канонические уравнения прямой, вектор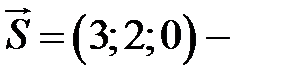 
направляющий вектор прямой 
.
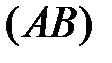8) Для определения проекции вершины 
на плоскость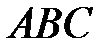 
выполняютсяследующие действия:
а) составляется уравнение высоты пирамиды (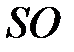
).
б) находится точка пересечения высоты и основания 
как решение системы, содержащей уравнение высоты и уравнение плоскости (АВС).
Решение: Вектор нормали 
или 
плоскости (АВС) будет направляющим вектором для высоты – прямой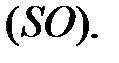 
Ее каноническое уравнение имеем вид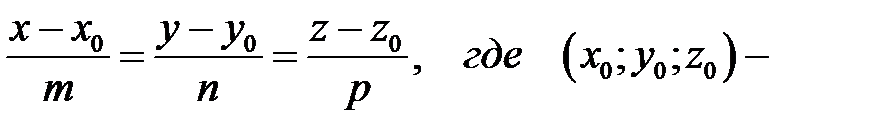 
координатывершины 
, т.е.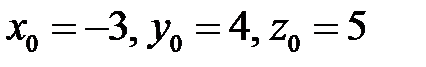 
Имеем
.
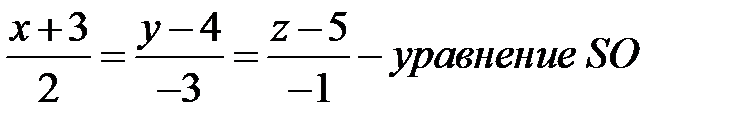Система 
решается подстановкой
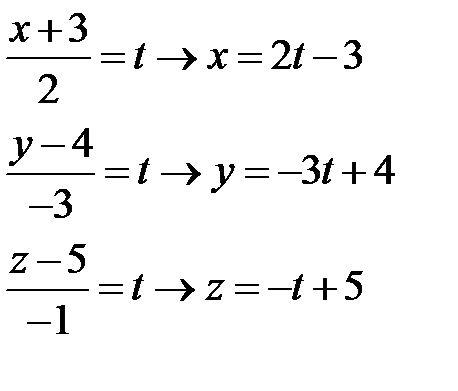
Подставив данные x, y, z во второе уравнение, найдём значение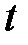 
, а следовательно значения 
Точка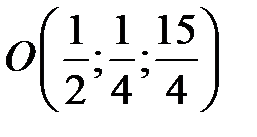 
- проекция точки 
на плоскость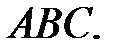 
10) Длину высоты 
пирамиды можно найти по формуле 
или по формуле расстояния от точки до плоскости – что более удобно:
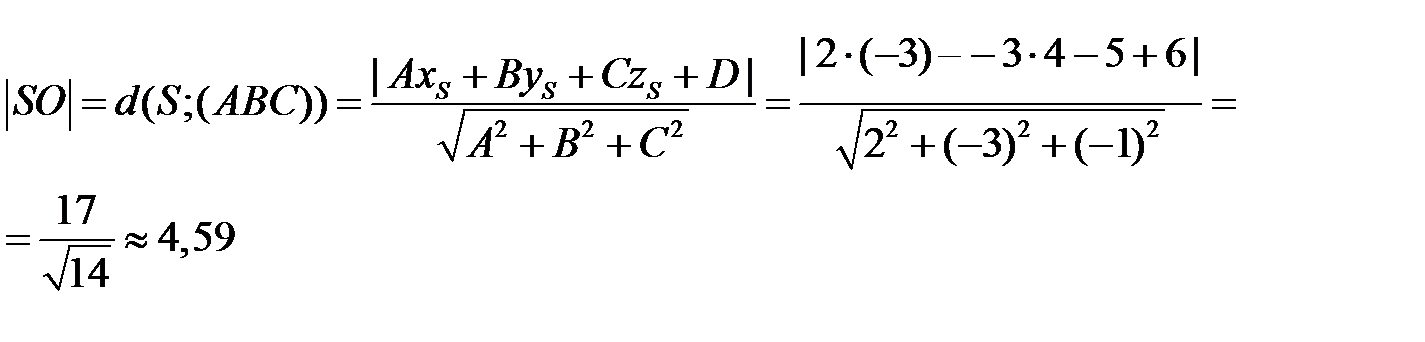
Задача 2.
Дана система линейных уравнений
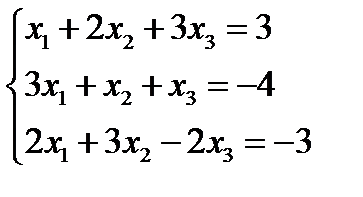
Решить систему а) матричным методом, б) методом Крамера, в) методом Гаусса.
а) данной системе соответствует матричное уравнение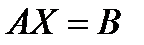 
, которое решается по формуле: 
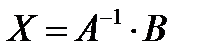. Матрицы имеют вид:
Находим обратную матрицу
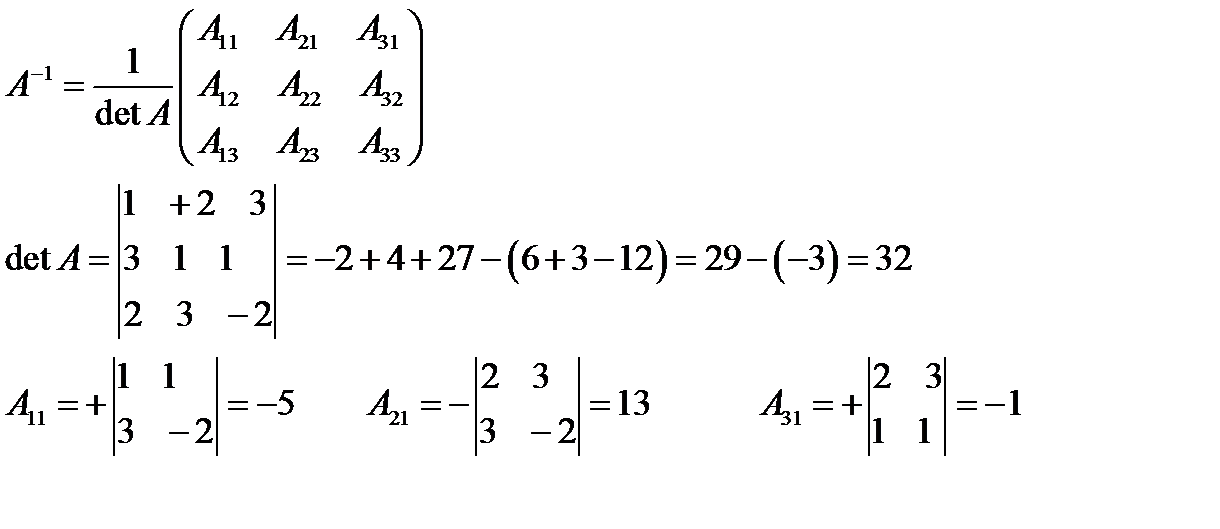
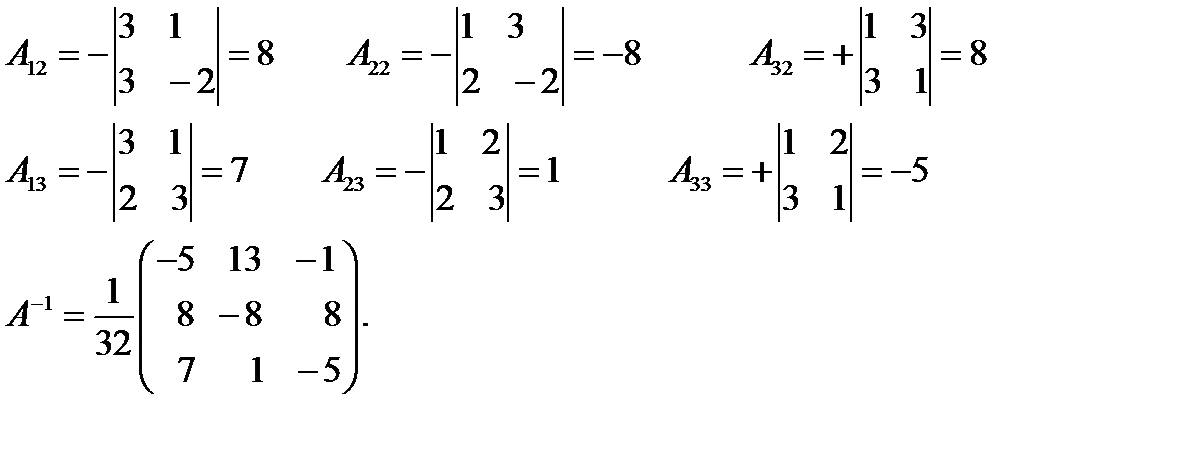
Находим матрицу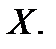 
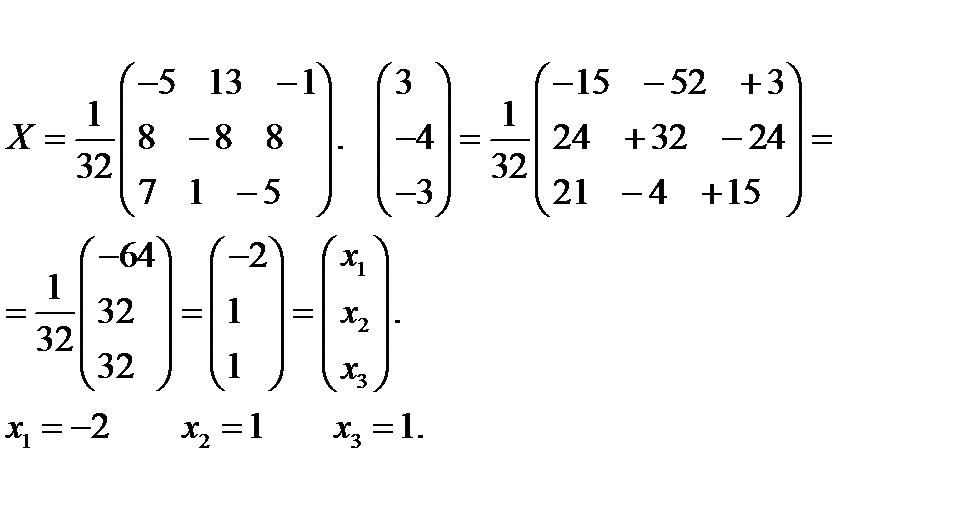
б)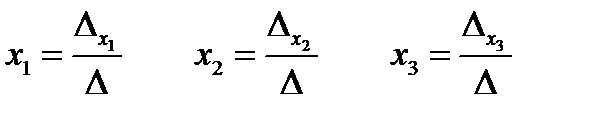 
- формулы Крамера. Вычислим все определители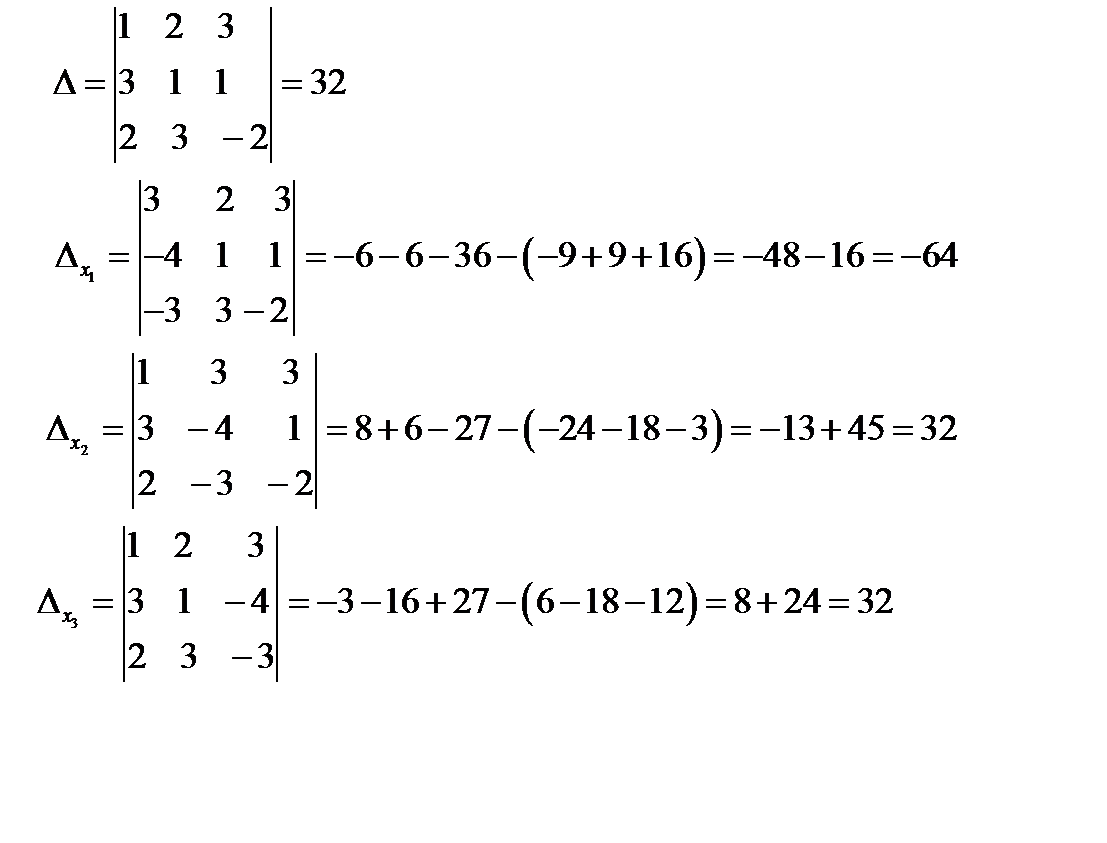 
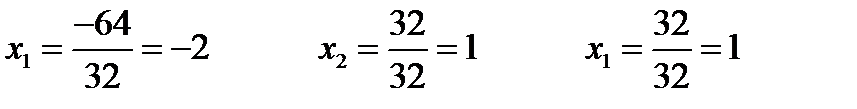
в) Метод Гаусса.
Составим расширенную матрицу 
системы и приведем ее к треугольному виду с помощью элементарных преобразований.
Составим систему соответствующую полученной треугольной матрице и решаем ее снизу вверх.
Итак: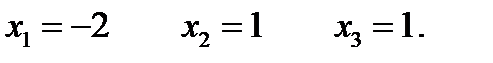 
Задача 3.
Дано комплексное число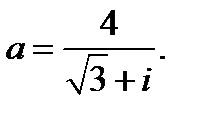 
Записать число 
в геометрической и тригонометрической формах и найти все корни уравнения 
Рекомендуемая литература: Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. II, гл.III, §7, стр.97 – 101.
Найдём алгебраическую форму комплексного числа
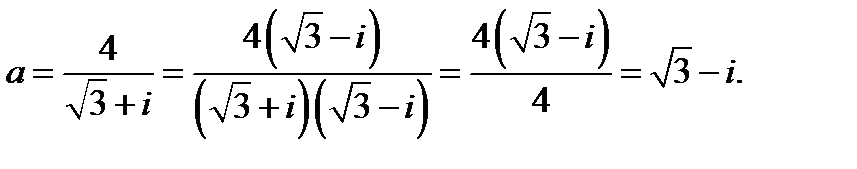
Тригонометрическая форма комплексного числа 
определится по формуле 
.
Изобразив число на плоскости, найдём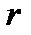 
и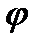 
. 
-1 
Итак, число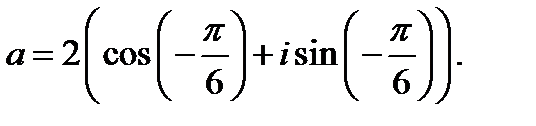 
Найдём корни уравнения 
вычислим по формуле Муавра
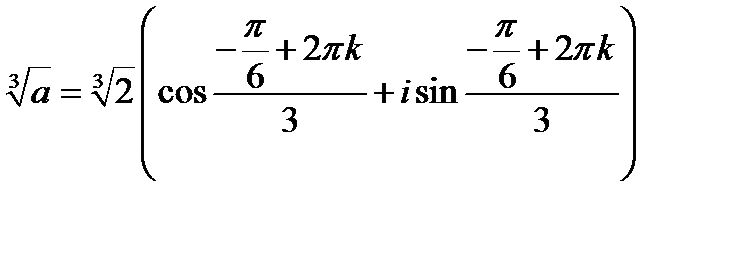
Задача 4.
Вычислить пределы:
а)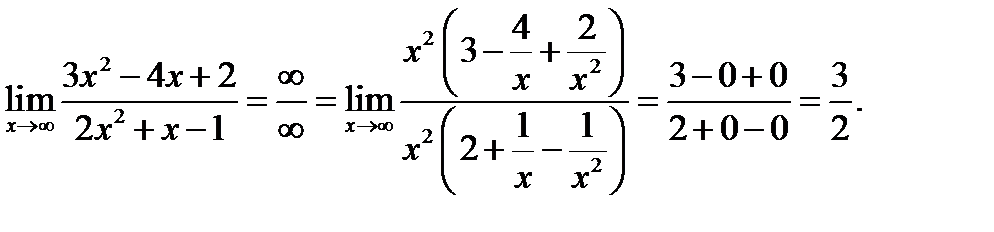 
За скобку выносили наивысшую степень х в числителя и знаменателя.
б) 
Для «раскрытия» неопределённости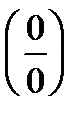 
требуется числитель и знаменатель разложить на множители.
в)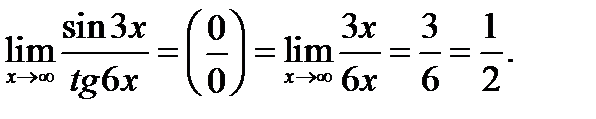 
В данном случае для исключения неопределённости 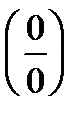использованы эквивалентные бесконечно малые,например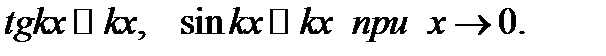 
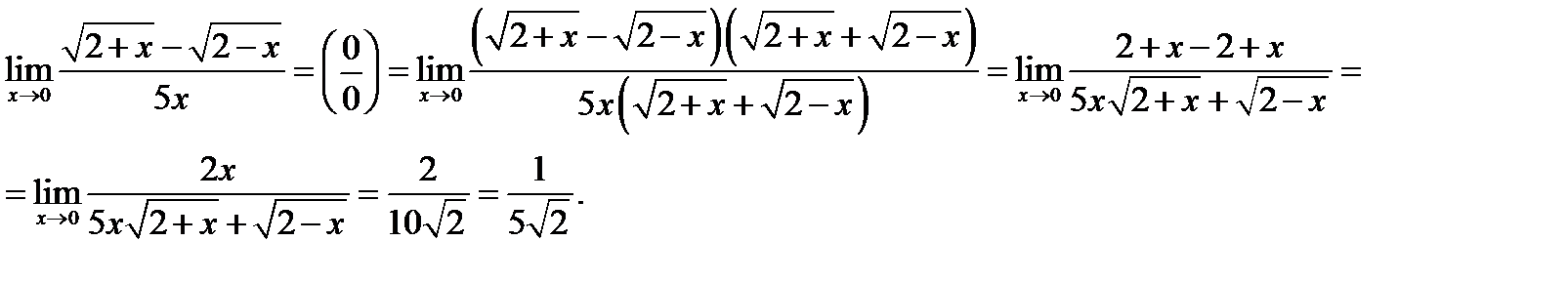г) Числитель и знаменатель умножаем на выражение, сопряжённое числителю
Для вычисления предела использован 2-ой замечатьльный предел.
Задача 5.
Найти производные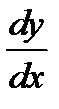 
следующих функций:
а) 
б) 
;
в) 
г)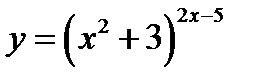 
;
д) 
.
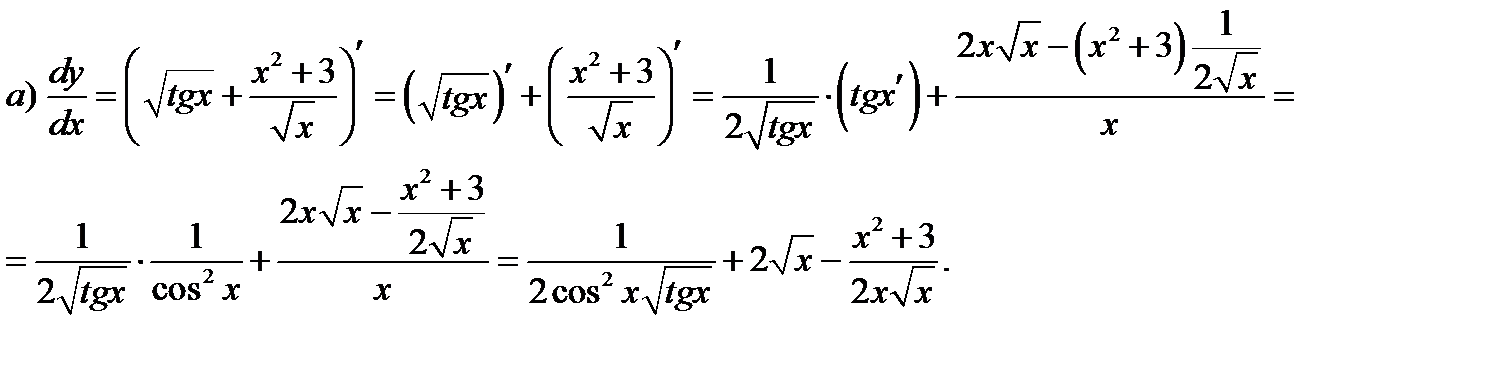
б)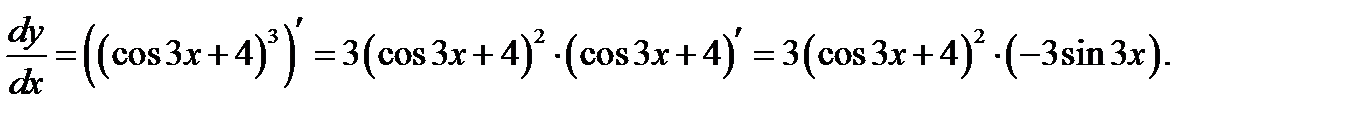 
в) 
г)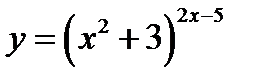 
Прологарифмируем обе части равенства
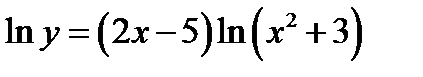
Продифференцируем обе части равенства
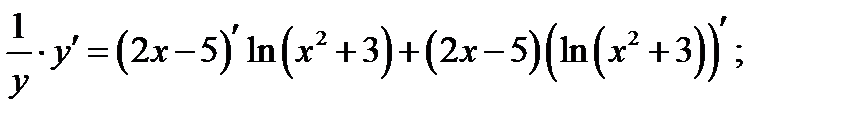
д)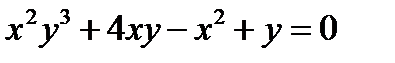 
Функция 
задана неявно. Учитываем, что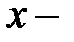 
аргумент, 
функция.
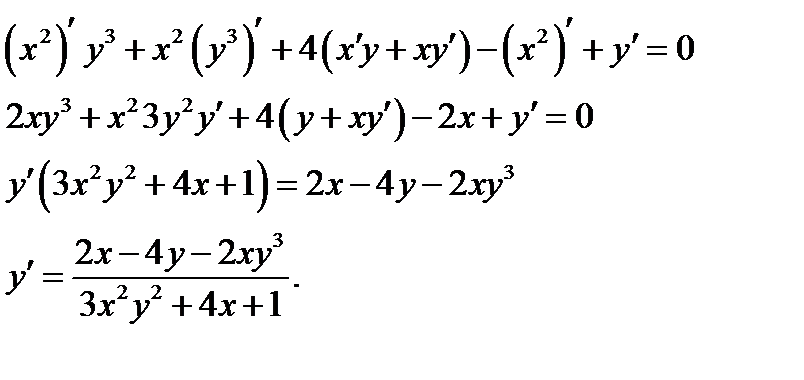
Задача 6.
Найти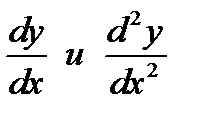 
функций:
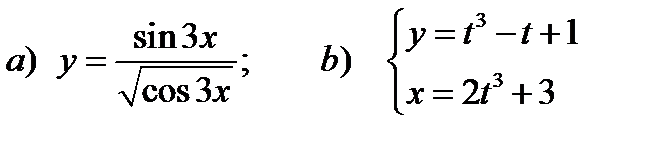
Решение:
а) 
б)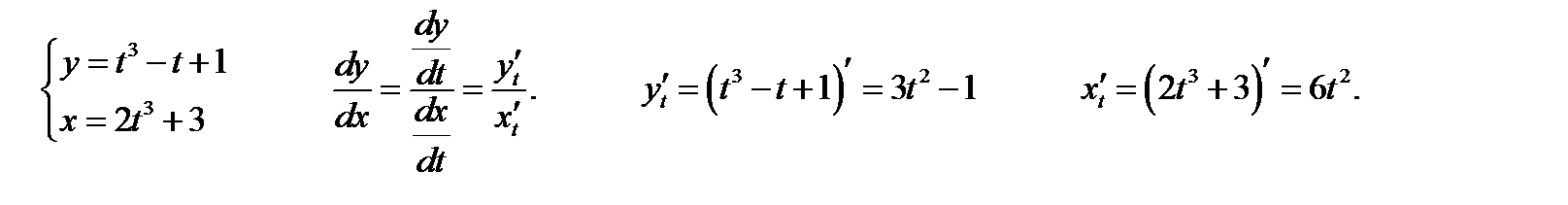 
Задача 7.
Исследовать методами дифференциального исчисления функцию и построить её график.
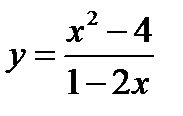
Решение. Рассмотрим свойства функции:
1. Область определения: 
2. Чётностьь, нечётность функции: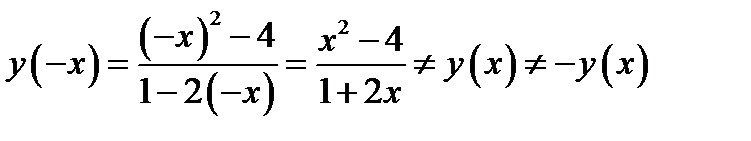 
Функция общего вида.
3. Асимптоты.
а) Так как 
, и:
то прямая 
является вертикальной асимптотой
б)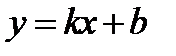 
– наклонная асимптота при 
.
Найдём 
Найдём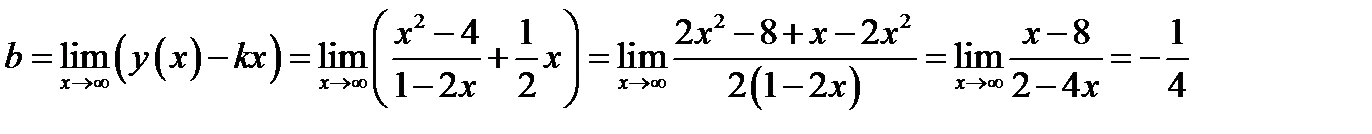 
– уравнение наклонной асимптотыпри .
4. Найдём точки экстремума и интервалы монотонности функции:
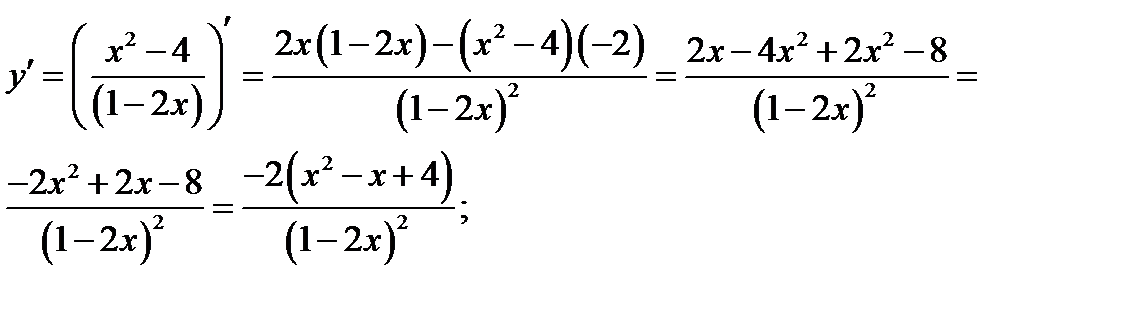
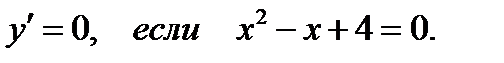
Так как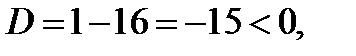 
то действительных корней нет, значит, нет и точек экстремума.
Производная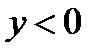 
на всей области определения, значит функция
убывает.
5. Точки пересечения с координатными осями
а) с осью 
при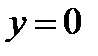 
,
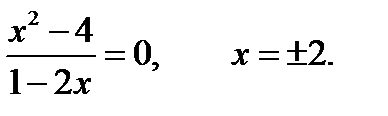б) с осью 
при 
.
Используя исследование функции, строим график (схематично).
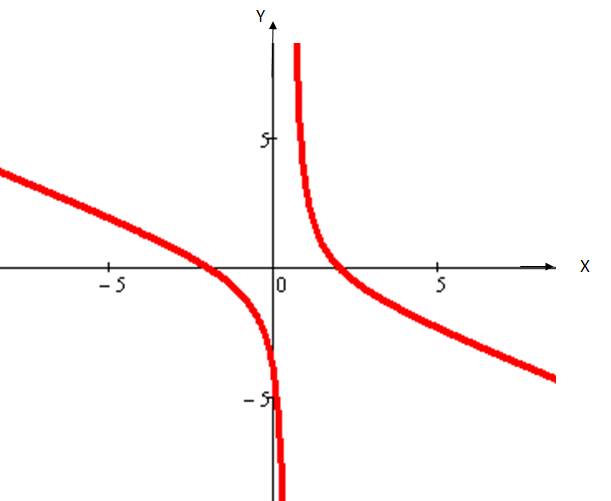
Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.
Литература
Основная литература
1. Шипачев В. С. Высшая математика. Базовый курс: учебник и практикум для бакалавров [Гриф Минобразования РФ] / В. С. Шипачев; под ред. А. Н. Тихонова. - 8-е изд., перераб. и доп. - Москва: Юрайт, 2015. - 447 с.
2. Шипачев В. С. Высшая математика. Полный курс: учебник для акад. бакалавриата [Гриф УМО] / В. С. Шипачев; под ред. А. Н. Тихонова. - 4-е изд., испр. и доп. - Москва: Юрайт, 2015. - 608 с
3. Сборник индивидуальных заданий по математике для технических высших учебных заведений: учебное пособие для вузов [Гриф Минобразования РФ]. Ч. 1: Аналитическая геометрия. Пределы и ряды. Функции и производные. Линейная и векторная алгебра. Интегрирование. Теория поля / [А. И. Архангельский и др.]; под ред. В. Б. Миносцева, Е. А. Пушкаря. - 2-е изд., испр. - Санкт-Петербург; Москва; Краснодар: Лань, 2013. - 601 с.
4. Данко П.Е., Попов А.Г., Кожевникова Т..Я. Высшая математика в упражнениях и задачах. [Текст] / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. В 2 ч. – М.: Высшая школа, 2007. – 304+415c.
Дополнительная литература
1. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. [Текст] / Б.П. Демидович, В.А. Кудрявцев. – М.: ООО "Изд. Астрель", 2001.- 437с.
2. Курс математики для технических высших учебных заведений [Электронный ресурс]: учебное пособие для вузов [Гриф УМО]. Ч. 4: Теория вероятностей и математическая статистика / Н. А. Берков [и др.]; под ред. Е. А. Пушкаря, В. Б. Миносцева. - 2-е изд., испр. - Электрон. текстовые дан. - Санкт-Петербург; Москва; Краснодар: Лань, 2013. - 304 с.
3. Курс математики для технических высших учебных заведений [Электронный ресурс]: учебное пособие для вузов [Гриф Минобразования РФ]. Ч. 3: Дифференциальные уравнения. Уравнения математической физики. Теория оптимизации / Н. А. Берков [и др.]; под ред. В. Б. Миносцева, Е. А. Пушкаря. - 2-е изд., испр. - Электрон. текстовые дан. - Санкт-Петербург; Москва; Краснодар: Лань, 2013. - 513 с.
4. Курс математики для технических высших учебных заведений: учебное пособие для вузов [Гриф Минобразования РФ]. Ч. 1: Аналитическая геометрия. Пределы и ряды. Функции и производные. Линейная и векторная алгебра / В. Г. Зубков и др.; под ред. В. Б. Миносцева, Е. А. Пушкаря. - 2-е изд., испр. - Санкт-Петербург; Москва; Краснодар: Лань, 2013. - 542 с.
5. Ляховский В. А. Курс математики для технических высших учебных заведений: учебное пособие для вузов [Гриф УМО]. Ч. 2: Функции нескольких переменных. Интегральное исчисление. Теория поля / В. А. Ляховский, А. И. Мартыненко, В. Б. Миносцев; под ред. В. Б. Миносцева, Е. А. Пушкаря. - 2-е изд., испр. - Санкт-Петербург; Москва; Краснодар: Лань, 2013. - 428 с.
6. Пискунов Н.С. Дифференциальное и интегральное исчисления [Текст] / Н.С. Пискунов. В 2-х т. – М.: Интеграл-Пресс, 2005.- 460+510с.
ЗАДАНИЯи методические указания к выполнению