Расчеты напряженно - деформированного состояния балки
Выполнил студент гр. 6-См-1 Мельников Р. В.
Руководитель Семенов А. А.
Санкт-Петербург
Содержание
Введение……………………………………………………………………………………………………….2
1. Классификация математических моделей………………………………………………3
2. Метод Ритца………………………………………………………………………………………..……5
3. Расчеты напряженно - деформированного состояния балки………….…….7
3.1. Расчет линейно-упругой задачи для стальной балки…………….…….7
3.2. Расчет нелинейно-упругой задачи для стальной балки……….….…..9
3.3. Расчет линейно-упругой задачи для бетонной балки………….…….12
3.4. Расчет задачи ползучести для бетонной балки………………………….13
Заключение………………………………………………………………………………..……………….15
Список используемой литературы…………………………………………………………….16
Введение
С появлением электронно-вычислительных машин был разработан новый способ теоретического исследования сложных процессов, т.е. исследование естественнонаучных проблем средствами вычислительной математики.
Суть вычислительного эксперимента состоит в составлении математической модели изучаемого процесса или явления, которая представляет собой некоторые математические уравнения, затем разрабатывается вычислительный алгоритм для решения этих уравнений, составляется программа для ЭВМ и проводится расчет конкретных вариантов состояния объекта при изменении входящих в уравнение параметров. Т. о. основой изучения различных объектов является построение математической модели их функционирования.
Целью курсовой работы является разработка математических моделей деформирования элементов строительных конструкций, построение методики исследования напряженно-деформированного состояния стальной и бетонной балок.
Классификация математических моделей
Математическая модель – математическое представление реальности, один из вариантов модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе.
Процесс построения и изучения математических моделей называется математическим моделированием.
Математические модели можно классифицировать по нескольким основным признакам.
1. Статические и динамические модели
Модель называется статической, если значение выхода зависит от значения входа в один и тот же момент времени. В динамических моделях значение выхода может зависеть от всего прошлого входного процесса. Для динамических моделей предметом изучения является изменение исследуемого объекта во времени.
2. Детерминированные и вероятностные модели.
Если математическая модель включает случайные величины, подчиняющиеся статистическим законам, то она называется вероятностной или стохастической. Математическая модель, не содержащая случайных компонентов, называется детерминированной.
3. Дискретные и непрерывные модели.
Величины могу быть двух типов – дискретные, т. е. принимающие отдельные значения, допускающие естественную нумерацию, и, непрерывные, принимающие все значения из некоторого интервала. Возможный также смешанный случай, например, когда на одном интервале величина ведет себя как дискретная, а на другом – непрерывная. Подобным образом и математические модели могут быть либо дискретными, либо непрерывными, либо смешанными. Надо учитывать возможность применения либо дискретного, либо непрерывного аппаратов при построении математической модели и способа ее исследования.
4. Линейные и нелинейные модели.
Линейная зависимость одной величины от другой – это пропорциональность их приращений, т. е. зависимость вида y=ax+b, откуда получаем △y=a△x. Аналогично, определяется понятие и линейной модели. Если модель рассматривать как преобразователь, для которого каждому входу соответствует некоторый выход. Тогда модель называется линейной, если в ней выполняется принцип суперпозиции, т.е. при сложении входов складываются и выходы, при умножении входа на любое число выход умножается на то же число. Пользуясь принципом суперпозиции, нетрудно, найдя решение в каком – либо случае, построить решение в более общей ситуации. Поэтому о качественных свойствах общего случая можно судить по свойствам частного – различие между двумя решениями носит лишь количественный характер.
Одним из важнейших свойств математических моделей является их универсальность. Его сущность заключается в том, что одними и теми же математическими моделями могут описываться совершенно различные по природе процессы, т.е. одни и те же приемы и методы построения и исследования математических моделей пригодны для различных задач.
Однако решение таких задач требует интегрирования сложной системы дифференциальных уравнений в частных производных и сопряжено со значительными математическими трудностями. Поэтому при решении прямой задачи часто используют приближенные методы, например прямые методы вариационных задач (метод Ритца), а также метод конечных элементов.
Метод Ритца
Метод Ритца - прямой метод нахождения приблизительного решения краевых задач вариационного исчисления.
Метод предусматривает выбор пробной функции, которая должна минимизировать определенный функционал, в виде суперпозиций известных функций, которые удовлетворяют граничным условиям. При этом задача сводится к поиску неизвестных коэффициентов суперпозиции. Пространственный оператор в операторном уравнении, который описывает краевую задачу, должен быть линейным, симметрическим и положительно-определенным.
Метод Ритца позволяет найти неизвестные функции перемещений из условия минимума функционала полной энергии деформации.
Рассмотрим функционал энергии:
=  (1)
(1)
Требуется найти минимум функционала (3.1), т. е. найти функции u (x, y), v (x, y), w (x, y), заданные в некоторой области D = {0 ≤ x ≤ a; 0 ≤ y ≤ b }, удовлетворяющие некоторым однородным краевым условиям на границе Γ, при которых функционал (1) имеет минимальное значение. Приближенное решение поставленной задачи будем искать в виде:
u(x,y)=uN= 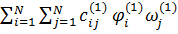 ,
,
v(x,y)=vN=  ,
,
w(x,y)=wN=  .
.
Чтобы избежать двух индексов, представим перемещения в виде:
U(x,y)=  ;
;
V(x,y)=  ;
;
W(x,y)=  . (2)
. (2)
Здесь U (I), V (I), W (I) – неизвестные числовые параметры; X 1(I), X 2(I), X 3(I)– известные аппроксимирующие функции переменной x, удовлетворяющие при x = 0, x = a заданным краевым условиям; Y 1(I), Y 2(I), Y 3(I) – известные аппроксимирующие функции переменной y, удовлетворяющие при y = 0, y = b заданным краевым условиям. Функции X 1(I) − X 3(I), Y 1(I) − Y 3(I) называются базисными функциями.
Подставляя (2) в (1) и выполняя интегрирование от известных функций, сведем функционал (1) к функции:
J=J(U(I),V(I),W(I)) (3)
параметров U (I), V (I), W (I), I =1,…, N.
Чтобы функция (3.3) имела минимум, ее частные производные по переменным U (l), V (l), W (l), l =1,.., N должны обращаться в нуль:
 (4)
(4)
Система (4) представляет собой систему линейных алгебраических уравнений, для решения которой можно применять метод Гаусса. Найденные значения параметров U (I), V (I), W (I) подставляем в разложения (2) и получаем приближенное решение поставленной задачи. Существование минимума функционалов полной энергии деформации элементов строительных конструкций (стержень, плита, оболочка) доказано.