Корреляционной зависимостью Y от Х называют функциональную зависимость условной средней 
от х.
представляет уравнение регрессии Y на Х, а 
- уравнение регрессии Х на Y.
Корреляционная зависимость может быть линейной и криволинейной. В случае линейной корреляционной зависимости уравнение прямой линии регрессии имеет вид:
, (8).
где угловой коэффициент а прямой регрессии Y на Х называется выборочным коэффициентом регрессии Y на Х и обозначается rух.
При малых выборках данные не группируются. Параметры a и b находятся по методу наименьших квадратов из системы нормальных уравнений:
(9).
где n – число наблюдаемых значений пар взаимозависимых величин.
Выборочный линейный коэффициент корреляции rВ показывает тесноту связи между Y и Х. Коэффициент корреляции находится по формуле
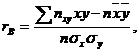(10).
Причем |rВ| £ 1, а именно:
а) если rВ = 0, то X и Y не связаны корреляционной зависимостью;
б) если |rВ| = 1, то X и Y связаны функциональной зависимостью;
в) если |rВ| < 1, то между X и Y существует корреляционная зависимость, при этом эта связь тем теснее, чем |rВ| ближе к единице.
Выборочное уравнение прямой линии регрессии Y на Х имеет вид:
(11).
Выборочное уравнение прямой линии регрессии Х на Y имеет вид:
(12).
При большом числе наблюдений признаков X и Y составляется корреляционная таблица с двумя входами, при этом одно и то же значение х наблюдается nx раз одно и то же значении y наблюдается ny раз и одна и та же пара (х; у) наблюдается nxy раз.
Лабораторная работа № 4
Задание. На основании результатов экзаменационной сессии соберите данные об успеваемости по одной дисциплине (признака Х) и по другой дисциплине (признаку Y), с помощью статистических методов изучите зависимость между этими величинами.
|
|
|
Цель работы. Овладение методами установления связи между двумя случайными величинами X и Y при большом числе наблюдений и методами определения параметров выборочного уравнения прямой линии регрессии по сгруппированным данным.
Порядок выполнения лабораторной работы:
Соберите данные о значении признака Х - успеваемость по математике и Y – успеваемость по информатике у студентов одного курса. Число студентов вычислить по формуле n = k + 20, где k – порядковый номер студента в журнале.
Примечание. Данные о значениях признаков X и Y можно выборочно взять из экзаменационных ведомостей или ведомостей рубежного контроля.
2. Полученные данные внесите в корреляционную таблицу
 yi
xi
| nx | ||||
| ny | n |
Порядок заполнения внутри таблицы поясним примером. В группе 5 студентов получили «удовлетворительно» (3) по отечественной истории и «хорошо» (4) по философии. В уголке клетки (на пересечении третьей строки и четвертого столбца) записывается значение ху, равное 12. После заполнения соответствующих клеток внутри таблицы подсчитайте n x для каждого x i и n y для каждого y i. Должно иметь место равенство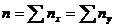 
. По виду корреляционной таблицы установите форму корреляционной связи признаков Х и Y.
3. Корреляционную таблицу дополните до расчетной таблицы и произведите необходимые вычисления.
|
|
|
 yi
| n x | n x x | n x x 2 | n xy xy | ||||
| xi | ||||||||
| n y | n | ∑n x x | ∑n x x 2 | ∑n xy xy | ||||
| n y y | ∑n y y | |||||||
| n y y 2 | ∑n y y 2 | |||||||
| n xy xy | ∑n xy xy |
4. Вычислите 
,
.
5. Найдите sх и sу по формулам:
, 
.
6. По формуле (10) вычислите выборочный коэффициент корреляции rВ и установите по его величине степень тесноты связи.
7. Подставьте найденные величины в уравнение 11 прямой линии регрессии Y на Х.
8. Подставьте найденные величины в уравнение 12 прямой линии регрессии Х на Y.
9. Постройте линии на графике и убедитесь, что обе линии походят через точку (
).
Вопросы самоконтроля и самопроверки
Способы отбора статистических данных.
Какие способы отбора применяются на практике?
Полигон и гистограмма.
Формулы для вычисления выборочных числовых характеристик.
Как найти доверительный интервал для математического ожидания нормально распределенной случайной величины (при известном s; при неизвестном s)?
Как найти доверительный интервал для среднего квадратического отклонения нормально распределенной случайной величины?
Какая зависимость между величинами называется корреляционной?
Что такое уравнение линии регрессии?
|
|
|
Что называется выборочным коэффициентом корреляции?
Сформулируйте свойства выборочного коэффициента корреляции.
Список рекомендуемой литературы
Основная:
1. Гмурман В.Е. Теория вероятностей и математическая статистика – М.: Высшая школа. 2003
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М. -: Высшая школа, 2003.
Дополнительная:
1. Виленкин Н.Я., Потапов В.Г. Задачник – практикум по теории вероятностей с элементами комбинаторики и математической статистики. М.: Просвещение, 1979.
2. Общие требования и правила оформления выпускных квалификацио 
нных работ, курсовых проектов (работ) отчетов по РГЗ, по УИРС, по производственной практике и рефератов. Оренбургский государственный университет, 2000.
