Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω:

ЗАДАЧА. Мишень имеет форму окружности радиуса 4. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены
Решение:
 Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем:
Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем: 
Ответ: 0,5
6. Условная вероятность. Теорема умножения вероятностей.
Во многих задачах приходится находить вероятность совмещения событий А и В, если известны вероятности событий А и В.
Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:
| 1-я монета | 2-я монета | |
| 1-й исход | герб | герб |
| 2-й исход | герб | надпись |
| 3-й исход | надпись | герб |
| 4-й исход | надпись | надпись |
Таким образом, P(герб,герб)=1/4.
Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:
| 1-я монета | 2-я монета | |
| 1-й исход | герб | герб |
| 2-й исход | герб | надпись |
При этом только один из исходов благоприятствует событию (герб, герб). Поэтому при сделанных предположениях Р(герб,герб)=1/2. Обозначим через А появление двух гербов, а через В — появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что событие B произошло.
Новую вероятность события А, в предположении, что произошло событие B, будем обозначать PB(А).
Таким образом, Р(A)=1/4; PB(А)=1/2
Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
| P(AB)=P(A)PA(B) | (4) |
Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2,..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает
 ;
;  ;
; 
Таким образом,

Поменяв местами A и B, аналогично получим

| (5) |
Из формул (4) и (5) имеем

| (6) |
Теорема умножения легко обобщается на любое, конечное число событий. Так, например, в случае трех событий A1, A2, A3 имеем *

В общем случае

| (7) |
Введем теперь следующее определение.
Два события A и B называются независимыми, если предположение о том, что произошло одно из них, не изменяет вероятность другого, т. е. если
 и и 
| (8) |
Из соотношения (6) вытекает, что из двух равенств (8) одно является следствием другого.
Пусть, например, событие A — появление герба при однократном бросании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы.
В случае независимости событий A к B формула (4) примет более простой вид:

| (9) |
т. е. вероятность совмещения двух независимых событий равна произведению вероятностей этих событий.
События А1, А2,..., Аn называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились.
Исходя из этого определения, в случае независимости событий А1, А2,..., Аn между собой в совокупности на основании формулы (7) имеем

| (10) |
Формула Бейеса
Пусть мы знаем вероятности событий А и В: Р(А) и Р(В). И пусть мы знаем условную вероятность события А по В: Р(A|B). Как найти условную вероятность P(B|A)? На этот вопрос отвечает формула Бейеса. Р(B|A)=P(A|B)·P(B)/P(A) (1) Разумеется этой формулой можно пользоваться только при условии, что Р(А)0. Формула Бейеса выводится из следующих равенств: Р(ВА)=Р(В|A)·P(A) (2) Р(AB)=Р(A|B)·P(B) (3) Р(ВА)=Р(AB) (4) так как пересечение событий В и А очевидно не зависит от порядка, в котором записаны А и В, т.е. ВА=AB. В случае Р(А)=0 принимаю обычно, что Р(В|A) есть величина неопределенная. 8.Формула полной вероятности.
Пусть имеем полную группу из n попарно непересекающихся событий  То есть
То есть
 ,
, 
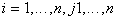 , (6)
, (6)
Пусть мы знаем условные вероятности некоторого события А по Еi: Р(А|Ei) и вероятности Р(Ei), i=1,...,n. Справедлива следующая формула полной вероятности для события А Р(А)=Р(A|E1)·P(E1)+...+P(A|En)·P(En) (7) Доказательство этой формулы вытекает из следующих равенств P(A)=P()=P(A(Ei))=P(AE1)+...+P(AEn)=Р(A|E1)·P(E1)+...+P(A|En)·P(En) (8) Из элементарной формулы Бейеса (1) и формулы полной вероятности (7) вытекает следующая более полная формула Бейеса
Р(Еi|A)=P(A|Ei)·P(Ei)/(Р(A|E1)·P(E1)+...+P(A|En)·P(En)) (9)
Полная группа событий
Несовместимые события – события, наступление которых одновременно при одном и том же опыте (испытании) невозможно. Например, выпадение двух граней кубика при одном броске невозможное событие.
Полная группа событий – совокупность однородных несовместимых событий, наступление одного из которых обязательно. Для примера с игральным кубиком полная группа событий будет выпадение каждой из шести граней.
И по классическому и по аксиоматическому определению вероятности очевидно, что вероятность наступления любого случайного события А будет равна 0<Р(А)<1. Краевые значения 0 и 1 будут определять неслучайные события – их делят на:
невозможные – (Р(А)=0 или Р(Ө)=0) – наступление которых при данных условиях невозможно
достоверные – (Р(А)=1) – наступление которых при данных условиях обязательно.
Для несовместимых событий легко определить вероятность объединения (суммы) событий. Если Аi при i Є (1, n) несовместимые события, то вероятность суммы событий Аi равна сумме их частных вероятностей.
Р(А1+А2+,…,+Аn) = Р(А1)+Р(А2)+…+Р(Аn)
Независимость событий
Событие А называется независимым от события В, если наступление события А не оказывает никакого влияния на вероятность наступления события В.Вероятность одновременного наступления двух независимых событий равна произведению вероятностей этих событий.
Р(АВ) = Р(А)*Р(В) или Р(А1,А2,…,Аn) = Р(А1)*Р(А2)*…*Р(Аn)
Учитывая независимость событий и возможность появления двух событий одновременно тогда вероятность суммы двух независимых событий А и В более точно находят следующим образом:
Р(А+В) = Р(А) + Р(В) – Р(АВ),
где Р(АВ) – вероятность их одновременного появления
Условность событий
Безусловные события рассматриваются вне конкретных условий и обозначаются просто буквами А,В,С и т.д.
Условные события – рассматриваются при наступлении других событий. Они обозначаются например А/В – событие А при условии наступления события В и т.д.
Условную вероятность события А при наступлении события В находят следующим образом:
Р(А/В)=Р(АВ)/Р(В), если Р(В) ≠0
С помощью условных и безусловных вероятностей можно корректно определить зависимость или независимость событий.
События А,В и С называют независимыми если их безусловные вероятности равны их условным вероятностям:
Р(А)=Р(А/В)=Р(А/С)=Р(А/ВС)
Р(В)=Р(В/А)=Р(В/С)=Р(В/АС)
Р(С)=Р(С/А)=Р(С/В)=Р(С/АВ)
Это так называемое условие независимости событий. Если это условие нарушается, то события зависимы. Чем больше различия, тем сильнее зависимость.
Если рассмотреть вероятность совмещения (произведения) двух событий с учетом условности, то есть если принять что событие А наступает при условии наступления события В, то вероятность совмещения можно записать двумя способами:
Р(АВ)=Р(А)*Р(В/А)
Р(АВ)=Р(В)*Р(А/В)
Если брать три события, то количество способов, которыми можно записать вероятность их совмещения возрастает до двенадцати и т.д.