Лекции по аналитической геометрии
Краткий конспект
Литература:
1. Ильин В.А., Позняк Э.Г. «Аналитическая геометрия»
2. Ильин В.А.,Ким Г.Д. «Линейная алгебра и аналитическая геометрия»
3. Беклемишев Д.В. «Курс аналитической геометрии и линейной алгебры»
4. Веселов А.П., Троицкий Е.В. «Лекции по аналитической геометрии»
5. Цубербиллер О.Н. «Задачи и упражнения по аналитической геометрии»
ВЕКТОРНАЯ АЛГЕБРА
О. Упорядоченную пару точек (А,В) на прямой будем называть направленным отрезком или фиксированным вектором (Ф.В.) и обозначать  . Вектор
. Вектор  будем называть нулевым.
будем называть нулевым.
О. Расстояние между точками А и В будем называть длиной (модулем) Ф.В. и обозначать  .
.
О. Ф.В. 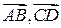 будем называть коллинеарными, если они расположены на параллельных прямых, либо хотя один из них нулевой. Обозначение:
будем называть коллинеарными, если они расположены на параллельных прямых, либо хотя один из них нулевой. Обозначение: 
О. Коллинеарные Ф.В. 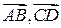 будем называть сонаправленными или прямоколлинерными, если лучи [AB) и [CD) имеют одинаковое направление, и противоположно направленными или антиколлинеарными, если лучи [AB) и [CD) имеют противоположное направление. Обозначение:
будем называть сонаправленными или прямоколлинерными, если лучи [AB) и [CD) имеют одинаковое направление, и противоположно направленными или антиколлинеарными, если лучи [AB) и [CD) имеют противоположное направление. Обозначение:  и
и  соответственно.
соответственно.
О. Векторы  называются компланарными, если они расположены в параллельных плоскостях.
называются компланарными, если они расположены в параллельных плоскостях.
О. Два Ф.В. 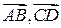 называютя равными, если они сонаправлены и имеют одинаковую длину. Обозначение:
называютя равными, если они сонаправлены и имеют одинаковую длину. Обозначение: 
Множество всех Ф.В. можно разбить на классы эквивалентности равных между собой Ф.В.. Класс эквивалентности Ф.В. называется свободным вектором или просто вектором. Обозначение:  Таким образом, вектор
Таким образом, вектор 
 состоит из всех Ф.В., равных
состоит из всех Ф.В., равных  . Обычно вместо символа
. Обычно вместо символа 
 используется символ
используется символ 
 , который в зависимости от контекста читается как «вектор
, который в зависимости от контекста читается как «вектор  , порожденный Ф.В.
, порожденный Ф.В.  » или «вектор
» или «вектор  , отложенный от точки А».
, отложенный от точки А».
Векторы называются коллинеарными (компланарными), если коллинеарны
(компланарны) порождающие их вектора.
Линейные операции над векторами
Сложение векторов Сумма векторов 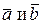 определяется следующим образом. Отложим вектор
определяется следующим образом. Отложим вектор  отпроизвольной точки А, пусть В – конец этого вектора, т.е.
отпроизвольной точки А, пусть В – конец этого вектора, т.е. 
 . Затем отложим вектор
. Затем отложим вектор  от точки В, пусть
от точки В, пусть 
 . Суммой
. Суммой  векторов
векторов  называется вектор, порожденный Ф.В.
называется вектор, порожденный Ф.В.  .
.
Это правило сложения векторов называется правилом треугольника. Очевидно, что этот же вектор  для неколлинеарных векторов
для неколлинеарных векторов  может быть получен как диагональ параллелограмма, построенного на векторах
может быть получен как диагональ параллелограмма, построенного на векторах  .
.
Вектор  называется противоположным к вектору
называется противоположным к вектору 
 и обозначается
и обозначается  .
.
Разность векторов  называется вектор
называется вектор  такой, что
такой, что  . Обозначение:
. Обозначение: 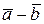 .
.
Умножение вектора на число. Произведение вектора  на число α – вектор α
на число α – вектор α  , удовлетворяющий условиям:
, удовлетворяющий условиям:
1)  2)
2) 
Свойства линейных операций:
 .
.
Линейная зависимость векторов
Пусть  - множество векторов и
- множество векторов и  -действительные числа.
-действительные числа.  - линейная комбинация векторов
- линейная комбинация векторов  ,
,
 - коэффициенты линейной комбинации.
- коэффициенты линейной комбинации.
О. Множество векторов  называется линейно зависимым, если существует ненулевой набор чисел
называется линейно зависимым, если существует ненулевой набор чисел  , при котором
, при котором 
Т1 (Критерий линейной зависимости)
Множество векторов линейно зависимо тогда и только тогда, когда хотя бы один из векторов линейно выражается через остальные вектора.
Т2 (О линейно зависимой подсистеме)
Если множество векторов содержит линейно зависимое подмножество, то оно линейно зависимо.
Следствия.
1) Множество векторов, содержащее нуль-вектор линейно зависимо.
2) Если множество векторов линейно независимо, то всякое его подмножество линейно зависимо.
Т3 (О линейной зависимости 2-х векторов)
Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Лемма1 (О разложении вектора в плоскости)
Пусть векторы  компланарны и
компланарны и  . Тогда существует единственный набор чисел
. Тогда существует единственный набор чисел 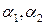 такой, что
такой, что 
Z. Упорядоченная тройка неколлинеарных векторов  - базис в плоскости этих векторов и всякий компланарный с ними вектор можно разложить по базисным векторам:
- базис в плоскости этих векторов и всякий компланарный с ними вектор можно разложить по базисным векторам:  , коэффициенты разложения
, коэффициенты разложения 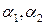 называются координатами вектора
называются координатами вектора  в базисе
в базисе  .
.
Т4 (О линейной зависимости 3-х векторов)
Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Лемма2 (О разложении вектора в пространстве)
Пусть векторы  некомпланарны. Тогда для любого вектора
некомпланарны. Тогда для любого вектора  найдется единственный набор чисел
найдется единственный набор чисел  такой, что
такой, что  .
.
Z. Упорядоченная тройка некомпланарных векторов  - базис в пространстве и всякий вектор можно разложить по базисным векторам:
- базис в пространстве и всякий вектор можно разложить по базисным векторам:  , коэффициенты разложения
, коэффициенты разложения  называются координатами вектора
называются координатами вектора  в базисе
в базисе  .
.
Базис называется ортогональным (ОБ), если базисные векторы попарно ортогональны.
Базис называется ортонормированным (ОНБ), если базисные векторы попарно ортогональны и имеют единичную длину.
Т5 (О линейной зависимости 4-х векторов)
Всякие 4 вектора линейно зависимы.
Проекция вектора на ось
О. Ось – прямая, с заданным на ней направлением с помощью единичного вектора  , орта оси. (орт – вектор единичной длины).
, орта оси. (орт – вектор единичной длины).
О. Проекция точки А на ось – основание перпендикуляра, опущенного из этой точки.
О. Вектор - проекция вектора  на ось – вектор
на ось – вектор  , где
, где  - проекции точек
- проекции точек  на ось.
на ось.
О. Скалярная проекция (или просто проекция) вектора  на ось
на ось  - число, определяемое как:
- число, определяемое как: 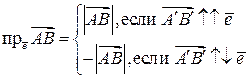
Свойства проекции:
1) 
2) 
О. Угол между векторами  - наименьший угол между этими векторами, отложенными из одной точки. Векторы
- наименьший угол между этими векторами, отложенными из одной точки. Векторы  называются ортогональными (
называются ортогональными ( ), если угол между ними равен π/2.
), если угол между ними равен π/2.
Т. (О вычислении проекции)
Пусть  - угол между векторами
- угол между векторами  . Тогда
. Тогда 
 Скалярное произведение
Скалярное произведение
О. Скалярное произведение векторов  - число
- число  , определяемое как:
, определяемое как:
 где
где  - угол между векторами.
- угол между векторами.
Из определения следует:
1)  (связь проекции и скалярного произведения)
(связь проекции и скалярного произведения)
2) 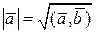 (выражение длины вектора через скалярное произведение)
(выражение длины вектора через скалярное произведение)
3)  (выражение угла между векторами через скалярное произведение)
(выражение угла между векторами через скалярное произведение)
Свойства скалярного произведения.
1)  - коммутативность
- коммутативность
2)  - линейность
- линейность
3)  - неравенство Коши-Буняковского
- неравенство Коши-Буняковского
4)  - неравенство треугольника
- неравенство треугольника
5)  - критерий ортогональности
- критерий ортогональности
Пусть  - ОНБ и
- ОНБ и  ,
,  . Тогда
. Тогда 
Векторное произведение
О. Упорядоченная тройка некомпланарных векторов  называется правой (левой), если с конца вектора
называется правой (левой), если с конца вектора 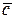 кратчайший поворот от
кратчайший поворот от  к
к  виден против (по) часовой стрелке.
виден против (по) часовой стрелке.
Свойства ориентации тройки векторов:
1) Ориентация тройки векторов не меняется при циклической перестановке.
2) Ориентация тройки меняется при перестановке двух векторов местами.
О. Векторное произведение векторов  - вектор
- вектор  . Удовлетворяющий условиям:
. Удовлетворяющий условиям:
1) 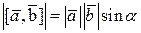 , где
, где  - угол между
- угол между 
2) 
3) 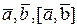 - правая тройка.
- правая тройка.
Свойства векторного произведения:
1)  - антикоммутативность
- антикоммутативность
2)  - линейность
- линейность
3)  , где
, где  - площадь параллелограмма, построенного на векторах
- площадь параллелограмма, построенного на векторах  , как на сторонах.
, как на сторонах.
4)  - критерий коллинеарности векторов
- критерий коллинеарности векторов  .
.
Пусть  - ОНБ и
- ОНБ и  ,
,  . Тогда
. Тогда 
Смешанное произведение
О. Смешанное произведение 3 –х векторов  - число, определяемое как:
- число, определяемое как:  .
.
Т1.(О геометрическом смысле смешанного произведения)
Пусть векторы  некомпланарны и
некомпланарны и  - параллелипипед, построенный на векторах
- параллелипипед, построенный на векторах  как на сторонах. Тогда:
как на сторонах. Тогда:

Следствия:
1. 
2.  =
= 
Т.2 (Критерий компланарности)
 - компланарны
- компланарны 
Пусть  - базис и
- базис и  ,
,  ,
,
 . Тогда
. Тогда 