Постановка задачи
Найти решение системы линейных уравнений заданной в матричном виде с параметрами.
А=  Х=
Х= 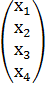 В=
В= 
Теоретическое обоснование
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
 a11х1+а12х2+…+а1nхn=b1
а21х1+а22х2+…+а2nхn=b2
...
as1х1+аs2х2+…+аsnхn=bs (1) a11х1+а12х2+…+а1nхn=b1
а21х1+а22х2+…+а2nхn=b2
...
as1х1+аs2х2+…+аsnхn=bs (1)
|
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких, что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет, хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
 Совместная система вида (1) может иметь одно или более решений: если r=n, то система имеет единственное решение; если r<n и хотя бы одно из чисел dr+1,...,dnотлично от нуля, то система несовместна; если r<n и dr+1=...=dn=0, то систему можно записать в виде:
Совместная система вида (1) может иметь одно или более решений: если r=n, то система имеет единственное решение; если r<n и хотя бы одно из чисел dr+1,...,dnотлично от нуля, то система несовместна; если r<n и dr+1=...=dn=0, то систему можно записать в виде:
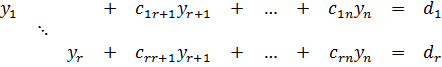
и для любого набора αr+1,...,αnэлементов поля Р существует единственное решение системы, удовлетворяющее условиям yr+1=αr+1,...,yn=αn.
Определение. Упорядоченная линейно независимая подсистема В системы векторов Т арифметического пространства называется базисом системы Т, если любой вектор системы Т является линейной комбинацией векторов подсистемы В.
Определение. Рангом системы векторов называется число элементов в любом базисе этой системы.
Теорема (Кронекера-Капелли).
Система линейных уравнений
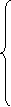 a11х1+а12х2+…+а1nхn=b1
a11х1+а12х2+…+а1nхn=b1
а21х1+а22х2+…+а2nхn=b2
...
as1х1+аs2х2+…+аsnхn=bs
совместна тогда и только тогда, когда

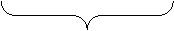 rank
rank  =rank
=rank 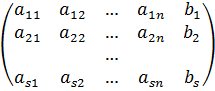 .
.
А А1
Доказательство. 1. Пусть система совместна и (α1,α2,…,αn) – её решение.
 Тогда имеем систему тождеств:
Тогда имеем систему тождеств:
а11α1+а12α 2+…+а1nαn=b1
а21α 1+а22α 2+…+а2nαn=b2
...
as1α 1+ аs2α 2+…+ аsnα n=bs
которую можно записать в виде тождества между вектор-столбцами:
α1 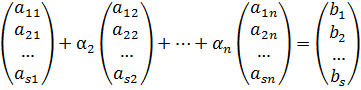 .
.
Последнее тождество означает, что столбец свободных членов системы уравнений является линейной комбинацией столбцов матрицы коэффициентов этой системы. Следовательно, система вектор – столбцов матрицы А эквивалентна системе вектор – столбцов матрицы А1. Эквивалентные системы векторов имеют одинаковые ранги, и поэтому ранги упомянутых в условии матриц равны.
2. Пусть ранги упомянутых в условии матриц А и А1 равны r и пусть 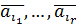 - базис системы столбцов матрицы А. В силу равенства рангов, этот базис является также базисом системы столбцов матрицы А1. Следовательно, столбец
- базис системы столбцов матрицы А. В силу равенства рангов, этот базис является также базисом системы столбцов матрицы А1. Следовательно, столбец 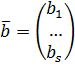 является линейной комбинацией столбцов
является линейной комбинацией столбцов 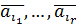 , т.е. существуют такие
, т.е. существуют такие  из поля Р, что имеет место тождество:
из поля Р, что имеет место тождество: 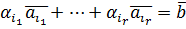 .
.
Последнее тождество, очевидно, не изменится, если в его левую часть мы вставим в качестве слагаемых те вектор – столбцы А, которые не вошли в базис 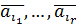 , умноженные на коэффициент 0. После такой вставки мы получим тождество:
, умноженные на коэффициент 0. После такой вставки мы получим тождество: 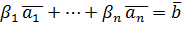 , в котором βj=αj, если
, в котором βj=αj, если
j  , и βj=0, если j
, и βj=0, если j  . Теперь ясно, что
. Теперь ясно, что 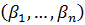 - решение исходной системы линейных уравнений.
- решение исходной системы линейных уравнений.
Методы решения линейных уравнений:
§ Метод Гаусса
§ Метод Гаусса — Жордана
§ Метод Крамера
§ Матричный метод
Пример
Рассмотрим решение конкретной системы линейных уравнений заданной в матричном виде с параметрами:
А=  Х=
Х= 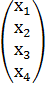 В=
В= 
Решение:
Рассмотрим минор 4-го порядка расширенной матрицы и посчитаем определитель.
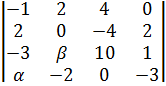 Умножим вторую строку и третий столбец на ½ и получим.
Умножим вторую строку и третий столбец на ½ и получим.
4  Прибавим вторую строку к первой и три вторых строки к третьей строке.
Прибавим вторую строку к первой и три вторых строки к третьей строке.
4 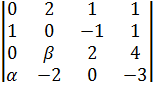 Произведем разложение по первому столбцу.
Произведем разложение по первому столбцу.
4*(-α* 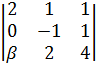 -1*
-1*  )=4*(-α*(2*
)=4*(-α*(2* 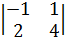 +β*
+β* 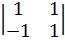 )-1*(-1*
)-1*(-1* 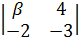 +2*
+2* 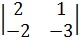 ))=4*(-α*(-12+2*β)-1*((3*β-8)-8))=4*(12*α-2*β*α-3*β+16)
))=4*(-α*(-12+2*β)-1*((3*β-8)-8))=4*(12*α-2*β*α-3*β+16)
4*(12*α-2*β*α-3*β+16)=0
12*α-2*β*α-3*β+16=0
16-3*β- α*(2*β-12)=0
16-3*β= α*(2*β-12) Выразим α.
α= 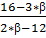
При α≠ 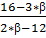 система несовместна т.к. r(A)≤3, a r(AB)=4 и при β≠6 т. к. 2*β-12≠0
система несовместна т.к. r(A)≤3, a r(AB)=4 и при β≠6 т. к. 2*β-12≠0
Рассмотрим минор третьего порядка матрицы А с параметром β:
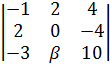 Прибавим ½ второй строки к первой строке.
Прибавим ½ второй строки к первой строке.
 Вычтем второй столбец из третьего.
Вычтем второй столбец из третьего.
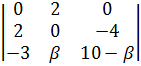 Разложим по первой строке.
Разложим по первой строке.
-2  =-2*(20-2*β-12)=-2(8-2*β)
=-2*(20-2*β-12)=-2(8-2*β)
2(8-2*β)=0; 8-2*β=0; При β≠4 r(A)=3
При β=4 α= 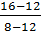 =-1;
=-1;
При α=-1
 умножим на ½ вторую строку, второй и третий столбец.
умножим на ½ вторую строку, второй и третий столбец.
8 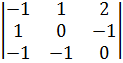 Прибавим вторую строку к первой.
Прибавим вторую строку к первой.
8 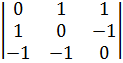 Разложим по первой строке.
Разложим по первой строке.
8*(-1* 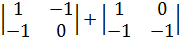 )=8*(1-1)=8*0=0
)=8*(1-1)=8*0=0
При α=-1 и β=4 r(A)=2, a r(AB)=3; r(A)≠r(AB) Система не совместна при α=-1 и β=4.
При β≠4 и при β≠6 r(A)=3, a r(AB)=3 т.к. r=3=n система совместна и имеет одно решение.
 Умножим на ½ вторую строку.
Умножим на ½ вторую строку.
 Прибавим к первой строке две вторых.
Прибавим к первой строке две вторых.
 Прибавим к третьей строке три вторых строки.
Прибавим к третьей строке три вторых строки.
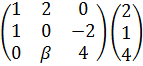 Вычтем из второй строки первую.
Вычтем из второй строки первую.
 Прибавим к третьей строке две вторых.
Прибавим к третьей строке две вторых.
 Выразим
Выразим 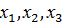 .
.
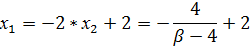
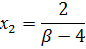
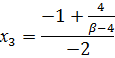
Проверка
β=2 и α= 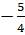
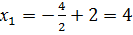 ;
;  ;
; 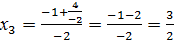 ;
;
-1*4+2*(-1)+4*  =0
=0
2*4-4*  =2
=2
-3*4+2*(-1)+10*  =1
=1
-  *4+2=-3
*4+2=-3
Вывод.
При β≠4 и при β≠6 r(A)=3, a r(AB)=3 т.к. r=3=n система совместна и имеет одно решение.
Список использованной литературы
1. Курош А.Г. Курс высшей алгебры. – М.: Государственное издательство технико-теоретической литературы, 1956. – С.380
2. Некрасов К.Г. Системы линейных уравнений. Методическая разработка для студентов первого курса математических специальностей. – Тверь.: Отпечатано на математическом факультете ТвГУ, 2011. – С.16
3. Некрасов К.Г.Арифметические пространства. Ранг матрицы. Методическая разработка для студентов математического факультета. – Тверь.: Отпечатано кафедрой алгебры и математической логики ТвГУ, 2009. – С.20