До сих пор линия рассматривалась в установившемся гармоническом режиме. Очевидно, перед тем, как этот режим установился, должны были произойти переходные процессы. Напомним, что переходной процесс возникает за счет скачкообразного изменения каких-либо из параметров – коммутаций.
Определим общий подход к решению такого типа задач.
Запишем телеграфные уравнения:
Применим к этим уравнениям преобразование Лапласа по времени t, считая 
параметром. Тогда функциям времени будут соответствовать изображения:
.
С учетом свойств преобразования Лапласа телеграфные уравнения в операторном виде примут вид:
(1).
В дальнейшем будем рассматривать переходные процессы в линии без начальных условий. При этом уравнения (1) упростятся:
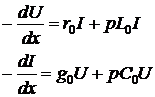(2)
Аналогичные по структуре уравнения были исследованы для комплексных амплитуд. Поэтому на основании ранее сделанных выкладок, получаем разные формы уравнений передачи линии в операторном виде:
(3),
где 
.
Далее будет показано, что первое слагаемые в каждом из этих уравнениях – это операторное изображение падающей волны, а второе – отраженной. Если 
, то отраженной волны не будет. Приведенные выше уравнения дают лишь стратегию поиска и должны рассматриваться для конкретного режима работы и конкретного вида воздействия. Рассмотрим некоторые из них.
1. Линия без потерь, согласованная во всем диапазоне частот.
В данном случае 
, а сопротивление нагрузки и волновое сопротивление равны: 
. Из уравнений (3) с учетом того, что 
следует – слагаемые, соответствующее отраженной волне превращаются в ноль. То есть, отраженной волны нет, а есть только падающая волна: 
(для тока аналогично). Поскольку отраженной волны нет, то 
и выражение для падающей волны принимает вид: 
, где 
.
Как видим, волновое сопротивление не зависит от переменной 
, а 
зависит прямопропорционально. Подставим значения и 
в выражение для падающей волны: 
. Известно, что 
, где 
- фазовая скорость. Перепишем выражение для падающей волны: 
(вспомните теорему о временном сдвиге оригинала!). Получаем, что в зависимости от координаты падающая волна с разной задержкой распространяется по всей линии.
 |
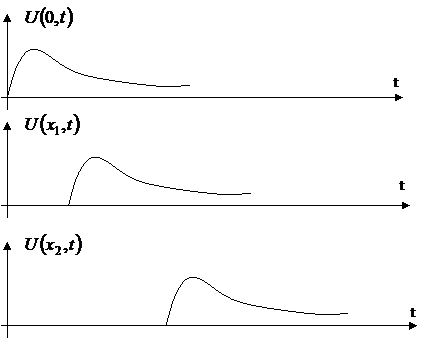Если зафиксировать время и изменять координату , то графики примут вид:
 |
2. В линии есть потери.Линия согласована.
Если в линии есть потери, также возможен случай, когда сигнал будет передаваться без искажений. Для этого должно выполняться условие: 
. Проверим это. С учетом приведенного условия постоянная распространения примет вид:
Как видим, данная линия длиной 
эквивалентна четырехполюснику, который пропускает сигнал без искажений, но с задержкой.
 | |||||
| |||||
 |
Такая линия может быть заменена четырехполюсником с коэффициентом передачи, равным: 
.
3. Случай многократных отражений.
Если сопротивление нагрузки не равно волновому сопротивлению, то появится отраженная волна. Найдем коэффициенты отражения по напряжению в конце и начале линии:
. Время пробега волны по линии от генератора к нагрузке - 
.
Рассмотрим распределение напряжения вдоль линии в разные моменты времени после включения:
|
( –длина линии, v – скорость).
Пока отраженной волны нет: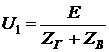 
, т.к. 
. При отсутствии отраженной волны напряжение в линии распределено по закону: 
.
2. 
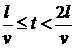
Так как Zн≠Zв , то появится отраженная от нагрузки волна Uо1. U01 перемещается к генератору, поэтому напряжение в линии будет состоять из двух слагаемых:
.
В итоге получаем распределение напряжения для случая, когда в линии, кроме падающей волны, существует волна, отразившаяся от нагрузки первый раз.
.
3. 
Если сопротивление генератора не равно волновому (то есть n1≠0), то волна, отразившаяся от нагрузки, придя к генератору, отразится от него и направится в сторону нагрузки. Обозначим ее U02.
Выражение для напряжения в линии, в которой существует падающая и двукратно отразившаяся волна примет вид: 
4. 
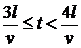
Проводя аналогичные рассуждения, для данного интервала времени можно записать:
