МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Цель работы. Практическое усвоение формул обработки равноточных измерений одной величины, усвоение методов определения наиболее точного и достоверного значения измеренной величины, методов доверительного оценивания.
Состав задачи. В результате повторных равноточных измерений величины Х получен ряд результатов:
х1, х2,............хn,
с одинаковыми средними квадратическими ошибками:
m1 = m2 =.......= mn = m.
Исходные данные: Вариант получают моделированием в программе MATRIX.exe., преподаватель задает доверительную вероятность β.
Задание: По результатам измерений надо вычислить:
- наиболее достоверное значение измеренной величины;
- определить средние квадратические ошибки (далее ско) одного измерения и среднего арифметического,
- определить необходимую точность их определения.
-выполнить доверительное оценивание при заданной доверительной вероятности β:
а) математического ожидания измеренной величины,
б) среднего квадратического отклонения одного измерения;
в) среднего квадратического отклонения среднего арифметического при.
Порядок выполнения задания.
1. Определяется наиболее достоверное значение из ряда равноточных измерений. Это среднее арифметическое, которое вычисляется по формуле
, (1.1)
где 
– сумма измеренных значений, 
- число измерений.
Вместо формулы (1.1) используют более удобную формулу
. (1.2)
Для этого из приведенного ряда измерений выбирают условное (обычно кратное десяти наименьшее) значение x0 и вычисляют величину εі по формуле
, (1.3)
где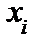 
– измеренное значение.
Чтобы не накапливать ошибки округления, среднее 
вычисляют с числом десятичных знаков хотя бы на один больше, чем в измеренных значениях .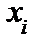
2.Вычисляют отклонение результатов измерений 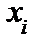от среднего значения
(1.4)
и выполняют 1 контроль
(1.5)
где 
предельная ошибка округления, равная 0,5 единицы последнего удерживаемого знака.
3.Вычисляют 
с контролем (2 контроль)
(1.6)
4. Определяют средние квадратические ошибки:
а) среднюю квадратическую ошибку отдельного измерения по формуле Бесселя
; (1.7)
б) среднюю квадратическую ошибку среднего арифметического
; (1.8)
5. Для определения необходимой точности вычисления ско получают среднюю квадратическую ошибку средней квадратичной ошибки
; (1.9)
и среднюю квадратическую ошибку средней квадратичной ошибки среднего арифметического
. (1.10)
Делают вывод о необходимой точности вычисления ско.
6.Определяют доверительные интервалы для:
а) математического ожидания измерения
(1.11)
где параметр tβ выбирают из таблиц распределения Сьюдента (например, приложение V в [ 1 ] или приложения (2)) по заданной доверительной вероятности β и числу степеней свободы k = n – 1;
б) среднего квадратического отклонения отдельного измерения
(1.12)
в) среднего квадратического отклонения среднего арифметического
(1.13)
где m и М средние квадратические ошибки, вычисленные по формулам (1.7) и (1.8). Коэффициенты 
и 
выбирают из таблиц (приложение VIII в [ l ] или приложение (3)) по числу степеней свободы 
и по выбранной доверительной вероятности β.
Пример. Для исследования нового теодолита выполнено измерение угла 12 раз. По результатам измерений выполнить обработку ряда равноточных измерений. Доверительные оценки получить с вероятностью 0,95.
Вычисления выполним в таблице 1.1.
Таблица 1.1
| № измерения. | Измеренный угол α | ε, сек. | v, сек. | ε2,сек.2 | v2, сек.2 | Контрольные вычисления |
| 154039'34,3» | 4,3 | -0,64 | 18,49 | 0,4096 | ||
| 154039'33,6» | 3,6 | -1,34 | 12,96 | 1,7956 | 1 контроль | |
| 154039'37,7» | 7,7 | 2,76 | 59,29 | 7,6176 | 0,02 ≤ 0,06 | |
| 154039'33,2» | 3,2 | -1,74 | 10,24 | 3,0276 | 2 контроль | |
| 154039'33,4» | 3,4 | -1,54 | 11,56 | 2,3716 | 23,509 = 23,509 | |
| 154039'34,3» | 4,3 | -0,64 | 18,49 | 0,4096 | ||
| 154039'35,3» | 5,3 | 0,36 | 28,09 | 0,1296 | ||
| 154039'34,5 | 4,5 | -0,44 | 20,25 | 0,1936 | ||
| 154039'36,3» | 6,3 | 1,36 | 39,69 | 1,8496 | ||
| 154039'34,6» | 4,6 | -0,34 | 21,16 | 0,1156 | ||
| 154039'37,3» | 7,3 | 2,36 | 53,29 | 5,5696 | ||
| 154039'34,8» | 4,8 | -0,14 | 23,04 | 0,0196 | ||
| Σ | 59,3 | 0,02 | 316,55 | 23,509 |
Выбираем наименьшее значение х0 = 154039'30'',0
По формулам (1.2 – 1.10) вычисляем:
среднее арифметическое
среднюю квадратическую ошибку отдельного измерения по формуле Бесселя
,
среднюю квадратическую ошибку среднего арифметического
Определить необходимую точность определения ско для чего вычисляем среднюю квадратическую ошибку средней квадратической ошибки
и среднюю квадратическую ошибку средней квадратической ошибки среднего арифметического
Сравним значения средних квадратических ошибок 
и 
, и их средних квадратических ошибок 
и 
. Из сравнения видно, что при вычислении средних квадратических ошибок достаточно оставлять две значащие цифры, при этом вторая цифра уже неточная.
Строим доверительные интервалы:
а) доверительный интервал для математического ожидания измеренной величины:
значение tβ найдем по доверительной вероятности β = 0,95 и по числу степеней свободы k = 12―1 = 11, из таблиц распределения Сьюдента в приложении (2) tβ = 2,2.
154039'34,''942 – 2,2*0,''42 
154039'34,''942 + 2,2*0,''42 или
154039'34,''02 154039'35'',87;
б) доверительный интервал для среднего квадратического отклонения отдельного измерения:
значение и найдем по доверительной вероятности 
и по числу степеней свободы 
из таблиц приложения (3). Значения = 0,708 и 
=1,698.
1″,5 * 0,708 ≤ 
≤ 1″,5 * 1,698
или
1″,06 ≤ ≤ 2'',55 ″,
в) доверительный интервал для среднего квадратического отклонения среднего арифметического:
0″,42 *0,708 
0″,42*1,698
или
0″,30 
0″,71
Вывод: