Филиал ГОУ ВПО УГНТУ в г. Салавате
Кафедра химико-технологических процессов
РАСЧЁТ КРИТИЧЕСКИХ, ТЕПЛОФИЗИЧЕСКИХ
СВОЙСТВ И МОЛЕКУЛЯРНОЙ МАССЫВЕЩЕСТВ
Учебно-методическое пособие
Уфа 2007
Учебно-методическое пособие предназначено для студентов высших учебных заведений инженерных специальностей, изучающих курс «Инженерные расчёты физико-химических свойств веществ».
В пособии представлены некоторые методы расчёта критических, теплофизических свойств и молекулярной массы веществ, а также примеры расчёта.
Рекомендуется для практических занятий и выполнения расчётно-графических работ.
Составители: Сидрачёва И.И., ассистент
Будник В.А., ассистент
Введение
В ходе технологических расчётов процессов и аппаратов нефтепереработки требуется знание физико-химических свойств химических веществ и нефтяных фракций.
В справочной литературе обычно приводятся данные по физико-химическим свойствам веществ для ограниченного количества наиболее распространённых соединений. В связи с этим возникает проблема аналитического расчёта численных значений физико-химических свойств веществ и учёта влияния параметров процесса на свойства веществ.
В данном учебно-методическом пособии приведён ряд методов расчёта основных физико-химических свойств химических соединений и нефтяных фракций. С его помощью студенты могут освоить методологию расчёта, сопоставить различные методы по точности определения свойств веществ.
1 РАСЧЁТ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВ
Значительная часть инженерных методов расчёта физико-химических свойств веществ базируется не на фактических значениях параметров, а на их приведённых величинах. Под приведёнными параметрами понимают отношение фактической величины параметра к его критическому значению. Например, приведённая температура:
,
где 
критическая температура для данного вещества.
В связи с этим достаточно достоверное определение критических параметров веществ необходимо для дальнейшего правильного расчёта физико-химических свойств веществ.
Состояние вещества, при котором исчезает различие между его жидкой и газообразной фазами, называется критическим.
Критическая температура – максимальная температура, при которой ещё могут сосуществовать в равновесии паровая и жидкая фазы. При температурах выше критической конденсация паров данного вещества невозможна. В критической точке фиксируются значения критического давления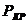 
и критического удельного объёма 
.
Критические параметры вещества связаны соотношением
где 
– критический коэффициент сжимаемости;
универсальная газовая постоянная.
По опытным данным, критический коэффициент сжимаемости изменяется в пределах 0,26 – 0,29 (для большинства органических соединений), хотя имеются исключения.
Критические температура, давление, объем представляют собой три широко используемые константы чистых веществ. Тем не менее, современные измерения их почти не производятся.
Рассмотрим расчетные методы определения критических свойств чистых компонентов.
1.1 РАСЧЕТ КРИТИЧЕСКОЙ ТЕМПЕРАТУРЫ
Критической температурой чистого вещества называется максимальная температура, при которой жидкая и паровая фазы могут существовать в равновесии.
Критическую температуру жидкости Ткр (К) можно приближенно определить, зная температуру кипения жидкостей Тк (К) при атмосферном давлении.
1.1. Правило Гульдберга:
(1.1)
1.2. Модифицированное правило Гульдберга:
(1.2)
1.3. Метод Мейсснера – Реддинга: для соединений с Тк<235 К и простых веществ:
(1.3)
Для соединений с Тк , лежащей в пределах 235 – 600 К, можно пользоваться уравнениями:
1.3.1. Для алканов и алкенов:
(1.4)
1.3.2. Для ароматических углеводородов и нафтенов без галогенов и серы:
, (1.5)
где 
соотношение числа атомов углерода, находящихся вне кольца, к общему числу атомов углерода в соединении.
1.3.3. Для соединений, содержащих атомы галогенов и серы:
, (1.6)
где 
число атомов галогена или серы в молекуле.
1.4. Для углеводородов можно использовать уравнение Гетеса и Тодоса:
(1.7)
1.5. Для н-алкановых углеводородов критическая температура рассчитывается по уравнению Тиличеева и Татевского:
(1.8)
где 
число атомов углерода.
1.6. Можно использовать уравнения Мамедова:
1.6.1. Для н-алкановых углеводородов:
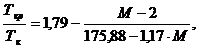(1.9)
где 
молекулярная масса углеводорода.
1.6.2. Для ароматических углеводородов – гомологов бензола:
(1.10)
где 
средняя мольная температура кипения жидкой фракции при перегонке;
плотность жидкого углеводорода при 288 К.
1.7. Критическая температура нормальных парафиновых углеводородов определяется по уравнению
(1.11)
1.8. Критическая температура может быть определена по формуле Нокая
(1.12)
где плотность жидкости, кг/м3.
1.9. Метод Лидерсена:
(1.13)
где
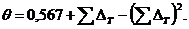(1.14)
Величины 
берутся по таблице 1.1.
1.10. Критическую температуру углеводородов и нефтяных фракций вычисляют также по уравнению Итона и Портера:
(1.15)
где
(1.16)
где Т50% - температура выкипания 50% фракции по ASTM.
Таблица 1.1 – Составляющие для определения критических параметров
(по Лидерсону)
| Атом, группа, связь |
| 
| 
|
| -СН3 и -СН2- | 0,020 | 0,725 | |
| -СН2- (в кольце) | 0,013 | 0,588 | 44,5 |
| ׀ -СН ׀ | 0,012 | 0,671 | |
| ׀ -СН (в кольце) ׀ | 0,012 | 0,613 | |
| ׀ -С- ׀ | 0,000 | 0,671 | |
| ׀ - С -(в кольце) ׀ | (- 0,007) | (0,492) | (31) |
| ׀ =СН2 и =СН | 0,018 | 0,632 | |
| ׀ =С- | 0,000 | 0,632 | |
| ׀ =СН (в кольце) | 0,011 | 0,492 | |
| ׀ =С-(в кольце) | 0,011 | 0,492 | |
| =С= | 0,000 | 0,632 | |
| =С= (в кольце) | 0,011 | 0,492 | |
| =СН и =С- | 0,005 | 0,489 | (36) |
| -F | 0,018 | 0,750 | |
| -CL | 0,017 | 1,020 | |
| -Br | 0,010 | (0,160) | (70) |
| -I | 0,012 | (2,650) | (95) |
| -ОН (спирты) | 0,082 | 0,192 | (18) |
| -ОН (фенолы) | 0,031 | (-0,06) | (3) |
| -О- | 0,021 | 0,511 | |
| -О- (в кольце) | (0,014) | (0,383) | (8) |
| ׀ -С=О | 0,040 | 0,926 |
Продолжение таблицы 1.1
| ׀ - С=О (в кольце) | (0,033) | (0,639) | (50) |
| ׀ НС=О (в альдегидах) | 0,048 | 1,053 | |
| -СООН (кислоты) | 0,085 | (1,277) | |
| -СОО- (сложные эфиры) | 0,047 | 1,501 | |
| =О | (0,02) | (0,383) | (11) |
| -NН2 | 0,031 | 0,303 | |
| ׀ -NН | 0,031 | 0,431 | (37) |
| ׀ -NН (в кольце) | (0,024) | (0,287) | (27) |
| ׀ -N- | 0,014 | 0,543 | (42) |
| ׀ -N- (в кольце) | (0,007) | (0,415) | (32) |
| -СN | (0,060) | (1,149) | (80) |
| -NО2 | (0,055) | (1,341) | (78) |
| -SН и S- | 0,015 | 0,862 | |
| - S- (в кольце) | (0,008) | (0,766) | (45) |
| = S | (0,003) | (0,766) | (47) |
Примечание. В скобках приведены ненадежные данные.
1.11. По уравнению Максвелла:
(1.17)
где 
и 
– эмпирические коэффициенты.
1.12. Критическую температуру жидкостей можно определить по зависимости
, (1.18)
где 
– плотности жидкости при температурах Т1 и Т2, г/см3.
Область применения уравнения (1.18) ограничена условиями:
;
Причем, чем меньше температурный интервал Т, тем отклонение от экспериментальных данных больше.
1.13. Метод Филиппова:
(1.19)
где 
– критическая плотность, г/см3.
(1.20)
где 
плотность при температуре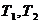 
, г/см3.
1.2 РАСЧЕТ КРИТИЧЕСКОГО ДАВЛЕНИЯ
Критическим называется давление, при котором вещество еще может находиться в жидком состоянии при критической температуре, т.е. это давление насыщенного пара при критической температуре.
1.2.1.Критическое давление жидкостей можно вычислить по формуле Риделя:
(1.21)
где Ркр – критическое давление, Па.
Составляющие для определения а берутся по таблице 1.2. Эти составляющие суммируют с постоянной А=105,4∙10-3.
Таблица 1.2 – Составляющие для определения а (по методу Риделя)
| Атом, группа, связь |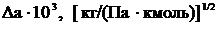 
|
| Постоянная А | 105,4 |
| Н | |
| С | 73,5 |
| F | 73,5 |
| CI | 102,2 |
| Br | 172,5 |
| O | 57,5 |
| N | 44,7 |
| S | 86,2 |
| I | 277,9 |
| Атом кольца | -13,73 |
| С-S | -16 |
| Конденсированные кольца | -31,94 |
| С=С | -19,2 |
| С=О | -38,3 |
| С= N | |
| ОН (спирты) | -35,1 |
| ОН (ароматические спирты) | 67,1 |
| ОН (кислоты) | |
| N - Н | -6,4 |
| С=С | -44,7 |
1.2.2. По формуле Лидерсена – Риделя:
(1.22)
где ΣΔр определяют сложением составляющих, приведенных в таблице 1.1.
2.3. По формуле Бенке:
(1.23)
где 
– число атомов в молекуле.
2.4. Зависимость от парахора Pch и мольной рефракции Rd по Мейсснеру:
(1.24)
Значение Pch и Rd определяют сложением составляющих, приведенных в таблице 1.3 и 1.4.
Таблица 1.3 – Составляющие для определения парахора
| Атом, группа или связь | Составляющая ∙ 103,
|
| СН2 в (СН2)n: n < 12 n > 12 | 7,11 7,17 |
| С | 1,6 |
| Si | 5,51 |
| Н | 2,76 |
| Н (в ОН) | 1,78 |
| Н (в NН3) | 2,22 |
| О | 3,52 |
| О (в эфирах) | 9,75 |
| N | 3,11 |
| P | 7,20 |
| S | 8,73 |
| Si | 11,20 |
| F | 4,64 |
| CL | 9,82 |
| Br | 12,10 |
| I | 16,50 |
| Двойная связь: конец цепи 2-,3- положение 3-,4- положение | 3,40 3,15 2,90 |
| Тройная связь | 8,29 |
| Кольца: трехчленное четырехчленное пятичленное шестичленное | 2,22 1,07 0,53 0,14 |
Таблица 1.4 – Составляющие для определения мольной рефракции
| Атом, связь | Составляющая ∙ 103,
|
| Н | 1,10 |
| С | 2,418 |
| CL | 5,967 |
| Br | 8,865 |
| I | 13,90 |
| O (в гидроксиле) | 1,525 |
| О (в карбониле) | 2,211 |
| О (в простом эфире) | 1,643 |
| СН2 в (СН2)n: | 4,618 |
| СОО | 6,154 |
| Двойная связь | 6,154 |
| Тройная связь | 2,398 |
| Трехчленное кольцо | 0,71 |
| Четырехчленное кольцо | 0,48 |
2.5. Критическое давление как функция критической температуры может рассчитываться по уравнению Льюиса:
(1.25)
где К – константа, берется из таблицы 1.5 или для нефтяных фракций вычисляется по формуле
(1.26)
где Т10%, Т70% - температуры выкипания 10 и 70% фракции, К.
2.6. Критическое давление по формуле Филиппова:
(1.27)
где ρкр – критическая плотность вещества, кг/м3, определяемая как
(1.28)
где ρt, ρ1, ρ2 – плотности вещества при температуре Т, Т1, Т2, г/см3.
Таблица 1.5 – Значения константы К в уравнении Льюиса
| Углеводород или нефтепродукт | К |
| н - парафины (бутан и более тяжелые) | 5,06 |
| изо - парафиновые | 5,1-5,3 |
| нафтеновые | 6,0 |
| ароматические | 6,5-7,0 |
| ароматические без боковых цепей | 6,22 |
| насыщенные циклические углеводороды | 6,05 |
| нефтепродукты прямой перегонки | 6,3-6,4 |
| крекинг – керосин | 6,8-7,0 |
Или критическая мольная плотность вещества рассчитывается по формуле
(1.29)
где R – универсальная газовая постоянная, равная 8,314∙103Дж/(кмоль∙К).
1.3 РАСЧЕТ КРИТИЧЕСКОГО ОБЪЕМА
Объем, который занимает вещество при критических давлении и температуре, называется критическим.
Критический объем не поддается точному определению по той причине, что в критической точке ничтожно малые изменения давления влекут за собой большие изменения объема.
3.1. Критический объем по методу Лидерсона определяется по формуле
(1.30)
где Vкр – критический объем, м3/кмоль.
Величины ΔV берутся по таблице 1.1.
3.2. Метод Ветере, аналогичный методу Лидерсона:
(1.31)
где значения ΔVi для многих групп приведены в таблице 1.6,
Мi – молекулярная масса группы,
Vкр – критический объем, см3/моль.
3.3. Критический объем можно определить исходя из критического коэффициента сжимаемости Zкр:
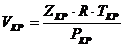, (1.32)
где
. (1.33)
Величины Δz находят по таблице 1.7.
3.4. Критический объем вещества как функция парахора может рассчитываться по следующей формуле:
(1.34)
3.5. По Мейсснеру:
(1.35)
3.6. Формула Тодоса используется для определения Vкр алифатических насыщенных и ненасыщенных углеводородов:
(1.36)
где в – постоянная Ван – дер – Ваальса, определяемая по уравнению
(1.37)
где В – зависит от числа атомов углерода (Nc) и их расположения в молекуле:
для нормальных насыщенных алифатических углеводородов:
В=0,7849 – 0,01337·Nc; (1.38)
для тех же углеводородов, но с разветвленными цепями:
В=0,8100 – 0,0138·Nc; (1.39)
для ненасыщенных алифатических углеводородов:
(1.40)
Таблица 1.6 – Групповые составляющие для определения критического объема по методу Ветере
| Группа | 
| Группа |
|
| Ациклические (вне кольца) | ׀ -С=О (в кольце) | 1,500 | |
| В основной цепи: | |||
| СН3, СН2, СН, С | 3,360 | ׀ НС=О (альдегиды) | 2,333 |
| В боковой цепи: | |||
| СН3, СН2, СН, С | 2,888 | ׀ -NH (вне кольца) | 2,333 |
| =С= | 2,908 | ׀ -NH (в кольце) | 1,736 |
| 2,648 | ׀ -N- (вне кольца) | 1,793 |
| Циклические (в кольце) | |||
| СН2, СН, С | 2,813 | ׀ -N- (в кольце) | 1,883 |
| ׀ ׀ =СН, = - С | 2,538 | -CN | 2,784 |
| F | 0,770 | -NO2 | 1,559 |
| CL | 1,237 | -SH | 1,537 |
| Br | 0,899 | -S- (вне кольца) | 0,591 |
| I | 0,702 | -S- (в кольце) | 0,911 |
| -ОН (спирты) | 0,704 | -СООН | 1,652 |
| -ОН (фенолы) | 1,553 | ׀ -С=О (вне кольца) | 1,765 |
| -О-(вне кольца) | 1,075 | ||
| -О- (в кольце) | 0,790 | ||
| -О-(эпоксиды) | 0,252 |
Таблица 1.7 – Составляющие Z
| Группа или связь | z | Группа или связь | z |
| -Н | 0,0000 | Изомеры | |
| -СН3 или -СН2 | Цис- Транс- | (-0,0022) (-0,0102) | |
| Первые 10 в молекуле | 0,0046 | Связь С=С | (-0,0183) |
| Каждая после десятой | 0,0037 | -NH2: | |
| ׀ ׀ -СН или - С -: ׀ ׀ | алициклическая ароматическая | (0,0097) (0,0252) | |
| Первая в молекуле | -0,0035 | ׀ -NH (алифатическая) | (0,0047) |
| Каждая последующая | 0,0042 | =N- (алифатическая) | - 0,0057 |
| -СН (в кольце) | 0,0025 | -SH | 0,0110 |
| Кольца: | -S- | 0,0082 | |
| трехчленные | (0,0152) | -О- | 0,0076 |
| Пяти и шестичленные | -0,0057 | -О- (в кольце) | 0,0136 |
| Бензольное кольцо | 0,0178 | НСОО- (эфиры муравьиной кислоты): | |
| Положения | При 4 или менее | (0,0360- | |
| Орто- | 0,0122 | атомах С | -0,0040)N |
| Мета- | 0,0072 | -СОО-(сложные эфиры) при < 5 атомах при > 5 атомах | (0,006-0,004)N -0,0075 |
| Пара- | 0,0102 | ||
| Связь С=С: | |||
| первая | 0,0133 | ||
| вторая | (0,0012) | ||
| -F,-CL,-Br,-I (ароматические) | 0,0112 |
1.4 ПРИМЕРЫРАСЧЕТА
Пример 1.4.1. Вычислить критическую температуру этилбутилового эфира по методу Лидерсона, если Тк=365,4 К.
Используя данные таблицы 1.1 приложения находим
По уравнению (1.14):
По уравнению (1.15):
По литературным данным, Ткр = 531 К.
Пример 1.4.2. Вычислить критическую температуру этилбензола по методу Нокая, если Тк=409,3 К, ρ=0,867 г/см3.
По уравнению (1.12):
Ткр= 615,2 К.
По литературным данным, Ткр= 617,1 К.
Пример 1.4.3. Вычислить критическую температуру по методу Мейсснера – Реддинга для изобутилбензола, если Тк = 445,9 К.
По уравнению (1.5):
Ткр=1,41∙445,9 + 66 – 0,4∙(0,383∙445,9 – 93) = 663,6 (К).
По литературным данным, Ткр= 650 К.
Пример 1.4.4. Вычислить Ркр и Vкр трихлорэтана, если Ткр=602 К.
Ркр определяем по формуле Мейсснера. Суммируем составляющие Pch по таблице 2.2 приложения.
(Дж1/4м5/2кмоль-1).
Суммируем составляющие Rd по таблице 2.3 приложения.
(м3/кмоль).
По уравнению (2.4) рассчитываем Ркр:
По литературным данным Ркр= 4,1 МПа.
По методу парахора (3.5) определяем Vкр:
(м3/кмоль).
По литературным данным Vкр = 0,294 м3/кмоль.
Пример 1.4.5. Определить Ткр, Ркр гептана, если М=100 кг/кмоль, при 273 К, ρ0=0,7005 г/см3, а при 293 К ρ=0,6836 г/см3.
По уравнению (1.20) определяем ρкр:
г/см3.
По уравнению (1.19):
К.
По уравнению (2.7) определяем Ркр:
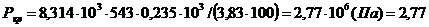МПа.
По литературным данным Ткр = 540,2 К, Ркр = 2,7 МПа.
Пример 1.4.6. Вычислить Vкр этилпропилового эфира; Ткр = 498 К, Ркр=3,23 МПа.
Воспользовавшись уравнением Лидерсона (3.1) и таблицей 1.1 приложения:
м3/кмоль.
м3/кмоль.
С другой стороны, по уравнению (3.4) и таблице 3.2 приложения:
Тогда по уравнению (3.3):
м3/кмоль.
Экспериментальное значение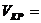 
0,339 м3/кмоль.
2 РАСЧЁТ МОЛЕКУЛЯРНОЙ МАССЫНЕФТЯНЫХ ФРАКЦИЙ
Молекулярная масса является одной из основных физико-химических характеристик нефтей и нефтепродуктов. Её используют для вычисления других физико-химических свойств, при технологических расчётах аппаратуры.
Молекулярная масса индивидуальных веществ легко рассчитывается по их химической формуле и атомным массам элементов, входящих в состав молекул.
Среднюю молекулярную массу смеси можно определить, зная мольную долю и молекулярную массу каждого компонента смеси:
(2.1)
где 
содержание компонентов в смеси, мольные доли;
молекулярные массы компонентов смеси.
Если известны не мольные доли, а массы компонентов смеси, можно пользоваться следующей формулой:
, (2.2)
где 
масса компонентов, кг;
молекулярная масса компонентов.
Применительно к нефтяным системам, представляющим собой многокомпонентные смеси, под молекулярной массой подразумевается средняя молекулярная масса – молекулярная масса гипотетического углеводорода, имеющего усреднённые значения элементного состава, температуры кипения и плотности.
Между молекулярной массой и температурой кипения нефтяных фракций существует определённая зависимость: чем больше молекулярная масса нефтяной фракции, тем выше её температура кипения. Из расчётных методов определения молекулярной массы наибольшее распространение получила формула Б.М. Войнова, уточнённая А.С.Эйгенсоном, основанная на данной зависимости.
(2.3)
где 
средняя молекулярная температура кипения (для узких фракций можно брать среднюю температуру кипения при разгонке по ГОСТ), ˚С;
характеризующий фактор.
Характеризующий фактор определяет химическую природу нефтепродукта. Для парафинистых нефтепродуктов К = 12,5 – 13, для ароматизированных около 10 и менее, для нафтено-ароматических К = 10 – 11. Характеризующий фактор определяют по формуле:
, (2.4)
где 
относительная плотность данной фракции.
Среднюю молекулярную температуру кипения нефтепродукта можно определить по формуле:
, (2.5)
где 
содержание узких фракций, мольные доли;
средние (арифметические) температур начала и конца кипения узких фракций, составляющих данный нефтепродукт, ˚С.
Если известна только плотность нефтепродукта, его молекулярную массу можно определить по формуле Крэга:
. (2.6)
3 РАСЧЁТ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ВЕЩЕСТВ
Основой тепловых технологических расчётов аппаратов нефтеперерабатывающих заводов являются такие теплофизические характеристики веществ как теплоёмкость, теплота парообразования и конденсации, энтальпия (теплосодержание), теплота сгорания и др.
3.1 РАСЧЁТ ТЕПЛОТЫПАРООБРАЗОВАНИЯ
Теплота парообразования или противоположная ей по знаку теплота конденсации есть разность энтальпий насыщенного пара и равновесной ему закипающей жидкости.
На основе уравнений состояния разработан ряд простых, но достаточно точных уравнений для расчёта теплоты парообразования. Например, уравнение Чена
(3.1)
и уравнение Риделя
(3.2)
Пример 3.1.1 Рассчитать теплоту парообразования гексана при нормальной температуре кипения 341,9 К (1 атм) методами Чена и Риделя. Критическая температура гексана равна 507,3 К, критическое давление 29,9 атм. Табличное значение теплоты парообразования гексана равно 6896 кал/моль.
По методу Чена
Погрешность расчёта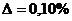 
.
По методу Риделя
Погрешность расчёта 
3.2 РАСЧЁТ ТЕПЛОЁМКОСТИ
Теплоёмкостью называют количество теплоты, которое необходимо сообщить веществу, чтобы повысить температуру какой-либо количественной единицы на 1 ˚С.
В зависимости от выбранной количественной единицы вещества различают мольную теплоёмкость (в кДж/(кмоль·К) или ккал/(кмоль·К), массовую теплоёмкость (в кДж/кг·К или ккал/кг·К) или объёмную теплоёмкость (в кДж/м3·К или ккал/м3·К).
3.2.1 РАСЧЁТ ТЕПЛОЁМКОСТИ ВЕЩЕСТВ В ПАРОВОЙ ФАЗЕ
Для теоретического расчёта теплоёмкости необходимо знание подробных структурных и спектральных данных. Теплоёмкость вещества относится к состоянию идеального газа. Для перехода к реальным газам часто используют термин «нулевое давление», при котором уравнения состояния идеального и реального газов совпадают. Для инженерного расчёта теплоёмкости обычно применяют термическое уравнение в виде разложения зависимости теплоёмкости от температуры в полиноминальный ряд
(3.3)
где 
удельная теплоёмкость при «нулевом давлении», кал/(моль·град);
Т – температура. К;
константы.
При использовании принципа аддитивности константы 
уравнения (3.3) выражают в форме суммы групповых составляющих, характеризующих вклады различных структурных элементов молекулы в соответствующий коэффициент, тогда уравнение (3.3) приобретает вид:
, (3.4)
где 
число структурных элементов 
типа с вкладами 
для соответствующих коэффициентов .
Наиболее часто используют составляющие коэффициентов , рассчитанные Джонсоном и Хуангом (таблица 3.1).
Пример 3.2.1. Рассчитать теплоёмкость паров этилбензола в состоянии идеального газа при 500 К, используя групповые составляющие Джонсона и Хуанга. Опытное значение теплоёмкости при 500 К 49,35 кал/(моль·К).
Таблица 3.1 – Составляющие для расчёта теплоёмкости паров по методу Джонсона и Хуанга
| Группа |  
| 
| 
| 
|
| -СН3 | 0,427 | 2,183 | -0,0863 | 0,00111 |
| -СН2- | -0,186 | 2,243 | -0,1263 | 0,00274 |
| =СН2 | 0,662 | 1,770 | -0,0874 | 0,00167 |
| =СН- | -0,239 | 1,663 | -0,1056 | 0,00260 |
| -7,576 | 11,007 | -0,729 | 0,01801 |
 СН
| 2,017 | 1,400 | -0,1157 | 0,00352 |
| – С
| -5,252 | 3,887 | -0,4400 | 0,01521 |
| -СН2- (5-членное кольцо) | -2,137 | 2,473 | -0,1195 | 0,00198 |
| -СН2- (6-членное кольцо) | -2,318 | 2,471 | -0,1294 | 0,00257 |
| ׀ -СН ׀ | -1,942 | 2,832 | -0,2281 | 0,00661 |
| ׀ -С- ׀ | -4,655 | 3,682 | -0,3551 | 0,00982 |
| ׀ С = ׀ | -0,0535 | 1,342 | -0,1019 | 0,00273 |
Составим таблицу групповых составляющих для этилбензола, имеющего структуру
| Группа |
|
|
|
|
| 1 группа -СН3 | 0,427 | 2,183 | -0,0863 | 0,00111 |
| 1 группа -СН2- | -0,186 | 2,243 | -0,1263 | 0,00274 |
| 5 групп =СН- | 5(-0,239) | 5(1,663) | 5(-0,1056) | 5(0,00260) |
| ׀ 1 группа С = ׀ | -0,0535 | 1,342 | -0,1019 | 0,00273 |
| Всего: | -1,0075 | 14,083 | -0,8425 | 0,01958 |
Таким образом, при 500 К
кал/(моль·К)
Погрешность расчёта 
1,46%.
Имеется большое число эмпирических уравнений для расчёта теплоёмкости веществ в паровой фазе. Например, для нормальных условий (в Дж/(моль·К))
(3.5)
а для повышенных температур
(3.6)
(3.7)
где 
число атомов углерода и водорода в молекуле.
3.2.2 расчёт теплоёмкости веществ в жидкой фазе
Большинство органических жидкостей имеют теплоёмкость в пределах 0,4 – 0,5 кал/(г·К), величина теплоёмкости несколько увеличивается с ростом температуры. Влияние давления на теплоёмкость жидкости, за исключением критической области, также невелико и для большинства низкокипящих жидкостей величина теплоёмкости уменьшается примерно на 10% при увеличении давления на 2500 атм.
Достаточно простым является аддитивно-групповой метод расчёта теплоёмкости, разработанный Джонсоном и Хуангом, в котором соответствующие групповые составляющие молекулы (таблица 3.2) просто суммируются.
Таблица 3.2 – Атомно-групповые составляющие для расчёта теплоёмкости жидкостей при 20 ˚С по методу Джонсона и Хуанга
| Атом, группа | Составляющая, кал/(моль·К) | Атом, группа | Составляющая, кал/(моль·К) | ||
| -СН3 | 9,9 | ׀ С=О ׀ | 14,7 | ||
| -СН2- | 6,3 | -СN | 3,9 | ||
| ׀ -СН ׀ | 5,4 | -ОН | 11,0 | ||
| -NH2 | 15,2 | ||||
| -СООН | 19,1 | -Cl | 8,6 | ||
| -СОО- (сложные эфиры) | 14,5 | -Br | 3,7 | ||
| НСОО- (муравьиная кислота и её эфиры) | 3,55 | -O- (простые эфиры)
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2017-12-29 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |