Связь между базисами линейного пространства. Матрица перехода от базиса к базису

Рассмотрим линейное n-мерное пространство V и два произвольных базиса этого пространства:

e₁,e₂,…,e_n, (1)

f₁,f₂,…,f_n. (2)

Так как векторы системы (1) образуют базис, то любой вектор линейного пространства можно выразить как линейную комбинацию векторов этой системы, в том числе и векторы системы (2):

f₁=a₁₁e₁+a₁₂e₂+…+a_1ne_n

f₂=a₂₁e₁+a₂₂e₂+…+a_2ne_n

……………………….., (3)

f_n=a_n1e₁+a_n2e₂+…+a_nne_n

где a_ijÎR.

Составим из коэффициентов матрицу

T= .

Эту матрицу будем называть матрицей перехода от базиса (1) к базису (2). Соотношение (3) можно переписать в матричном виде

(4)

или, если обозначить матрицы 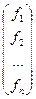=f, =e, тогда в виде

f=Te (5)

Теорема. Матрица перехода от базиса к базису есть невырожденная матрица.

Доказательство

Так как векторы системы (2) – базис линейного пространства, то, аналогично, векторы системы (1) можно представить как линейные комбинации векторов системы (2), то есть можно записать

e =T₁f. (6)

Т₁ – матрица перехода от базиса (2) к базису (1). Тогда из соотношений (5) и (6) получаем

e=T₁f= T₁(Te)=(T₁T)e (7)

и f=Te=T(T₁f)= (TT₁)f. (7’)

Обозначим матрицу T₁T=S с элементами s_ij, тогда равенство (7) можно переписать в виде e=Se или

= Û

e₁=s₁₁e₁+s₁₂e₂+…+s_1ne_n

e₂=s₂₁e₁+s₂₂e₂+…+s_2ne_n

…………………………. (8)

e_n=s_n1e₁+s_n2e₂+…+s_nne_n

Так как V – абелева группа по сложению, то соотношения (8) можно преобразовать к виду

(s₁₁ -1)e₁+s₁₂e₂+…+s_1ne_n=0

s₂₁e₁+(s₂₂ -1)e₂+…+s_2ne_n=0

………………………… (9)

s_n1e₁+s_n2e₂+…+(s_nn -1)e_n=0

Так как система векторов (1) – базис, то есть она является максимальной линейно независимой, то из соотношений (9) получаем

s_ij=0 "i¹j

s_ij=1 "i=j,

то есть матрица

S= =EÞ T₁T= E. (10)

По теореме об определителе произведения матриц, получим

½T₁T½=½T₁½½T½=½E½=1 ½Т½¹0 и ½T₁½¹0.

кроме того, из соотношения (10) следует, что матрицы T₁ и T взаимно обратные. Теорема доказана.

Теорема. Пусть V – n-мерное линейное пространство, тогда всякая квадратная невырожденная матрица порядка n есть матрица перехода от некоторого базиса пространства V к другому базису этого же пространства.

Доказательство. Пусть Т=(а_ij) – невырожденная квадратная матрица порядка n. Пусть e₁,e₂,…,e_n – некоторый базис этого пространства. Умножив справа матрицу Т на матрицу столбец

e= ,

получим соотношение вида (5), а, проведя необходимые преобразования, получим соотношение вида (3). Осталось показать, что полученная таким образом система векторов f₁,f₂,…,f_n образует базис линейного пространства. Так как эта система состоит из n векторов, то достаточно показать, что она линейно независима. Предположим противное, пусть система векторов f₁, f₂, …, f_n - линейно зависима, то есть существуют такие действительные числа l₁, l₂,…, l_n, что выполняются соотношения

l₁ f₁+l₂ f₂+…+l_n f_n= 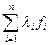=0 (11)

и l₁² +l₂² +…+l_n ²¹ 0. С другой стороны, из соотношения (3) имеем

f_i= . Подставляя это выражение в соотношение (11), получим

=0 и l₁² +l₂² +…+l_n ²¹ 0.

Изменив порядок суммирования, получим

=0.

Так как векторы e₁,e₂,…,e_n – базис, то

=0 "j=1,2,…,n

Это соотношение говорит о том, что между строками матрицы Т существует линейная зависимость, то есть определитель Т равен 0, что противоречит условию. Следовательно, наше предположение неверно, и векторы f₁,f₂,…,f_n образуют базис линейного пространства, что и требовалось доказать.