Интерполяционные квадратурные формулы.

Рассмотрим вычисление следующего интеграла:

, (4)

Где , заданная интегрируемая функция, так называемая весовая функция и - некоторая достаточно гладкая функция, которую назовем подынтегральной. Этот интеграл является более общим по сравнению с рассматриваемым ранее интегралом (1).Интеграл вида (1) получается из (4) при весовой функции .

Для вычисления интеграла (3) применим следующий подход: выберем на отрезке точек . В отличии от предыдущих методов не будем вычислять интегралы на частичных отрезках, а заменим подынтегральную функцию на всем отрезке интерполяционным полиномом Лагранжа, построенным на узлах . В результате получим следующую квадратурную формулу:

(5)

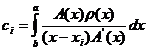
(6)

Формула (5), в которой коэффициенты определяются выражением (6) называется интерполяционной квадратурной формулой.

Абсолютная погрешность формулы (3)оценивается выражением:

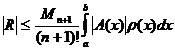(7)

Из выражения (6) видно, что полученная интерполяционная квадратурная формула точна для полиномов - ой степени, поскольку в этом случае .

Таким образом, квадратурная формула интерполяционного типа (5), построенная на узлах является точной для полиномов степени.

Рассмотренные нами ранее формулы прямоугольников, трапеций, Симпсона являются частным случаем квадратурных формул интерполяционного типа при (1, 2 и 3 узла соответственно).

Для некоторых квадратурных формул оценка погрешности (7) является неточной, т.к. она не учитывает симметрии формул. Например, формула средних прямоугольников точна для полиномов 1- ой степени, а формула Симпсона точна для полиномов третьей степени. Квадратурная формула (2) называется симметричной, если:

1) четно ( - узел, )

2) узлы расположены симметрично относительно середины отрезка , т.е.

, ;

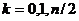3) ,

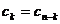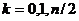
Свойство (3) коэффициентов квадратурной формулы определяется не только симметричным расположением узлов, но и симметрией весовой функции . Говорят, что - четная функция относительно середины отрезка , если

для всех .

Справедлива следующая теорема:

Пусть - четная функция относительно точки и пусть выполнены условия (2), где - четное число. Тогда, если квадратурная формула интерполяционного типа (5) точна для любого многочлена степени , то она точна и для любого многочлена степени .

Заметим, что зависит только от самих узлов, на которые разбит промежуток, но не зависит от функции . Следовательно, коэффициенты не зависят от вида функции также и, используя эти коэффициенты, можно считать интегралы от различных функций (при условии одинакового разбиения на узлы). Т.к. формула (5), построенная на узлах является точной для полиномов степени, то коэффициенты можно найти при помощи метода неопределенных коэффициентов.

Построим интерполяционную квадратурную формулу для вычисления интеграла , . Выберем на стандартном отрезке три равностоящих узла: . Т.к. формула (5) в нашем случае точна для полиномов степени , то имеет место точное равенство для полиномов степени .

На самом деле формула является симметрической (смотри условия симметрии) и верна для полиномов степени , но т.к. у нас три неизвестных коэффициента (три узла), то нам достаточно трех уравнений.