Производная и ее пределы.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И КУЛЬТУРЫТУЛЬСКОЙ ОБЛАСТИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ТУЛЬСКОЙ ОБЛАСТИ

«ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ КОММУНАЛЬНО-СТРОИТЕЛЬНЫЙ ТЕХНИКУМ»

 

Утверждаю

Зам. директора по учебной работе

_________________В. Г. Цибикова

«­­­­_____»__________________2011 г.

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Для домашней контрольной работы

по учебной дисциплине Математика

 

специальности 270802 «Строительство и эксплуатация зданий и сооружений»

семестр 5

форма обучения заочная

 

 

Вопросы рассмотрены на заседании цикловой комиссии «___ »_______________ 2011 г.

Председатель цикловой комиссии _____________________ Преподаватель Кудрявцева О.Б.

Тула 2011

ВВЕДЕНИЕ

Математика относится к числу ведущих наук, в значительной мере определяющих уровень развития научно-технического прогресса общества. Математика и ее методы вторгаются в жизнь людей в самых разнообразных сферах их деятельности, науке, промышленности, сельском хозяйстве, экономике, транспорте, социальной области. Одной из причин широкого применения математики стала повсеместная компьютеризация и использование современных вычислительных средств, взявшие на себя громоздкие расчеты. Но их эффективное использование в значительной мере зависит от математической подготовки пользователя.

Основная цель изучения математики в средних специальных учебных заведениях состоит в том, чтобы дать студентам набор математических знаний и навыков, необходимых для изучения других программных дисциплин, использующих в той или иной мере математику.

Настоящее пособие призвано, в первую очередь, помочь студенту-заочнику 3 курса ТГКСТ в выполнении домашней контрольной работы. Поэтому в нем рассмотрены достаточной подробные решения типовых задач с напоминанием основных положений теории и использованием необходимых формул.

Методические указания к

Домашней контрольной работе

Пределы

Постоянная величина b называется пределом функции ƒ (x) при x стремящемся к x₀ (x→ x₀), если для всех x сколь угодно мало отличающихся от x₀ соответствующие значения функции ƒ (x) сколь угодно мало отличаются от b. То есть, при

x→ x₀ ƒ (x) →b

 

Обозначение:

 

Замечания:

1) x может стремится не только к конечному x₀, но и к бесконечности (x → ∞) и к нулю (x→0).

2) Если , то ƒ (x) называется бесконечно малой функцией при x→0.

3) Если , то ƒ(x) называется бесконечно большой функцией при x→x₀

 

При вычислении пределов используются следующие теоремы:

1. Если функция y= ƒ (x) имеет предел при x→0,то этот предел единственный.

2. Предел постоянной величины равен этой же постоянной, независимо от того, к чему стремится переменная.

, где С= const

3. Предел алгебраической суммы конечного числа функций, имеющих конечные пределы, равен алгебраической сумме пределов всех слагаемых:

4. Предел произведения конечного числа функции, имеющих конечные пределы, равен произведению пределов сомножителей:

5. Предел частного двух функций, имеющих пределы, равен отношению пределов числителя и знаменателя, если предел знаменателя не равен нулю:

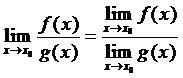, где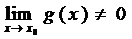

 

6. Постоянный множитель можно выносить за знак предела:

, где С= const

Некоторые виды неопределенностей:

1.

, ,

Например:

 

2.

, ,

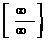
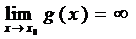
Например:

 

 

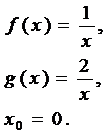
3.

, ,

 

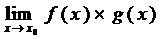Например:

 

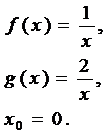
4.

, ,

Например:

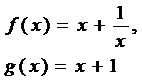
, где c = const

5.

, ,

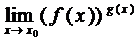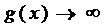
Например:

 

Задача 1.

Вычислить пределы:

a) ;

б) ;

в) ;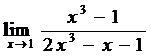

г) ;

 

Решение.

а) Пользуясь теоремами о пределах, получим

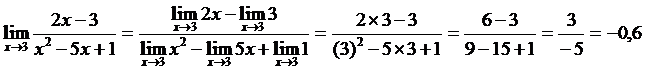
б)

Для того, чтобы раскрыть неопределенность в данном пределе поделим по членно числитель и знаменатель на x в старшей степени в данном выражении, т.е. на x⁴. Получим

в) Применяя теоремы о пределах, обнаруживаем, что ,то есть, знаменатель дроби обращается в нуль. Значит, теорему о предела дроби здесь пока применить нельзя. Но поскольку и предел числителя 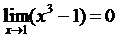, то для того, чтобы раскрыть получившуюся 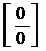неопределенность, мы разложим числитель и знаменатель на множители следующим образом:

Сокращение дроби на (x-1) здесь возможно, поскольку x→1, но x≠1 и множители (x-1) в нуль не обращаются, а являются эквивалентными бесконечно малыми величинами при x→1, отношения которых равно единице.

г) 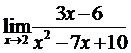Если воспользоваться теоремами о пределах и подставить x=2 в правую часть вместо x, то получим неопределенность 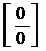. Неопределенность можно устранить, если выделить и сократить эквивалентные бесконечно малые в числителе и знаменателе. Разложим знаменатель на множители, а в числителе вынесем за скобку 3. Получим

 

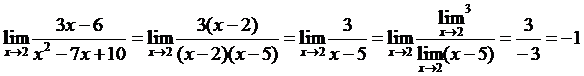
Здесь дробь можно сократить на x-2, так как x→2, но x≠2.

Производная и ее пределы.

Производной функции y= ƒ(x) в точке x называется предел отношения приращения функции ∆y к приращению аргумента ∆x при условии, что ∆x стремится к нулю.

Физический (механический) смысл производной: скорость изменения функции в данный момент времени.

Геометрический смысл производной: значение производной функции y= ƒ(x) в точке x равно угловому коэффициенту касательной проведенной к графику функции в той же точке, т.е.

Функция может иметь производную в точке x=x₀, если она определена в некоторой окрестности этой точки и в самой точке.

Необходимым условием существования производной в данной точке является непрерывность функции в этой точке.

Действие нахождения производной данной функции называется дифференцированием функции. Дифференцирование – однозначная операция.

 

Таблица правил и формул дифференцирования.

Правила дифференцирования.

Формулы дифференцирования.

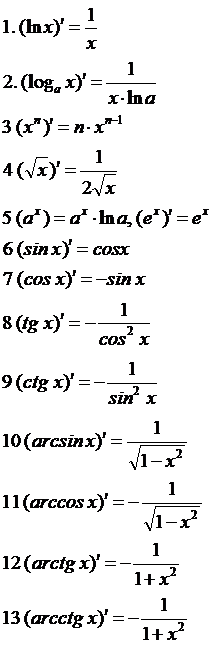
Обратите внимание на понятие дифференциала функции как главной части ее приращения: , причем 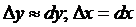, откуда следует,

что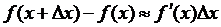

или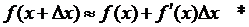

Формулу (*) можно использовать для приближенных вычислений значений функции при небольших изменениях аргумента.

Обратите внимание на связь знака производной на интервале с возрастанием убыванием функции на этом интервале. С этим связано нахождение экстремумов функции (точек максимума и минимума). Точка x=x₀ является точкой экстремума функции 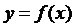, если 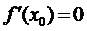или не существует (необходимое условие экстремума).

Достаточным условием экстремума функции в точке x=x₀ является перемена знака ее первой производной при переходе через точку x=x_{0 .}

Производная от первой производной называется второй производной. Ее геометрический смысл – ускорение в данный момент времени, а геометрический смысл – выпуклость или вогнутость графика функции 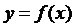в данной точке x.

Задача 2.

Найдите производную функции 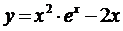и вычислите .

Решение.

Пользуясь правилами дифференцирования, найдем производную

Вычислим

Задача 3.

Найти производную функции и вычислить

Решение.

Ответ:

 

Задача 4.

Исследуйте функцию на экстремум.

Решение.

Найдем производную, приравняем ее к нулю и решим полученное уравнение.

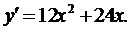
Воспользуемся достаточными признаками экстремума и проверим меняет ли знак первая производная при переходе через критические точки от меньших значений к большим. Здесь первая производная существует при любых значениях x. Оценим знаки производной при x=3, x=-1, x=1:

 

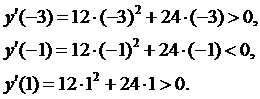
Итак, при переходе слева направо через критическую точку x=-2 производная меняет знак с “+” на “–“, то есть функция слева возрастает, а справа убывает. Значит, x=-2 – точка максимума функции. Найдем ее ординату в этой точке

При переходе слева направо через критическую точку x=0 производная меняет знак с “+” на “-”, следовательно, слева убывает справа возрастает, то есть для нее x=0 – точка минимума, причем .

Ответ: Экстремумы данной функции такие:

 

Задача 5.

Найдите наибольшее и наименьшее значения функции y=x2-x3 на отрезке [-1;3].

Решение. Исследуем функцию на экстремум. Если точки экстремума принадлежат данному отрезку, то вычисляем значения функции в точках экстремума и на концах отрезка и выбираем из них наибольшее и наименьшее.

Итак. Y’=x-x2; x-x2=0, x(1-x)=0.

X1=0; x2=1 –критические точки, причем обе принадлежат отрезку [-1;3]. Вычислим значения функции

Ответ:

Задача 6.

Найдите вторую производную функции 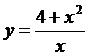и вычислите f’’(4)

Решение. Найдем первую производную, дифференцируя данную функцию как частное:

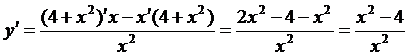
теперь найдем вторую производную аналогично

 

Вычислим

Ответ

Задача 7.

Тело движется прямолинейно по закону s(t)=3t³-4t+2. Найти скорость и ускорение в момент времени t=3.

 

Решение. Если известен закон движения как функция времени, то скорость и ускорение – это соответственно первая и вторая производные по времени, то есть

v=s’(t)=9t²-4, тогда v _t=3=s’(3)=9*3²-4=77.

а= s’’(t)=18t, a_t=3=s’’(3)18*3=54

Задача 8.

Найдите точки перегиба графика функции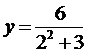

Решение. Для нахождения точек перегиба надо найти вторую производную данной функции, приравнять ее к нулю и решить полученное уравнение. Корни этого уравнения – это критические точки второго рода или точки возможного перегиба. Найдем первую производную

теперь найдем вторую производную

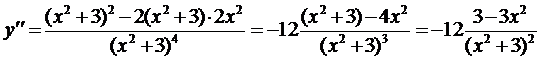
приравнивая вторую производную к нулю, получим уравнение

3-3x²=0

1-x²=0

откуда x_1,2= ±1 – критические точки второго рода.

Проверим, действительно ли точки x= ±1 являются точками перегиба. Поскольку для данной функции

 

то функция четная, значит, если x=1 – точка перегиба, то x= -1 – тоже точка перегиба. Проверим, меняет ли знак вторая производная при переходе через точку x=1. Возьмем, например, x= 0 (-1<0<1) и подставим во вторую производную. Получим : Возьмем теперь x=2, (2>1), тогда , (вычислять не обязательно, достаточно правильно оценить знак). Поскольку вторая производная меняет знак при переходе через точку x=1, то эта точка есть точка перегиба, но тогда и точка x=-1 – тоже точка перегиба.

Ордината обеих точек перегиба будет 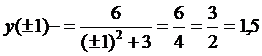, поскольку точки перегиба лежат на самой кривой. Итак, точки N₁(-1;1,5), N₂(1;1,5) – точки перегиба графика данной функции.

Ответ: N₁(-1;1,5), N₂(1;1,5) – точки перегиба/

 

Задача 9.

Постройте график функции

Решение.

Эскизное построение графика можно выполнить по общепринятой в анализе схеме.

1) Найдем область определения функции: x ε(-∞,0) U (0, ∞); x=0 – точка бесконечного разрыва, а прямая x=0 – вертикальная асимптота кривой.

a. Исследуем функцию на четность (нечетность). Вместо x положим –x. Получим 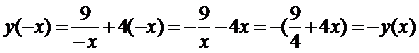, а это признак нечетности функции. Следовательно, ее график центрально симметричен относительно начала координат. Поэтому его можно построить для положительных x и симметрично относительно начала координат перенести для отрицательных x.

2) Найдем точки пересечения графика с осями координат, так называемые “нули” функции. Здесь x≠0, т.к. x=0 не входит в область определения, значит, с осью O y график не пересекается. Пусть y=0, тогда . Это равенство невозможно, так как 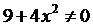при любых значения x. Значит, с осью O y график тоже не пересекается.

3) Найдем точки экстремума и нанесем их на график.

Исследуем характер экстремума в точке

Оценим знаки производной при x=1 и x=2:

, таким образом - абсцисса точки минимума.

Найдем ординату минимума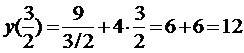

Итак, – точки минимума.

Но тогда, в силу центральной симметрии, точка - точка максимума.

Интервалы монотонности функции:

функция возрастает, если ;

функция убывает, если .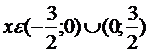

4) Найдем точки перегиба и интервалы выпуклости и вогнутости графика функции ни при каких значениях x вторая производная не обращается в нуль; а в точке разрыва x=0 функция не определена. Следовательно, график не имеет точек перегиба.

Поскольку при x>0 y’’>0, то для x ε(0;∞) кривая вогнутая, а для x ε(-∞;0) (в силу симметрии) – выпуклая.

5) По итогам исследования строим график функции

 

Задача 10.

Вычислить приближенное значение функции y=x³-3x²+30 при изменении аргумента от 3 до 3,002.

Решение. При небольших изменениях аргумента (здесь приращение аргумента ∆x=3,002-3=0,002 небольшое) можно воспользоваться формулой приближенного значения функции f(x₀+∆x)≈f(x₀)+f’(x₀) ∆x. (*).

Примем f(x)=y=x³-3x²+30,

тогда f’(x)=3x²-6x,

положим x₀=3, ∆x=0,002;

Вычислим f(x)=3³-3∙3²+30=30; f’(3)=3∙3²-6∙3=9.

Тогда, по формуле (*) будем иметь f(3,002) ≈30+9∙0,002=30+0,018=30,018.