Пример 1:
Найдите все значения параметра a, при каждом из которых система уравнений 
имеет ровно два решения.
Заменим первое уравнение разностью, а второе – суммой исходных уравнений:
;
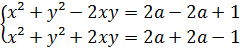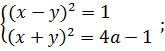
При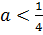 
второе уравнение системы, а, значит, и вся система решений не имеет.
При 
получаем:
;
;
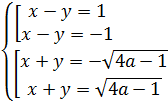Построим графики:
Ясно, что при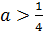 
система имеет четыре решения (координаты точек A, B, C, D), а при 
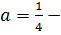два решения (координаты точек M и N).
Ответ: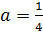 
.
Пример 2:
Найдите все значения параметра a, при каждом из которых уравнение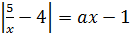 
на промежутке 
имеет более двух корней.
Отметим, что при 
уравнение не имеет положительных корней, так как его левая часть неотрицательна, правая отрицательна. Определим, для каких положительных a график функции 
имеют более двух точек пересечения на области 
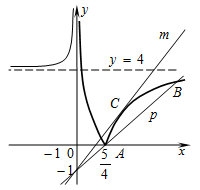
Уравнение 
задает некое количество прямых, проходящих через точку (0;-1). Если их угловой коэффициент меньше, чем у прямой p или больше чем у прямой m, то на промежутке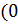 
;+∞) графики будут иметь ровно одну общую точку.
Если прямая совпадает с прямой p или с прямой m, то графики будут иметь ровно две общие точки. Графики имеют три общие точка, а исходное уравнение имеет три положительных решения, если прямые лежат внутри острого угла, образованного прямыми p и m.
Найдем граничные значения параметров, соответствующие этим прямым.
Для прямой p:
.
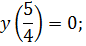
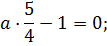
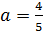Найдем значение параметра, соответствующее касанию.
Касательная к гиперболе имеет с ней единственную общую точку, поэтому дискриминант полученного квадратного уравнения должен быть равен нулю:
.
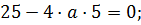
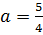Итак, касанию соответствует значение параметра а 
.
При найденных значениях параметров прямая m пересекается с графиком функции 
в точках А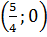 
и В(5; 3), а прямая р касается графика в точке С 
. Замеетим, что точка С действительно лежит левее точки В, в силу того, что график выпукл вверх, и что ордината точки С положительна, иначе оказалось бы, что наш рисунок неверен и потребовалось рассмотреть сообтветствующую конфигурацию.
Тем самым, искомыми значениями параметра являются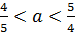 
.
Ответ: .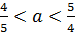
Пример 3:
Найти все положительные значения параметра a, при каждом из которых система 
имеет единственное решение.
Если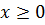 
, то уравнение 
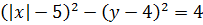задаёт окружность 
, с центром в точке 
радиуса 2, а если 
, то оно задаёт окружность 
с центром в точке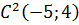 
того же радиуса (см. рисунок).
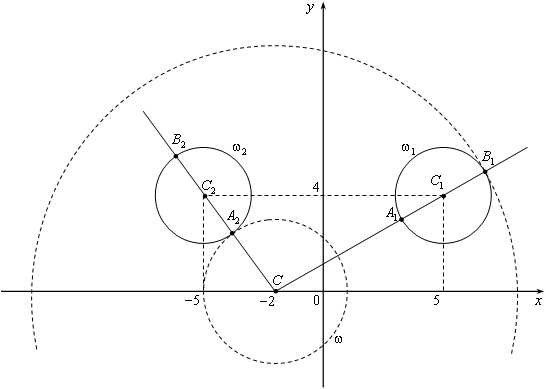
При положительных значениях параметра a уравнение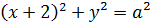 
задаёт окружность 
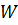с центром в точке 
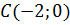радиуса a. Поэтому задача состоит в том, чтобы найти все значения параметра, при каждом из которых окружность 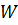имеет единственное общую точку с объединение окружностей и .
Из точки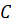 
проведем луч 
и обозначим 
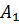и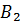 
точки его пересечения с окружностью , где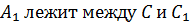 
.
Так как 
, то
.
При 
или 
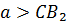окружности 
имеют две общие точки. При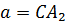 
или 
окружности касаются.
Исходная система имеет единственное решение тогда и только тогда, когда окружность 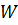касается ровно одной из двух окружностей , и не пересекается с другой. Так как 
, то условию задачи удовлетворяют только числа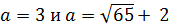 
.
Ответ: 3;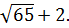 
Задания для тренировки:
1. Найдите все значения параметра a, при каждом из которых уравнение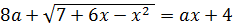 
имеет единственный корень.
2. Найдите все значения параметра a, при каждом из которых уравнение 
не имеет корней.
3. Решите относительно параметра a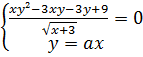 
.
4. Найдите все значения параметра a, при каждом из которых система 
имеет единственное решение/
5.Решите относительно параметра a систему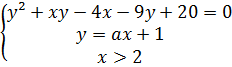 
.