Производная функции.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
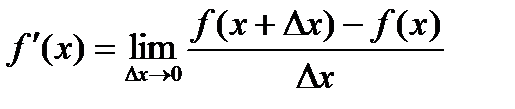
Пример.
Используя определение, найти производную функции 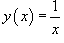 .
.
Решение.
По определению производной
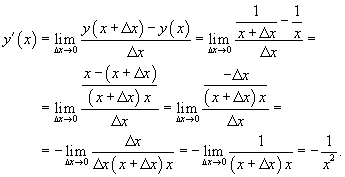
Основные правила дифференцирования.
(u ± v)¢ = u¢ ± v¢
(u×v)¢ = u×v¢ + u¢×v
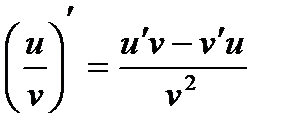 , если v ¹ 0
, если v ¹ 0
Производные основных элементарных функций.
1) С¢ = 0; 9) 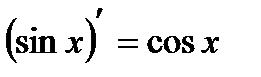
2) (xm)¢ = mxm-1; 10) 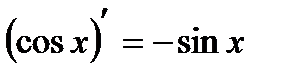
3) 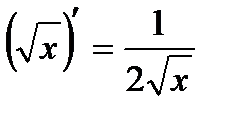 11)
11) 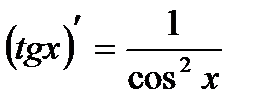
4) 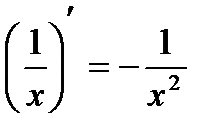 12)
12) 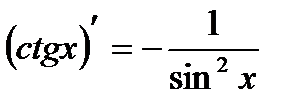
5) 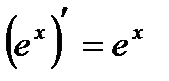 13)
13) 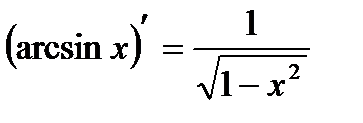
6) 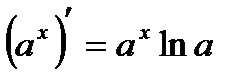 14)
14) 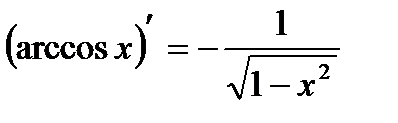
7) 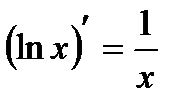 15)
15) 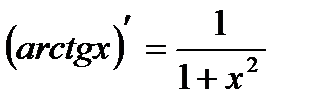
8) 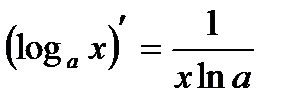 16)
16) 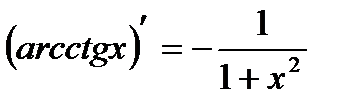
Пример.
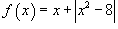 . Найти производную функции в точке x = 3.
. Найти производную функции в точке x = 3.
Решение.
Поскольку 32 - 8 = 1 > 0, то функция в точке x = 3 эквивалентна
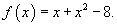
Производная данной функции равна
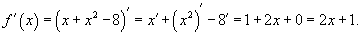
В точке x = 3 значение производной будет
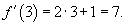
Пример.
Найти производную функции. 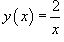
Решение.
Используем правило для вычисления производной частного.
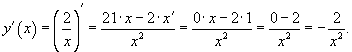
| Пример. |
Пусть 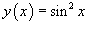 .
Продифференцировать данную функцию, не используя производную сложной функции.
Решение.
Представим функцию в виде y(x) = sinxsinx. По формуле производной произведения .
Продифференцировать данную функцию, не используя производную сложной функции.
Решение.
Представим функцию в виде y(x) = sinxsinx. По формуле производной произведения
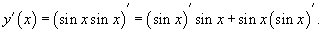 Так как
Так как 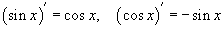 , получаем , получаем
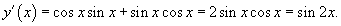
|
Производная сложной функции.
"Двухслойная" сложная функция записывается в виде
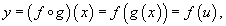
где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.
Если f и g - дифференцируемые функции, то сложная функция 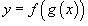 также дифференцируема по x и ее производная равна
также дифференцируема по x и ее производная равна
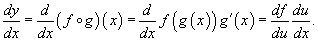
Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f. Тогда 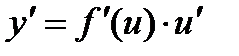
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!
Пример.
Найти производную функции 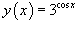 .
.
Решение.
Поскольку 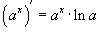 , то по правилу производной сложной функции получаем
, то по правилу производной сложной функции получаем
Пример.
Найти производную 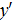 функции у =
функции у = 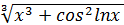 .
.
Решение.
Согласно теореме о дифференцировании сложной функции у = f[u(x)] производная 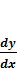 находится следующим образом:
находится следующим образом: 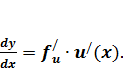
Если у = f [g(u(x))], то у ' = 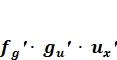 и т. д.
и т. д.
Поэтому производная заданной функции равна:
у′ 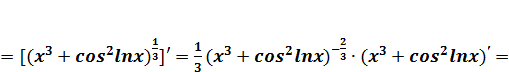
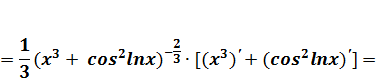
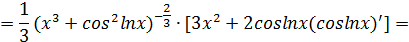
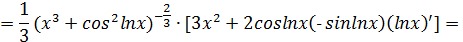
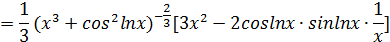
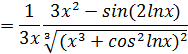
Пример.
Найти производную функции 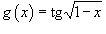 .
.
Решение.
Здесь мы имеем дело с композицией трех функций. Производная тангенса равна 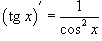 .
.
Тогда
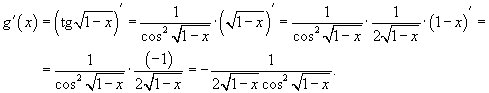
Пример.
Найти производную функции 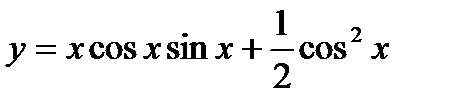 .
.
Решение.
Сначала преобразуем данную функцию: 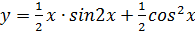
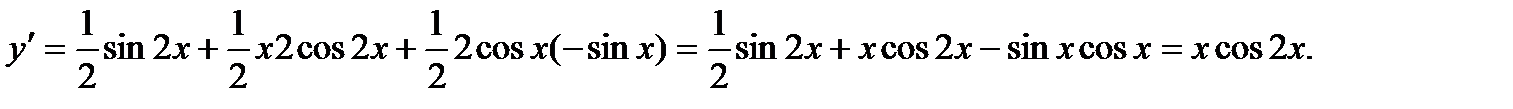
Пример.
Найти производную функции 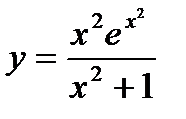 .
.
Решение.
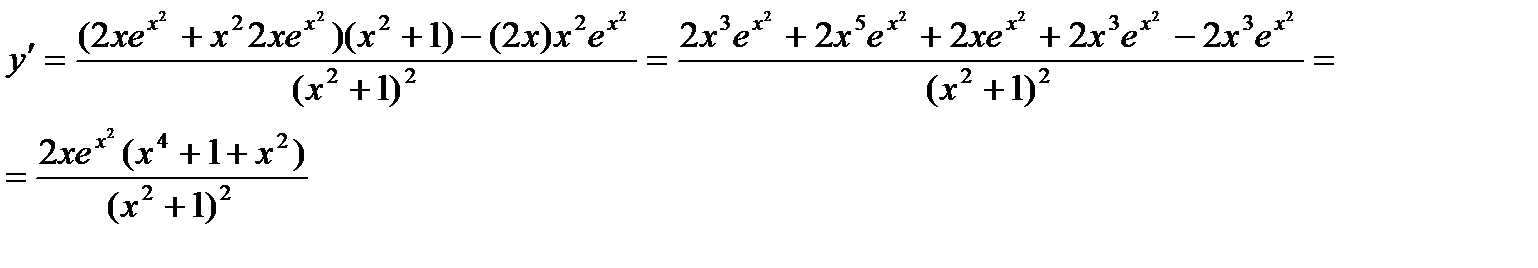
Пример.
Найти производную функции 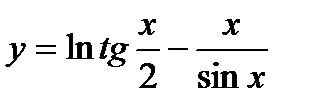
Решение.
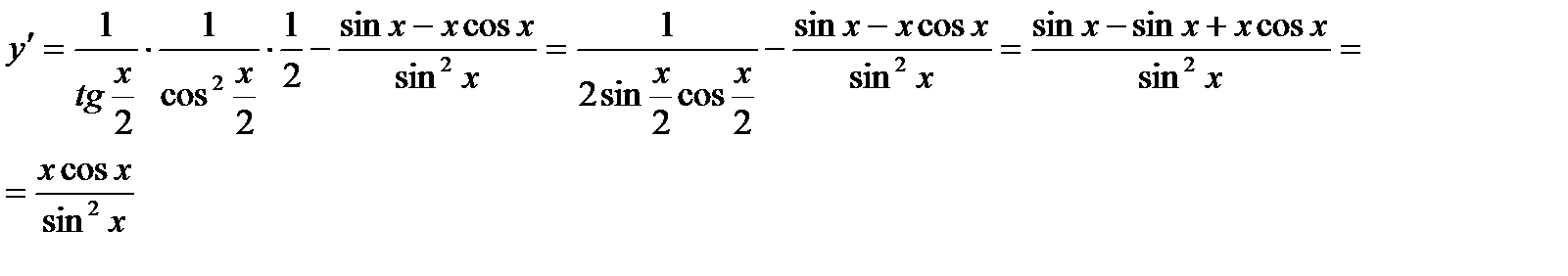
Пример.
Найти производную функции 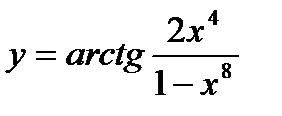
Решение.
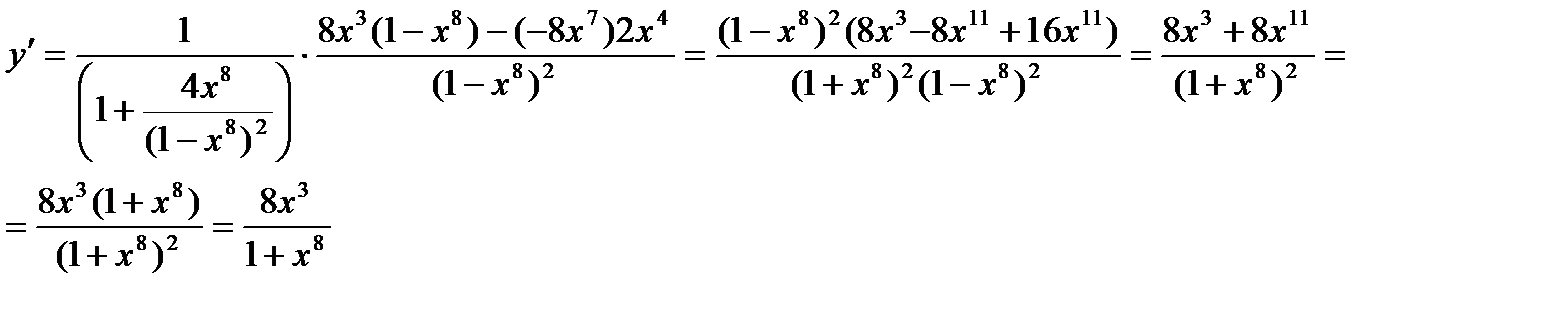
Пример.
Найти производную функции 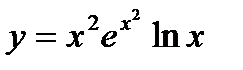
Решение.
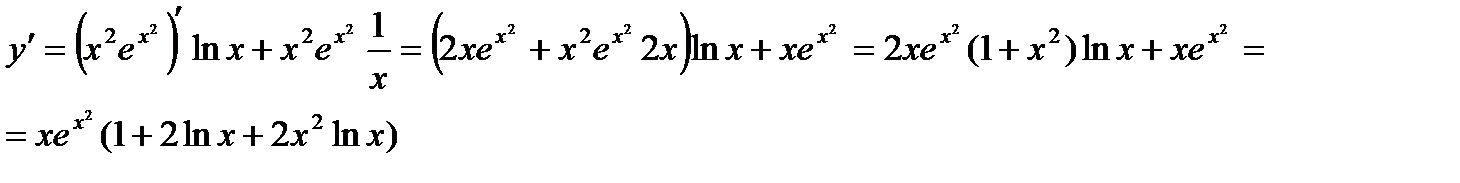
Пример.
Определить производную функции 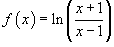 .
.
Решение.
Применим формулы производной сложной функции и производной частного.
Пример.
Продифференцировать функцию 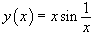 .
.
Решение.
Сначала найдем производную произведения:
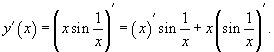
Далее, по формуле производной сложной функции
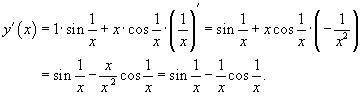
Пример.
Продифференцировать 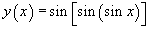 .
.
Решение.
Здесь мы опять имеем дело с "трехслойной" функцией. Поэтому дважды применяем формулу производной сложной функции. Получаем
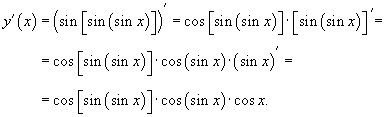
Пример.
Вычислить производную функции 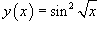 .
.
Решение.
Применим правило производной сложной функции несколько раз.
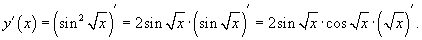
По формуле двойного угла
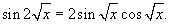
Следовательно, производная равна
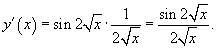
Пример.
Продифференцировать функцию 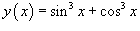 .
.
Решение.
Используем формулы для производной суммы функций и производной степенной функции.
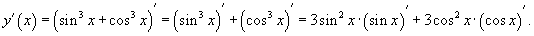
После подстановки производных и упрощения получаем: 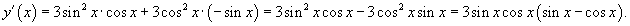
Поскольку 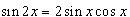 , то окончательное выражение для производной имеет вид
, то окончательное выражение для производной имеет вид
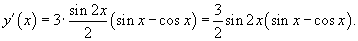
Пример.
Вычислить производную функции 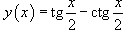 .
.
Решение.
Первый шаг очевиден: 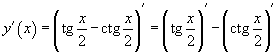
Так как 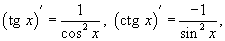
то применяя правило производной для сложной функции, находим:
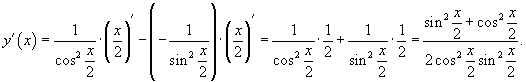
Воспользовавшись для упрощения тригонометрическими формулами 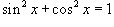 и
и 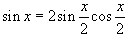 , получаем ответ
, получаем ответ
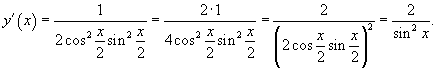
Пример.
Найти производную функции 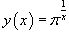 .
.
Решение.
Дифференцируя данную показательную функцию как сложную, находим
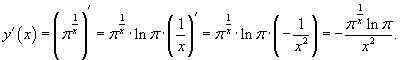
Пример.
Вычислить производную функции 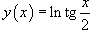 .
.
Решение.
По правилу дифференцирования сложной функции находим
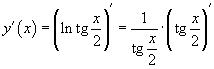
Упрощаем:
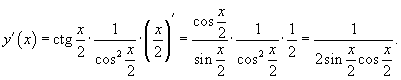
Применив формулу двойного угла 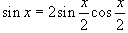 , получаем окончательный ответ
, получаем окончательный ответ
Пример.
Определить производную функции. 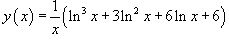
Решение.
Сначала возьмем производную от произведения функций: 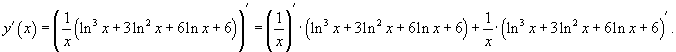
Дифференцируя отдельные члены и упрощая, получаем
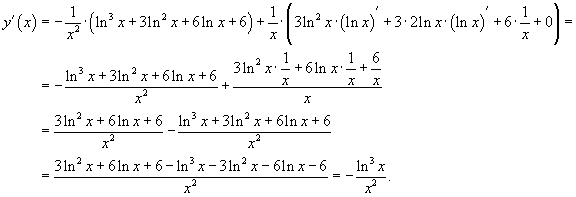
Логарифмическое дифференцирование.
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.
Можно записать 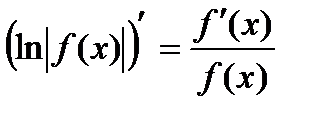 .
.
Отношение 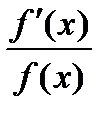 называется логарифмической производной функции f(x).
называется логарифмической производной функции f(x).
Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле
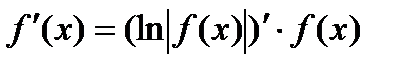
Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
Рассмотрим этот подход более детально.
Пусть дана функция y = f(x).
Возьмем натуральные логарифмы от обеих частей: 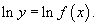
Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.
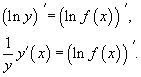
Отсюда видно, что искомая производная равна
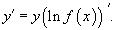
Пример.
Найти производную у' показательно-степенной функции 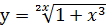 .
.
Решение.
Логарифмируем обе части равенства:
lny 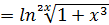
lny 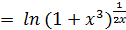
lny 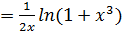
Дифференцируем обе части неравенства. Тогда
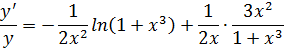
Или окончательно
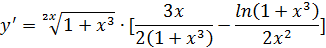
Пример.
Вычислить производную функции 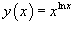 .
.
Решение.
Применяем логарифмическое дифференцирование:
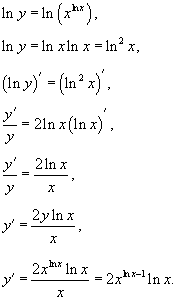
Пример.
Найти производную функции 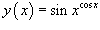 .
.
Решение.
Прологарифмируем обе части и затем продифференцируем.
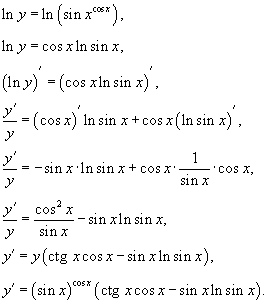
Пример.
Вычислить производную функции 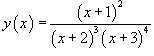 .
.
Решение.
Возьмем логарифм от обеих частей:
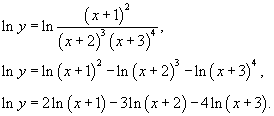
Теперь продифференцируем левую и правую части:
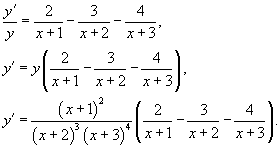
Формула для производной показательно-степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.
Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu
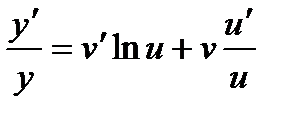
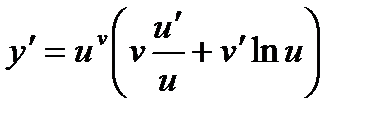
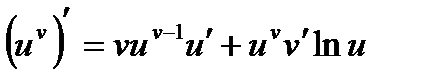
Пример.
Найти производную функции 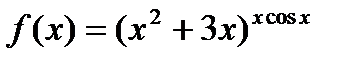 .
.
Решение.
По полученной выше формуле получаем: 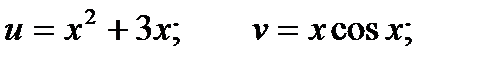
Производные этих функций: 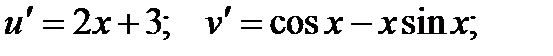
Окончательно:
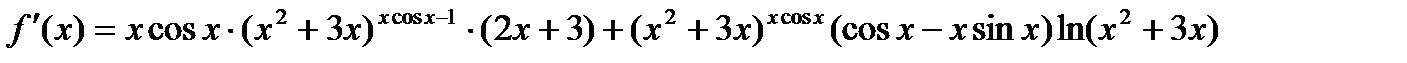
Производная обратных функций.
Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.
Для решения этой задачи дифференцируем функцию x = g(y) по х:
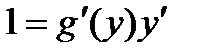
т.к. g¢(y) ¹ 0 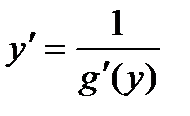
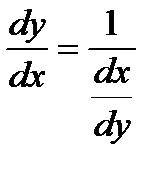
т.е. производная обратной функции обратна по величине производной данной функции.
Пример.
Найти производную 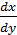 обратной функции
обратной функции 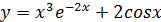 .
.
Решение.
Производные прямой у = f(x) и обратной х = g(y) функций связаны соотношением:
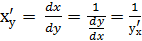 (при условии
(при условии 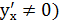
Поэтому сначала находим производную 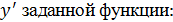
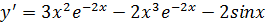
Тогда производная обратной функции равна
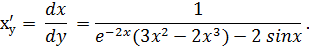
Пример.
Найти формулу для производной функции arctgх.
Решение.
Функция arctgх является функцией, обратной функции tgх, т.е. ее производная может быть найдена следующим образом: 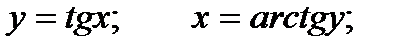
Известно, что 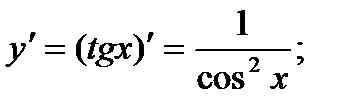
По приведенной выше формуле получаем:
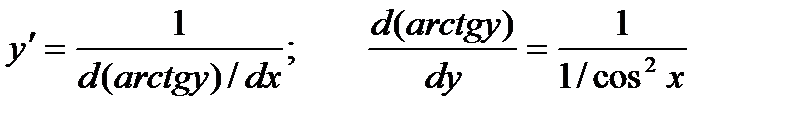
Т.к. 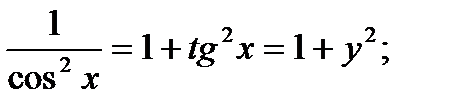 то можно записать окончательную формулу для производной арктангенса:
то можно записать окончательную формулу для производной арктангенса:
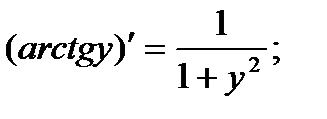
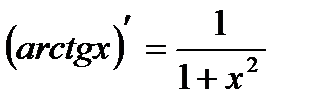
Производная неявных функций.
Во многих задачах функция y(x) задана неявным образом.
Например, для приведенных ниже функций
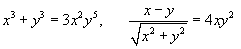
невозможно получить зависимость y(x) в явном виде.
Алгоритм вычисления производной y'(x) от неявной функции выглядит следующим образом:
- Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;
- Решить полученное уравнение относительно производной y'(x).
Пример.
Продифференцировать функцию y(x), заданную уравнением 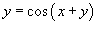 .
.
Решение.
Продифференцируем обе части уравнения по переменной x:
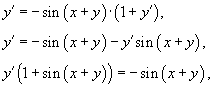
что приводит к результату
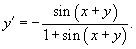
Пример.
Найти производную функции, заданной неявно: 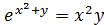 .
.
Решение.
Для того, чтобы найти производную функции у(х), заданной неявно, достаточно продифференцировать правую и левую части уравнения по х, учитывая, что у есть функция от х. Таким образом, получим:
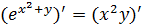
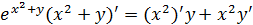
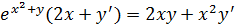
Выразим из полученного соотношения у':
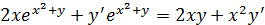
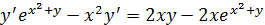
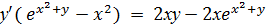
Окончательно получаем:
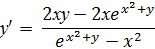
Пример.
Вычислить производную функции y(x), заданной уравнением 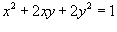 при условии y = 1.
при условии y = 1.
Решение.
Дифференцируем обе части уравнения по x (левую часть дифференцируем как сложную функцию): 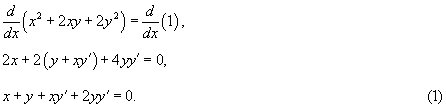
Если y = 1, то из исходного уравнения находим
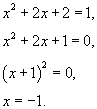
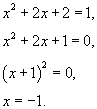
Подставим в уравнение (1) значения x = −1 и y = 1. В результате получаем
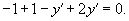
Отсюда следует, что y' = 0 при y = 1.
Производная параметрических функций.
Пример.
Найти производные первого и второго порядка функции заданной параметрически: 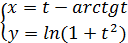
 .
.
Решение.
Производные параметрически заданной функции x=x(t); y=y(t), вычисляются по формулам: 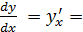
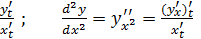
Так как 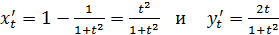
то
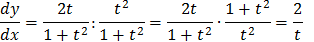
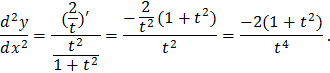
Понятие о дифференциале функции.
Пусть функция y = f(x) имеет производную в точке х:
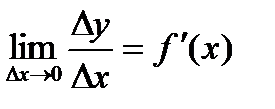
Тогда можно записать: 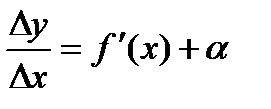 , где a®0, при Dх®0.
, где a®0, при Dх®0.
Следовательно: 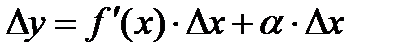 .
.
Величина aDx - бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx - главная часть приращения Dу.
Определение. Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f¢(x)Dx или dy = f¢(x)dx.
Можно также записать: 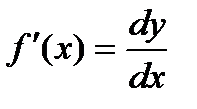
Свойства дифференциала.
Если u=f(x) и v=g(x) - функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
d(u ± v) = du ± dv d(uv) = vdu + udv
d(Cu) = Cdu 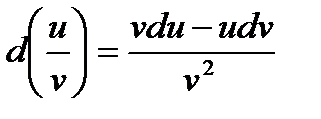
Инвариантная форма записи дифференциала.
Пусть y = f(x), x = g(t), т.е у - сложная функция. Тогда
dy = f¢(x)g¢(t)dt = f¢(x)dx.
Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой-то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
Пример.
Найти дифференциалы 1-го и 2-го порядка функции 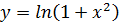 .
.
Решение.
Если x – независимая переменная, то дифференциалы первого и второго порядков функции 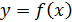 определяется по формулам:
определяется по формулам:
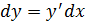 ,
, 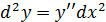
Вычислим производные:
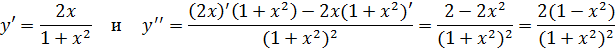
Тогда
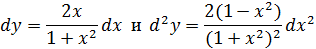
Применение дифференциала к приближенным вычислениям.
Дифференциал функции y = f(x) зависит от Dх и является главной частью приращения Dх.
Также можно воспользоваться формулой 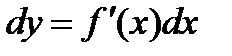
Тогда абсолютная погрешность 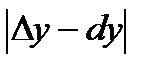
Относительная погрешность 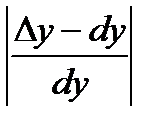
Пример.
Вычислить приближенное значение tg 60°10'.
Решение.
Перейдём к записи угла в радианной мере: 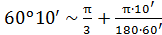
Следовательно, 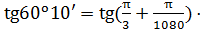
Далее рассмотрим функцию y = tgx.
Условия задачи означают, что надо подсчитать значение функции в точке 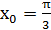 с приращением
с приращением 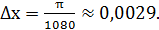
Так как 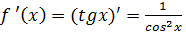 , то имеем:
, то имеем: 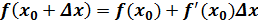
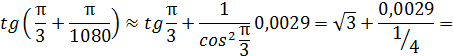
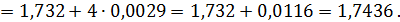
Пример.
Вычислить приближенное значение (2,01)3
Решение.
Рассмотрим функцию у=х3. Необходимо вычислить значение функции в точке х0= 2 с приращением 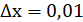 .
.
Тогда 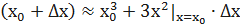 .
.
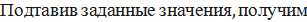
(2,01 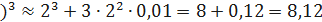 .
.
Уравнение касательной и нормали к кривой.
Уравнение касательной к кривой в точке М0(х0;у0): 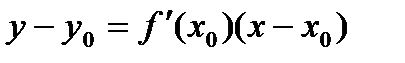
Уравнение нормали к кривой в точке М0(х0;у0): 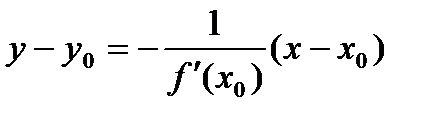 .
.
Пример.
Составить уравнения касательной и нормали к графику функции заданной функции в точке М0:
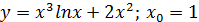
Решение.
Абсцисса точки касания 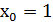 . Для ординаты точки касания нужно
. Для ординаты точки касания нужно 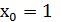 подставить в уравнение функции:
подставить в уравнение функции: 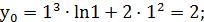 Итак, точка каcания
Итак, точка каcания 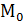 (1; 2).
(1; 2).
Производная 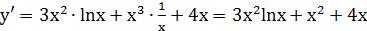 .
.
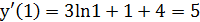
Уравнение касательной: Уравнение нормали:
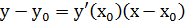
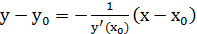
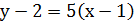
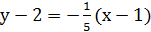
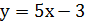
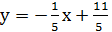
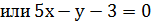
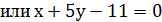
Пример.
Составить уравнения касательной и нормали к графику функции заданной функции в точке М0: 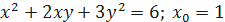
Решение.
При определении углового коэффициента касательной у'(х0) учтём, что функция у = у(х) задана неявно, и, следовательно,
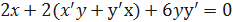
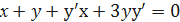
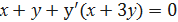
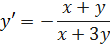
Найдём значение ординаты у0 точки касания из исходного уравнения, подставив в него х0 =1.
Получаем два значения (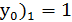 и (
и (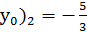 .
.
Угловые коэффициенты соответственно будут 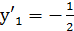 и
и 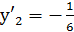 .
.
Тогда в точке M1(1; 1):
уравнение касательной уравнение нормали
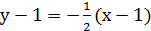
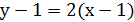
или 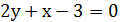 или
или 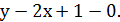
И в точке M2(1; 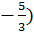 :
:
уравнение касательной уравнение нормали
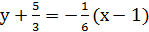
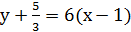
или 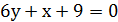 или
или 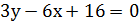
Пример.
Составить уравнения касательной и нормали к графику функции заданной функции 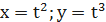 в точке М0 , которой соответствует параметр t0 = 2.
в точке М0 , которой соответствует параметр t0 = 2.
Решение.
В данном примере функция у = у(х) задана параметрически, поэтому, 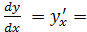
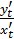 :
: 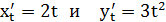
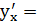
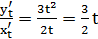 и, следовательно,
и, следовательно, 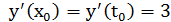 .
.
Так как при 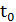 = 2, х0 =
= 2, х0 = 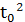 = 4, у0 =
= 4, у0 = 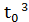 = 8, то
= 8, то
уравнение касательной уравнение нормали
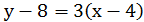
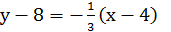
или 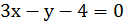 или
или 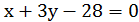
Раскрытие неопределенностей.
Теорема (правило Лопиталя).
Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.
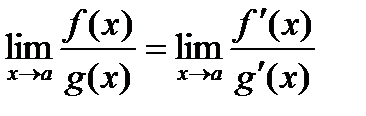
Пример.
Найти предел 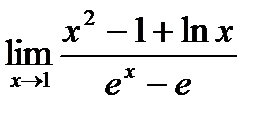 .
.
Решение.
Как видно, при попытке непосредственного вычисления предела получается неопределенность вида 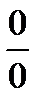 . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
f¢(x) = 2x + 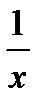 ; g¢(x) = ex;
; g¢(x) = ex;
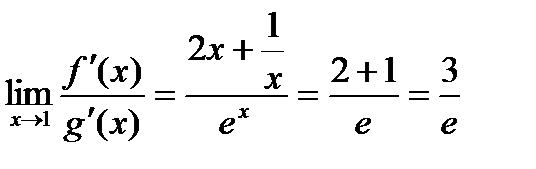 ; ошибка
; ошибка
Пример.
Найти предел 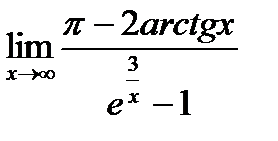 .
.
Решение.
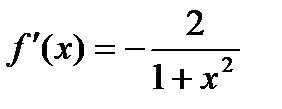 ;
; 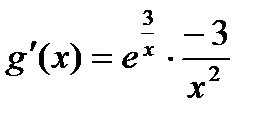 ;
;
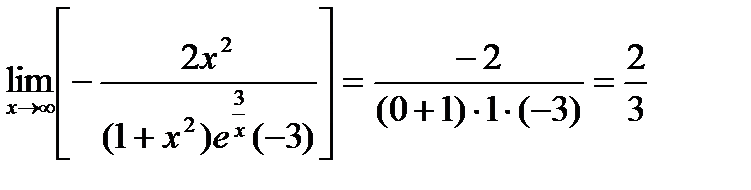 .
.
Пример.
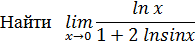
Решение.
В точке x = 0 выражение, стоящее под символом предела есть неопределённость вида 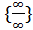 .
.
По правилу Лопиталя находим:
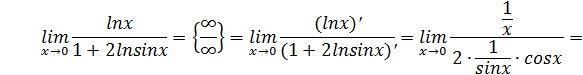
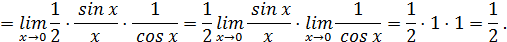
Пример.
Решение.
Выражения f(x)  g(x), представляющие при
g(x), представляющие при  x0 неопределенность вида
x0 неопределенность вида 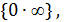 приводится к неопределенности вида
приводится к неопределенности вида 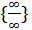 или
или 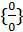 переводом одной из функций в знаменатель. То есть
переводом одной из функций в знаменатель. То есть 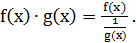 Дальше применяют правило Лопиталя:
Дальше применяют правило Лопиталя:
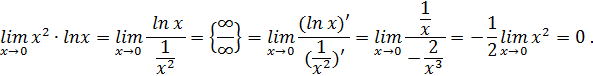
Пример.
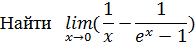
Решение.
Это неопределённость вида 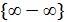 . Для того чтобы найти предел функции, обычно приводят дроби к общему знаменателю, а затем, получив неопределенность вида
. Для того чтобы найти предел функции, обычно приводят дроби к общему знаменателю, а затем, получив неопределенность вида 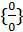 , применяют правило Лопиталя:
, применяют правило Лопиталя:
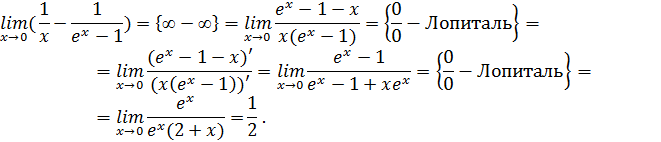
Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
Пример.
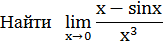
Решение. Так как при  х – sinx = 0 и х3 = 0, имеем так называемую неопределённость вида
х – sinx = 0 и х3 = 0, имеем так называемую неопределённость вида  к которой применимо правило Лопиталя:
к которой применимо правило Лопиталя:
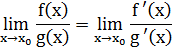
если последний предел существует и 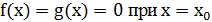 .
.
Итак,
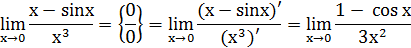
Здесь снова неопределенность вида 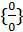 , поэтому применяем правило Лопиталя ещё раз:
, поэтому применяем правило Лопиталя ещё раз:
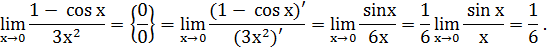
Пример.
Найти предел 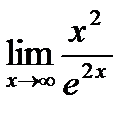 .
.
Решение.
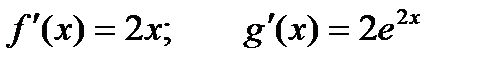 ;
;
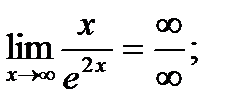 - получили неопределенность.
- получили неопределенность.
Применяем правило Лопиталя еще раз.
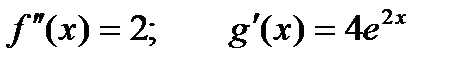 ;
;
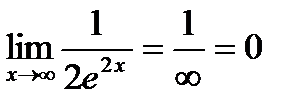 ;
;
Пример.
Найти предел 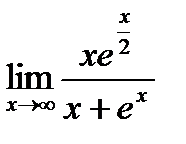 .
.
Решение.
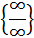
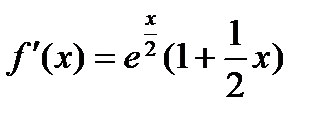 ;
; 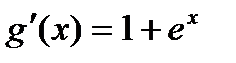 ;
;
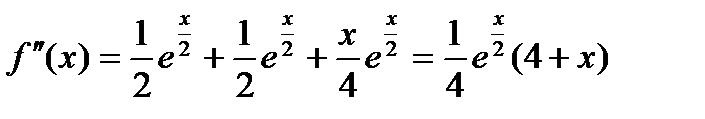 ;
; 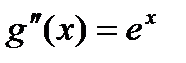 ;
;
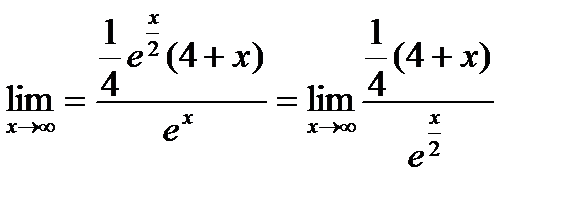
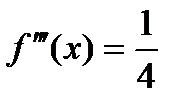 ;
; 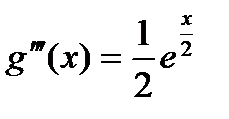 ;
; 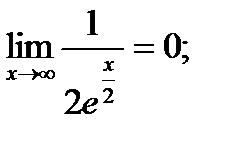
Пример.
Найти предел 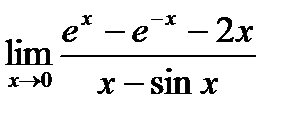 .
.
Решение.
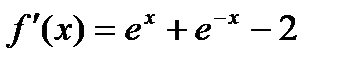 ;
; 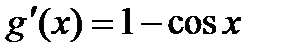 ;
;
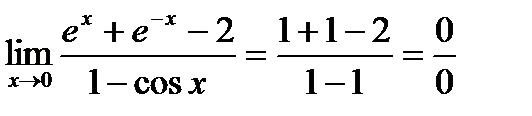 - опять получилась неопределенность.
- опять получилась неопределенность.
Применим правило Лопиталя еще раз.
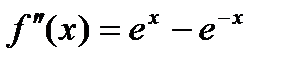 ;
; 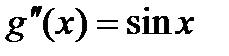 ;
;
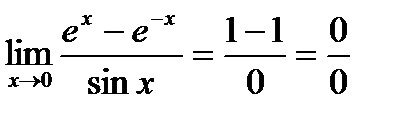 - применяем правило Лопиталя еще раз.
- применяем правило Лопиталя еще раз.
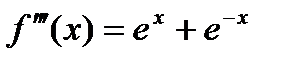 ;
; 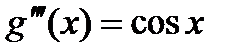 ;
;
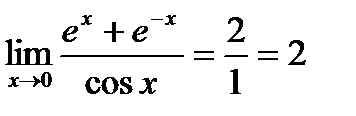 ;
;
Неопределенности вида 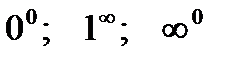 можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида
можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида 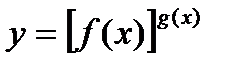 , f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).
, f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).
Пример.
Найти предел 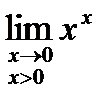 .
.
Решение.
Здесь y = xx, lny = xlnx.
Тогда 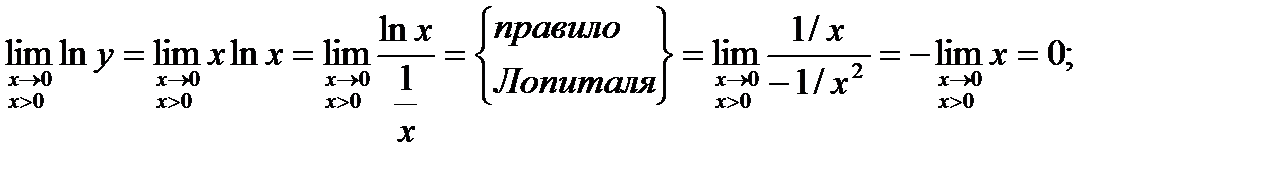 . Следовательно
. Следовательно 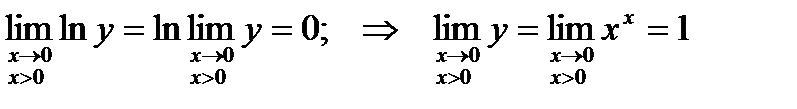
Пример.
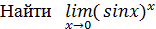
Решение.
Здесь имеется неопределённость вида 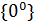 . Преобразуем функцию, стоящую под знаком предела, используя основное логарифмическое тождество
. Преобразуем функцию, стоящую под знаком предела, используя основное логарифмическое тождество 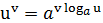 ,
,
то есть
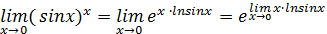
Теперь вычислим предел функции, стоящей в показателе, преобразовав её к неопределённости вида 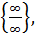 то есть к частному двух функций, и затем применим правило Лопиталя:
то есть к частному двух функций, и затем применим правило Лопиталя:
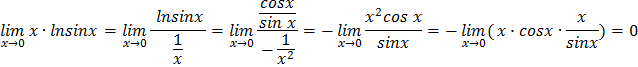
Таким образом,
Производные и дифференциалы высших порядков.
Пусть функция f(x) - дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную
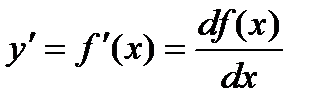
Если найти производную функции f¢(x), получим вторую производную функции f(x).
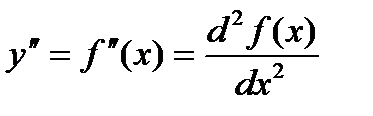
т.е. y¢¢ = (y¢)¢ или 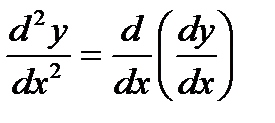 .
.
Этот процесс можно продолжить и далее, находя производные степени n.
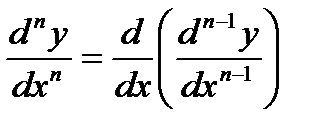 .
.
Общие правила нахождения высших производных.
Если функции u = f(x) и v = g(x) дифференцируемы, то
(Сu)(n) = Cu(n);
(u ± v)(n) = u(n) ± v(n);
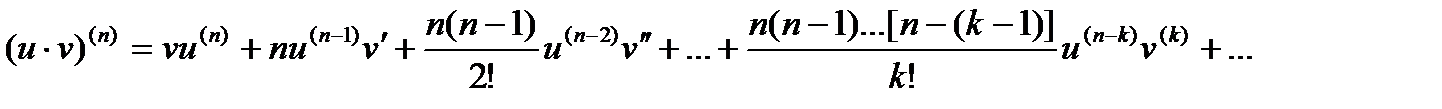
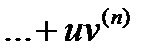 .
.
Это выражение называется формулой Лейбница.
В частности, для производной второго и третьего порядка формула Лейбница принимает вид
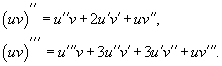
Также по формуле dny = f(n)(x)dxn может быть найден дифференциал n - го порядка.
Пример.
Найти y'', если 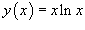 .
.
Решение.
Возьмем первую производную дифференцируя функцию как произведение.
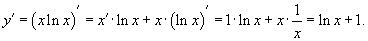
Теперь найдем производную второго порядка
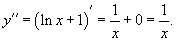
Пример.
Найти у'" от функции у = 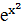 .
.
Решение.
Вычисляем последовательно: 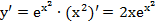
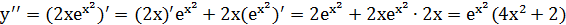
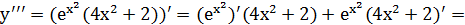
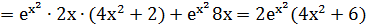
Пример.
Вычислить y'' для