Возрастание и убывание функции.

Приложения дифференциального исчисления функции одной переменной

Рабочая тетрадь

Для самостоятельной работы студентов

Студента(ки) ________________________

гр.____, направление ___________________

Рязань _________ г.

Содержание.

§ 1. Некоторые теоремы о дифференцируемых функциях…………………………..…стр. 3

Теорема Роля.

Теорема Коши.

Теорема Лагранжа.

Правило Лопиталя раскрытия неопределённости вида .

§ 2. Возрастание и убывание функции……………………………………………...…….стр.6

Определения возрастающей и убывающей функции.

Необходимые условия возрастания (убывания) функции.

Достаточные условия возрастания (убывания) функции.

§ 3. Экстремум функции……………………………………………………………………стр.7

Определения максимума и минимума функции.

Необходимые условия экстремума функции.

Определение критических точек первого рода.

Достаточные условия экстремума функции.

§ 4. Выпуклость графика функции, точки перегиба………………………………………стр.10

Определения выпуклости, вогнутости и точки перегиба графика функции.

Теорема (интервалы выпуклости и вогнутости).

Достаточные условия существования точек перегиба.

Определение критических точек второго рода.

§ 5. Общая схема исследования функции и построение графика………………………..стр.12

Список литературы…………………………………………………………………………..стр.13

Некоторые теоремы о дифференцируемых функциях

В основе применения дифференциального исчисления лежат следующие свойства дифференцируемых функций, которые объединены в теоремы.

Теорема 1. (теорема Роля) _______________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Теорему принимаем без доказательств, но поясним её геометрический смысл.

Геометрически теорема Роля означает, что если у функции, гладкой на отрезке 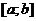, выполняется условие , то________________________________________

Теорема 2. (теорема Коши) _______________________________________________

Теорему принимаем без доказательств.

Теорема 3. (теорема Лагранжа) ___________________________________________

Как и выше, теорему принимаем без доказательств, но поясним её геометрический смысл.

В точке С производная равна тангенсу угла наклона касательной, проведённой в этой точке к графику функции. Т.е. равна угловому коэффициенту этой касательной. Проводим секущую АВ, параллельную касательной. Угловой коэффициент секущей будет равен . Касательная имеет тот же угол наклона, тот же угловой коэффициент. Следовательно,

Пояснить самостоятельно смысл теоремы на следующем графике.

Теорема 4. (Правило Лопиталя раскрытия неопределённости вида )

____________________________________________________________________

Докажем эту теорему, используя теорему Коши.

Теорема 5. (Правило Лопиталя раскрытия неопределённости вида )

____________________________________________________________________

Теорему принимаем без доказательств.

Пример 1. Используя правило Лопиталя найти предел функции .

Решение. .

Пример 2. Используя правило Лопиталя найти предел функции .

Решение.

Замечание: Правило Лопиталя применяют до тех пор, пока не избавятся от неопределённости.

Пример 3. Используя правило Лопиталя найти предел функции .

Решение.

Пример 4. Используя правило Лопиталя найти предел функции .

Решение.

Решить эти же примеры другим способом. Какой способ оказался удобнее?

Возрастание и убывание функции.

Определение. Функция называется возрастающей на , если _______________________________

_____________________________________________________________________________________________

Определение. Функция называется убывающей на , если _______________________________

_______________________________

______________________________________________________________

Убывающая и возрастающая функции называются монотонными функциями.

Теорема 6. (Необходимые условия возрастания (убывания) функции) ______________

Доказательство. Используем для доказательства теоремы геометрический смысл производной. Проведём в произвольных точках несколько касательных к графику возрастающей функции.

Рассмотрим, теперь, убывающую на функцию. Проведём к её графику несколько касательных в произвольных точках.

Теорема 7. (Достаточные условия возрастания (убывания) функции) _____________

Теорему принимаем без доказательств.

Экстремум функции

Определение. Точка 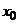называется точкой максимума функции , если____________________________ _______________________________

______________________________________________________________

Определение. Точка 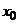называется точкой минимума функции , если____________________________ _______________________________

______________________________________________________________

Значение функции в точке минимума (максимума) называется минимумом (максимумом) функции. Максимум (минимум) функции называется _____________________________

Теорема 8. (Необходимые условия экстремума функции) ______________________

Доказательство.

Геометрически равенство означает__________

____________________________________________________________________________________________________________________________________________________________________________________

Необходимое условие экстремума не является достаточным условием. То есть, если в точке производная функции равна нулю, то это не означает, что в точке существует экстремум функции. Поясним это на примере функции .

Пояснение_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Существуют функции, которые в точках экстремума не имеют производной.

Например, непрерывная функция .

Почему в точке х = 0 функция не имеет производную? ________________________________________________

________________________________________________________________________________________________________________________________________________

Таким образом, непрерывная функция может иметь экстремум в тех точках, где производная равна нулю или не существует.

Определение. Критическими точками первого рода называются ____________________

____________________________________________________________________

Примем без доказательства следующую теорему.

Теорема 9. (Достаточные условия экстремума функции) _______________________

Пример1. Найти интервалы возрастания и убывания и исследовать на экстремум функцию .

Решение. Находим область определения функции:

или . Решив это неравенство методом интервалов, получаем .

Находим критические точки функции, то есть точки, в которых производная равна нулю или не существует.

Производная равна нулю, если числитель равен нулю, отсюда:

, то есть и , . При этом точка не входит в область определения функции и из дальнейшего анализа исключается.

Производная не существует, если знаменатель равен нулю, отсюда:

, то есть или . Получаем: , , .

Отмечаем найденные критические точки на числовой прямой (с учётом области определения заданной функции). Над числовой прямой в выделенных интервалах оцениваем знак производной, под числовой прямой анализируем поведение функции на этих интервалах.

Следовательно, функция в точке 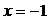имеет экстремум, а именно – максимум:

На интервалах и функция возрастает, на интервале - убывает.

Пример 2. Найти интервалы возрастания и убывания и исследовать на экстремум функцию .

Решение.

Возрастание и убывание функции.

Поиск по сайту