Проверка статистических гипотез

Доверительный интервал для математического ожидания

 

В качестве еще одного примера рассмотрим задачу о доверительном интервале для математического ожидания. Пусть проведено n независимых опытов измерения случайной величины Х с неизвестным математическим ожиданием m_x и дисперсией s². На основании опытных данных Х₁, Х₂,..., Х_n построим выборочные оценки

 

 

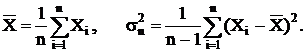
Требуется построить (найти) доверительный интервал l_e, соответствующий доверительной вероятности b, для среднего генерального m_x.

Так как среднее выборочное 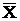представляет сумму n независимых одинаково распределенных случайных величин 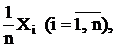то при достаточно большом объеме выборки согласно центральной предельной теоремы ее закон близок к нормальному. Существует эмпирическое правило, по которому при объеме выборки n ³ 30 выборочное распределение можем считать нормальным.

Ранее было показано, что 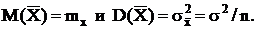Найдем теперь такую величину e(b) > 0, для которой выполняется равенство

 

 

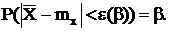
Считая случайную величину 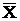нормально распределенной, имеем

 

 

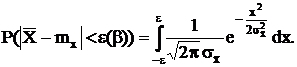
После замены 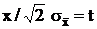имеем

 

 

По табличным значениям функции Лапласа Ф*(z) находим аргумент, при котором она равна b. Если этот аргумент обозначить Z_b, то тогда

 

 

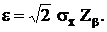
Среднее квадратичное значение 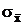приближенно можно заменить

 

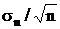
где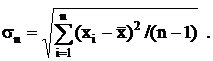

 

Таким образом, доверительный интервал для среднего генерального равен:

l_e =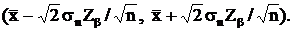

 

Если пользоваться табличными значениями интеграла вероятностей

 

 

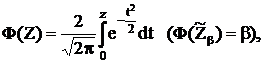
то доверительный интервал принимает вид

 

l_e =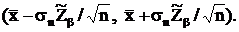

Распределение Стьюдента

 

При малом объеме выборки (n < 30) полученный доверительный интервал для среднего генерального, использующий нормальное распределение случайной величины 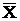, может быть очень грубым.

Для более точного получения доверительного интервала необходимо знать закон распределения случайной величины 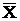при малом объеме выборки. Для этого воспользуемся следующим результатом. Пусть Х₁, Х₂,..., Х_n – выборка нормально распределенной случайной величины Х, тогда, как доказано, случайная величина

 

 

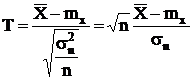
подчиняется распределению Стьюдента c n – 1 степенью свободы, плотность распределения которого имеет вид

 

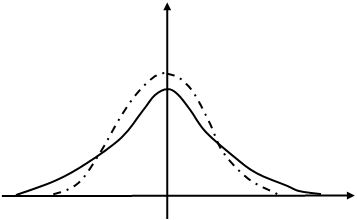
где 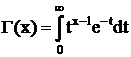- гамма функция. Эта плотность, как видно из формулы, зависит только от числа опытов n. Ниже представлены графики плотностей нормированной (m_x = 0, s = 1) нормально распределенной и с распределением Стьюдента (n = 4) случайных величин.

 

нормальное распределение

f

распределение Стьдента

0,4

0,3

0,2

0,1

-4 -3 -2 -1 1 2 3 4 t

 

На основании найденных 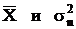можно, пользуясь распределением Стьюдента, найти доверительный интервал для m_x, соответствующий доверительной вероятности b. Действительно, так как 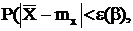то

 

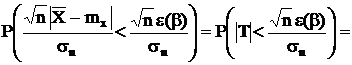
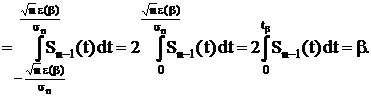
Пользуясь таблицей значений интеграла

 

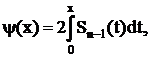
по значению b найдем величину а следовательно, и сам доверительный интервал l_e =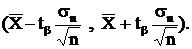

 

Проверка статистических гипотез

Принятие решения о параметрах генеральной совокупности играет исключительно важную роль на практике. Рассмотрим вопрос о принятии решения на примере. Пусть фирма, выпускающая конденсаторы, утверждает, что среднее пробивное напряжение конденсаторов равно или превышает 300 В. Испытав 100 конденсаторов, мы получили, что среднее выборочное пробивное напряжение равно 290 В, а несмещенное выборочное среднее квадратичное отклонение s_n = 40 В. Можно ли с доверительной вероятностью 0,99 утверждать, что среднее пробивное напряжение превышает 300 В.

Здесь нас интересует односторонняя оценка – среднее пробивное напряжение должно превышать 300 В.

Выскажем статистическую гипотезу – генеральное среднее m_x = 300 В, а затем проверим, соответствует ли она результатам наблюдения. Поскольку объем выборки больше 30, то выборочное среднее можно считать гауссовской случайной величиной с генеральной дисперсией s² » s_n². Введем центрированную и нормированную величину

 

 

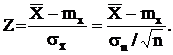
Утверждение о том, что среднее выборочное напряжение эквивалентно утверждению, что случайная величина

 

 

Найдем вероятность того, что гауссовская случайная величина Z с m_z = 0 и s_z = 1 принимает значения больше z_o:

 

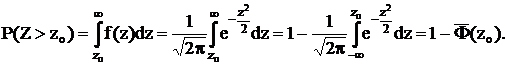
Эта величина должна равняться доверительной вероятности 0,99. Тогда 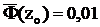и по таблицам значений функции 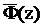находим аргумент z_o = -2,33. Вычислим теперь наблюдаемое значение случайной величины Z:

 

 

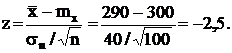
Мы видим, что наблюдаемое значение z = - 2,5 нe принадлежит интервалу [-2,33;¥), поэтому гипотезу нужно отвергнуть.

Приведем пример гипотезы с двухсторонней оценкой. Пусть фирма, выпускающая стабилитроны определенного типа, утверждает, что номинальное напряжение стабилизации стабилитронов равно 10 В. Естественно, что отклонение напряжения стабилизации в меньшую или большую стороны одинаково нежелательно. Выдвинем гипотезу, что генеральное среднее напряжение стабилизации равно 10 В, а затем проверим эту статистическую гипотезу по результатам наблюдения.

Пусть при испытании 100 стабилитронов среднее выборочное равно 10,3 В, а несмещенное выборочное среднее квадратичное отклонение равно 1,2 В. Можно ли с доверительной вероятностью 0,95 считать выдвинутую гипотезу справедливой? Так как объем выборки больше 30, то можно, как и в предыдущем примере, ввести гауссовскую случайную величину Z. Найдем

 

и приравняем правую часть полученного соотношения 0,95. Тогда 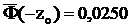и z_o =1,96. Это значит, что наблюдаемое значение z должно принадлежать интервалу (-1,96; 1,96). Поскольку 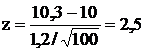не попадает в указанный интервал, то гипотеза отвергается.

Если объем выборки n < 30, то случайная величина 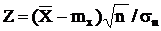cчитается стьюденской случайной величиной T. Поэтому повторяя все указанные выше выкладки для проверки статистических гипотез, значения аргумента ищутся для распределения Стьюдента. При этом, так как "хвосты" стьюденского распределения по отношению к гауссовским удлиняются, доверительные интервалы расширяются, а возможности принятия гипотез улучшаются.

Функция риска