Пример 4. Численное решение уравнений.

> eq:=x^4+2*x^2-2=0;

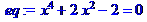
> s:=fsolve(eq,x);

> s:=fsolve(eq,x,complex);

> fsolve(ln(sin(x))=0,x);

> fsolve(ln(sin(x))=0,x,x=2..infinity);

> fsolve(ln(sin(x))=0,x,x=15..infinity);

Здесь также показано, как можно последовательно находить корни про­извольного уравнения, задавая интервал изменения неизвестной величины с учетом полученного решения на предыдущем шаге нахождения корня (последние три команды).

Другие команды решения уравнений.

Кроме универсальных команд solve () и fsolve () решения уравнений и систем уравнений, система Maple содержит специализированные команды, предназначенные либо для решения определенного класса уравнений, либо нахождения решений в заданном числовом поле. Здесь эти команды описаны предельно кратко для того, чтобы читатель знал об их существовании. Более подробно об этих командах можно узнать в справочной системе Maple, выполнив команду?имя_команды, где вместо параметра имя_команды следует подставить ее действительное имя.

Команда isolve () ищет все целые решения уравнений. Если в уравнении задано несколько неизвестных, то строится решение относительно всех за­данных неизвестных.

Пример 5. Целочисленное решение уравнений.

> isolve({(x+1)*(x-1/2)*(x-2)=0});

> isolve({5*x+6*y=1});

Врешении последнего уравнения примера 5 использована целочисленная переменная _Z1 сгенерированная Maple.

Команда msolve () также ищет целочисленные решения уравнения, но только по модулю, заданному вторым параметром.

Пример 6. Целочисленное решение уравнений по заданному целому модулю.

> solve({3*x-4*y=1,7*x+y=2});

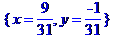
> msolve({3*x-4*y=1,7*x+y=2},11);

> msolve({3^n=4},11);

Команда rsolve () строит общее решение рекуррентного уравнения, используя начальные значения, если они заданы, или через их символьные обозначения, если они не заданы.

Пример 7. Решение рекуррентных уравнений.

> rsolve({F(n+2)=F(n+1)+F(n)},F(n)); # Без начальных условий

> rsolve({F(n+2)=F(n+1)+F(n),F(0)=1,F(1)=1},{F(n)});

# Используя заданные начальные условия

Решение неравенств.

Команда solve () используется для решения неравенств и систем не­равенств в области вещественных чисел точно так же, как и для решения уравнений и систем уравнений. Ответ выражается либо в виде множества неравенств, либо через функции RealRange () иOpen (). Первая определяет замкнутый отрезок действительных чисел, а вторая используется для указа­ния того, что граничная точка не входит в построенное решение. Для задания решения в виде множества, следует задать в виде множества либо само не­равенство, либо неизвестную, относительно которой ищется решение. Если этого не сделать, то ответ будет получен с использованием указанных функ­ций определения действительных отрезков.

Пример 8. Решение неравенств.

> solve((x+3)/(4-x)>4,x);

> solve((x+3)/(4-x)>4,{x});

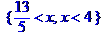
> solve(log[1/2](log[2](x^2-8))>=-1);

> solve({log[1/2](log[2](x^2-8))>=-1});

Впримере 8решены два неравенства, для каждого из которых построено решение в виде множества и в форме действительных интервалов.