Специальностей «география» 012500,
«природопользование» 013400,
«геоэкология» 013600.
Воронеж
Утверждено научно-методическим советом математического факультета Воронежского государственного университета. Протокол №2 от
2 сентября 2003 г.
Составители: Уксусов С.Н., Фетисов Ю.М.
Программа факультета
географии и геоэкологии
ВГУ «учебник студенту»
Учебное пособие «Высшая математика (часть I)» подготовлено на кафедре теории функций и геометрии математического факультета Воронежского государственного университета.
Рекомендовано Ученым советом факультета географии и геоэкологи.
ОГЛАВЛЕНИЕ
Введение……………………..………………………….…………..4
ГЛАВА 1 Элементы линейной алгебры..…….……….….…...5
§1.1. Определитель матрицы.…………………………………….....…………5
§1.2. Метод Крамера решения систем линейных уравнений………………..8
§1.3. Действия над матрицами…………………………………………….…..9
§1.4. Обратная матрица. Решение систем линейных уравнений
матричным способом…………………………………………………...16
§1.5. Решение систем линейных уравнений методом Гаусса……………...20
Глава 2 Элементы векторной алгебры....……….....….….....15
§2.1. Декартова прямоугольная система координат
на плоскости и в пространстве………………………...….……………15
§2.2. Действия над векторами и их свойства…..…….……..……………….17
ГЛАВА 3 Аналитическая геометрия на плоскости…….…...28
§3.1. Простейшие задачи аналитической геометрии……...…..……………28
§3.2. Прямая линия на плоскости………………………….……...………….31
§3.3. Кривые линии второго порядка………………….……………..……...35
ГЛАВА 4 Предел функции. Непрерывность……….……..…50
§4.1. Предел числовой последовательности и функции.
Теоремы о пределах.……………....……………………………….…...52
§4.2. Предел частного двух функций.
Раскрытие неопределенностей вида 
и 
…………..….…...52
§4.3. Первый замечательный предел и следствия из него……………....….55
§4.4. Второй замечательный предел и его следствия…………….………...57
§4.5. Непрерывность функции……..…….……….………….………………60
ГЛАВА 5 Производная функции. Дифференциал………..…61
§5.1. Производная функции. Ее геометрический смысл…..………………64
§5.2. Таблица производных……………………….…………………………66
§5.3. Дифференциал функции, его геометрический смысл
и применение в приближенных вычислениях.…………………….…67
§5.4. Основные правила дифференцирования……..……...………………..70
§5.5. Табличное дифференцирование. Производная обратной функции…69
§5.6. Производная неявной функции и функции, заданной
параметрически. Логарифмическое дифференцирование……………70
§5.7. Производные высших порядков…………………………………….…71
Литература………………………………………………….……76
ВВЕДЕНИЕ
Данное учебно-методическое пособие предназначено для студентов 1-го курса факультета географии и геоэкологии. Высшая математика изучается на факультете в течение двух семестров. В первую часть пособия включены те разделы курса высшей математики, которые входят в программу первого семестра.
Предлагаемое пособие состоит из пяти глав. В первой главе содержатся основные сведения по линейной алгебре. Дается определение определителя и простейшие способы вычисления определителей 2-го, 3-го и n -го порядка. Изучаются матрицы и действия над ними, включая нахождение обратной матрицы. А так же, приводятся три основных метода решения систем линейных уравнений (метод Крамера, метод Гаусса и метод, основанный на использовании матрицы, обратной к основной матрице системы).
Во второй главе изучаются основные вопросы векторной алгебры на плоскости и в пространстве. Рассмотрены простейшие операции над векторами – умножение вектора на число, скалярное векторное и смешанное произведение и их свойства. Приведены формулы вычисления углов между векторами, площадей параллелограммов и треугольников и нахождения объемов параллелепипедов и треугольных пирамид.
В третьей главе пособия решаются простейшие задачи аналитической геометрии на плоскости – нахождение расстояния между двумя точками, деление отрезка в данном отношении и нахождение площади треугольника. Подробно изучаются различные уравнения прямой линии на плоскости. Выведены канонические уравнения кривых второго порядка в декартовой системе координат.
Четвертая глава посвящена изучению теории пределов числовых последовательностей и функций. Доказаны основные теоремы о пределах, приведены стандартные методы раскрытия различных видов неопределенностей, включая методы, основанные на использовании первого и второго замечательного предела и их следствий. Дано определение непрерывности функции. Приведены примеры функций, имеющих точки разрыва первого рода типа «скачок» и «устранимая особенность» и точки разрыва второго рода.
В пятой главе даны определения производной и дифференциала функции и их геометрический смысл. Рассказано о применении дифференциала функции в приближенных вычислениях. Выведены табличные производные и правила дифференцирования. Приведены основные приемы дифференцирования различных функций, включая обратную, неявную функцию и функцию, заданную параметрически. Дано понятие производных высших порядков.
В целях наиболее краткого изложения материала в предлагаемом пособии приведены следующие обозначения:
Символом 2 обозначаются определения различных математических понятий или величин.
Символом g обозначаются теоремы, приводимые в пособии с доказательством. При этом символом 4 обозначается начало доказательства, а символом 3 – окончание доказательства теорем.
Символом 1 обозначаются теоремы, приводимые в пособии без доказательства.
Кроме того, в предлагаемом пособии используются стандартные математические сокращения (кванторы):
квантором Þ обозначается словосочетание «отсюда следует, что»;
квантором Û обозначается словосочетание «тогда и только тогда, когда»;
квантором " обозначается словосочетание «для любого» («для любой»);
квантором $ обозначается слово «существует»;
Глава 1. Элементы линейной алгебры
Определитель матрицы
2 Матрицей называется числовая таблица 
.
Числа 
называются элементами матрицы. Индексы i и j означают, соответственно, номер строки и номер столбца, в которых расположен элемент Число строк, умноженное на число столбцов, называется порядком матрицы. Например, матрица 
является матрицей порядка 3´4. Если число строк матрицы совпадает с числом столбцов
(m = n), то такая матрица называется квадратной (размерности n). В дальнейшем мы будем обозначить матрицы заглавными буквами латинского алфавита (A, B, C, D,…).
Элементы квадратной матрицы, идущие из левого верхнего угла матрицы, в правый нижний угол, называются главной диагональю матрицы. Элементы квадратной матрицы, идущие из левого нижнего угла матрицы, в правый верхний угол, называются вспомогательной диагональю матрицы. Для квадратных матриц вводится понятие определителя.
2 Определителем матрицы второго порядка называется число, вычисляемое по формуле
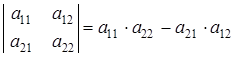. (1.1)
То есть, определитель матрицы второго порядка равен произведению элементов главной диагонали матрицы минус произведение элементов вспомогательной диагонали. Определитель матрицы А обозначается вертикальными прямыми 
или символом det A.
Пример 1.1. Вычислить определитель 
.
Решение. В соответствие с формулой (1.1) получим:
2 Определителем матрицы третьего порядка называется число, вычисляемое по формуле
(1.2)
Одним из методов, позволяющих запомнить громоздкую формулу (1.2) является метод треугольников. Первые три слагаемых, стоящих в правой части формулы (1.2), являются произведениями элементов главной диагонали матрицы и треугольников, одна из сторон которых параллельна главной диагонали 
. Последние три слагаемые берутся с противоположным знаком и являются произведениями элементов вспомогательной диагонали матрицы и треугольников, одна из сторон которых параллельна вспомогательной диагонали .
Пример 1.2. Вычислить определитель третьего порядка: 
.
Решение. Вычислим определитель по формуле (1.2). Получим:
Строгое определение определителя n -го порядка мы приводить не будем, т.к. в нем используется понятие числа инверсий в перестановке, которое нам в дальнейшем не понадобится. Тем не менее, вычислять определители 4-го, 5-го,… порядка мы будем, используя метод разложения определителя по строке или столбцу.
2 Алгебраическим дополнением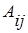 
к элементу квадратной матрицы А называется число, равное определителю матрицы 
(n – 1)-го порядка, полученной из матрицы А путем вычеркивания i -ой строки и
j -го столбца и взятому со знаком плюс, если сумма i+j является четным числом, и со знаком минус, если это число нечетное. Таким образом, алгебраическое дополнение можно найти по формуле:
= 
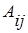×det .
1 Метод разложения определителя по строке или столбцу. Определитель любого порядка равен сумме произведений элементов какой либо строки или столбца на их алгебраические дополнения. Выбирая, например, i -ю строку или j -й столбец мы получим соответственно две формулы для вычисления определителя n -го порядка:
(1.3)
(1.4)
Пример 1.3. Вычислить определитель 
, раскладывая его по первой строке.
Решение. Воспользуемся формулой (1.3), выбрав для разложения определителя первую строку (i = 1):
.
Таким образом,
Вычисляя каждый из определителей третьего порядка по правилу треугольников, получим:
D = (3 + 2 + 10 – 6– 5 –2) – 2×(3 + 5 + 1 – 3 –1 – 5) + 3×(2 + 2 + 5 – 2 –10 – 1) –
– 4×(2 + 2 + 3 – 2 – 6 – 1) = 2 – 12 + 8 = – 2.
Перечислим без доказательства некоторые основные свойства определителя:
Свойство 1. При транспонировании величина определителя не меняется. Транспонированием называется такое преобразование матрицы, при котором строки меняются местами с соответствующими столбцами (первая строка становится первым столбцом вторая строка – вторым столбцом, и т.д.). Другими словами транспонирование – это поворот матрицы вокруг ее главной диагонали. Таким образом:
.
Из первого свойства следует, что все остальные свойства, сформулированные для строк определителя,– справедливы также и для его столбцов.
Свойство 2. Постоянный множитель из любой строки можно выносить за знак определителя:
.
Свойство 3. Если определитель содержит две одинаковые строки, то он равен нулю.
Свойство 4. При перестановке двух строк местами определитель меняет знак на противоположный.
Свойство 5. Если определитель содержит несколько линейно–зависимых строк, то определитель равен нулю. Строки 
, 
,…, 
определителя называются линейно зависимыми, если существуют такие числа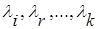 
, не равные нулю одновременно, и такие, что 
.
Выражение вида 
называется линейной комбинацией строк 
.
Свойство 6. Если к произвольной строке определителя прибавить линейную комбинацию других его строк, то величина определителя не изменится.
Пример 1.4. Вычислить определитель 
.
Решение. Используя свойства определителя, приведем матрицу определителя к треугольному виду. Выполним первую серию преобразований: 1) первую строку оставим без изменений; 2) из второй строки вычтем удвоенную первую строку, записав результат во второй строке; 3) к третьей строке прибавим первую строку; 4) вычтем из четвертой строки третью строку, умноженную на 3; 5) из пятой строки вычтем третью строку, умноженную на 5. Тогда получим:
.
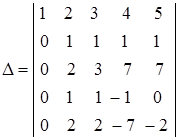Произведем следующую серию преобразований: 1) первую и вторую строку оставим без изменений; 2) из третьей строки вычтем удвоенную вторую строку; 3) из четвертой строки вычтем вторую строку; 5) из пятой строки вычтем четвертую строку, умноженную на 2. Получим
.
Поменяв четвертый и пятый столбец местами и внеся, после этого знак (–) в четвертую строку, получим
.
Наконец, прибавив к пятой строке четвертую строку, умноженную на 2 и затем, раскладывая определитель по первому столбцу, получим:
Метод Крамера решения систем линейных уравнений
Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид
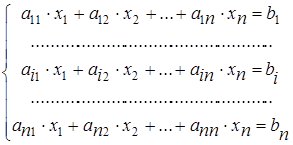. (1.5)
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
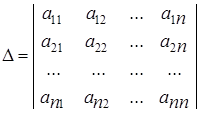. (1.6)
Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
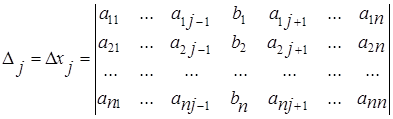(j = 1, 2, …, n). (1.7)
Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:
(1.8)
Пример 1.5. Методом Крамера решить систему уравнений
Решение. Вычислим главный определитель системы:
.
Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):
.
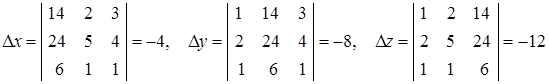Таким образом, 
§1.3. Действия над матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть
2.
. (1.9)
Пример 1.6. 
.
3. Сложение матриц. Данная операция вводится только для матриц одного и того же порядка. Для того, чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. 
.
4. Умножение матриц. Если число столбцов матрицы А совпадает с числом строк матрицы В, то для таких матриц вводится операция произведения:
Таким образом, при умножении матрицы А размерности m ´ n на матрицу В размерности n ´ k мы получаем матрицу С размерности m ´ k. При этом элементы матрицы С вычисляются по следующим формулам:
. (1.11)
Пример 1.8. Найти произведение матриц AB и BA:
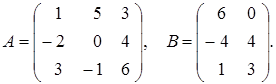
Решение. 1) Для того чтобы найти произведение AB,необходимо строки матрицы A умножить на столбцы матрицы B:
2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A.
§1.4. Обратная матрица. Решение систем линейных
уравнений матричным способом
1. Матрица A- 1 называется обратной к квадратной матрице А, если выполнено равенство:
, (1.12)
где через I обозначается единичная матрица того же порядка, что и матрица А:
.
Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:
, (1.13)
где Aij – алгебраические дополнения к элементам aij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A- 1 к матрице
.
Решение. Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдем det A = | A | = 1×3×8 + 2×5×3 +2×4×3 – 3×3×3 – 1×5×4 – 2×2×8 =
= 24 + 30 + 24 – 27 – 20– 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найдем алгебраические дополнения Aij:
Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A. Таким образом, мы получим обратную матрицу:
2. Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:
, (1.14)
где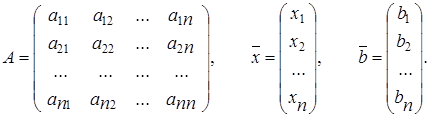 
Умножая обе части равенства (1.14) слева на A- 1, мы получим решение системы:
, откуда
. (1.15)
Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Пример 1.10. Решить систему линейных уравнений
с помощью обратной матрицы.
Решение. Запишем систему в матричном виде: ,
где 
– основная матрица системы, 
– столбец неизвестных и 
– столбец свободных членов. Так как главный определитель системы 
, то основная матрица системы А имеет обратную матрицу А -1. Для нахождения обратной матрицы А -1, вычислим алгебраические дополнения ко всем элементам матрицы А:
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находим по формуле (1.15):
Таким образом, 
§1.5. Решение систем линейных уравнений методом Гаусса
Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:
(1.16)
Найти решения системы или доказать отсутствие решений (расходимость) системы позволяет метод Гаусса. Суть данного метода заключается в том, что с помощью так называемых эквивалентных преобразований система преобразуется к треугольному (трапециидальному) виду. При этом элементы основной матрицы системы, стоящие ниже главной диагонали становятся равными нулю. Затем из последнего уравнения находят одну неизвестную переменную (ту, которая стоит на главной диагонали). Подставляя найденное значение неизвестной в предыдущее уравнение, находят значение второй неизвестной переменной, и т.д.
Назовем эквивалентными преобразованиями такие преобразования системы, при которых система (1.16) не теряет имеющихся у нее решений и не приобретает новых решений. Отметим некоторые из эквивалентных преобразований:
(a) уравнения в системе (1.16) можно менять местами;
(b) любое из уравнений можно умножить на любое отличное от нуля число;
(c) к любому из уравнений системы можно прибавить любое другое уравнение, умноженное на любое число;
(d) к любому из уравнений системы можно прибавить любую линейную комбинацию других уравнений системы.
Пример 1.11. Решить систему линейных уравнений методом Гаусса:
Решение. Так как при эквивалентных преобразованиях изменяются только коэффициенты системы и свободные члены, то решение можно оформлять в матричном виде. Запишем расширенную матрицу системы:
Ко второму уравнению, умноженному на 3, прибавим первое уравнение, умноженное на –2. К третьему уравнению прибавим первое уравнение. Получим:
Поменяем местами второе и третье уравнения, а затем прибавим к третьему уравнению второе, умноженное на – 11:
.
Мы получили систему: 
Из последнего уравнения находим 
.
Подставим z во второе уравнение и найдем y = 13 –15 = –2.
Подставив y и z в первое уравнение, найдем 
.
Пример 1.12. Решить систему линейных уравнений методом Гаусса:
(1.17)
Решение. Запишем расширенную матрицу системы:
.
Ко второму уравнению прибавим первое уравнение, умноженное на –2. К третьему уравнению прибавим первое уравнение, умноженное на –3:
.
Из третьего уравнения вычтем второе уравнение:
.
Таким образом, мы пришли к системе, последнее уравнение которой имеет вид: 0 = 3. Следовательно, исходная система несовместна, т.е. не имеет решений. Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.
Рассмотрим задачу, отличающуюся от задачи (1.17) всего лишь одним свободным членом.
Пример 1.13. Решить систему линейных уравнений методом Гаусса:
(1.18)
Решение. На первом этапе проделаем преобразования аналогичные преобразования предыдущей задачи:
.
Третье уравнение является тождеством, следовательно, его можно исключить из системы. Таким образом, мы приходим к системе двух уравнений с тремя неизвестными:
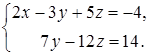
Одну из переменных (например, z) перенесем в правую часть системы, и будем считать параметром. Тогда из второго уравнения находим
.
Подставим y во второе уравнение и найдем x:
Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t:
(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д.
Формулы, позволяющие найти любое решение системы, имеющей бесчисленное множество решений, называются общим решением системы. Формулы (1.19) являются общим решением системы (1.18).
Пример 1.14. Найти общее решение системы линейных уравнений:
Решение. Общее решение системы найдем методом Гаусса, для чего запишем систему в матричном виде:
Здесь символом 
обозначается такое эквивалентное преобразование системы, при котором: 1) из второй строки вычитается первая строка, умноженная на два, и результат записывается во вторую строку; 2) из третьей строки вычитается первая строка, и результат записывается в третью строку. Символом 
обозначается преобразование, которое заключается в следующем: 1) вторая строка умножается на минус единицу, и результат записывается во вторую строку; 2) к третьей строке прибавляется новая вторая строка, и результат записывается в третью строку. Остальные символы расшифровываются аналогично.
Итак, мы получили следующую систему:
Придавая переменным u и v, произвольные действительные значения u = a, v = b, мы получим бесчисленное множество решений.
Итак, 
– общее решение системы.
Пример 1.15. Методом Гаусса решить систему линейных уравнений
Решение. Воспользуемся, как и раньше матричной формой записи системы:
Таким образом, мы пришли к системе уравнений
Из последнего уравнения находим x 4 = 1. Подставляя x 4 в третье уравнение, найдем x 3 = 2 x 4 – 1 = 2 – 1 = 1. Из второго уравнения 
Наконец, из первого уравнения находим 
Итак получено решение
