Уравнение касательной и нормали к графику функции

Известно из школьного курса математики, что уравнение прямой линии, проходящей через точку с координатами и имеющей угловой коэффициент , имеет вид:

(7.1)

Подставляя в эту формулу вместо значениепроизводная функции в точке , получим уравнение касательной к графикуфункции в точке с координатам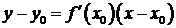и : или .

Определение 7.7. Нормалью к графику функции в точке с координатами называется прямая, перпендикулярная касательной и проходящая через те же точку .

Уравнение нормали к графику функции в точке с координатами получается из уравнения (7.1) прямой линии, имеющей угловой коэффициент , путем замены углового коэффициента

при условии, что .

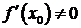Поэтому уравнение нормали имеет вид или .

Правила дифференцирования

Теорема 7.2. Постоянная функция имеет в любой точке производную, равную нулю.

 

Рисунок 7.2 Изображение функции

 

Рассмотрим функцию , её графиком будет прямая линия (см. рис.7.2). Возьмем произвольную точку , лежащую на графике функции. Дадим приращение . Получим точку , тоже лежащую на графике функции. Приращение значений функции будет равно нулю: . Поэтому , что и требовалось.

Теорема 7.3. Если каждая из функций и имеет производную в произвольной точке , то сумма , разность , произведение и частное (при условии ) этих функций тоже имеет производную в этой точке , причем имеют место формулы

1) – производная суммы (разности) двух функций равна сумме (разности) производных каждой функции;

2) – производная произведения двух функций равна сумме производной первого множителя умноженной на второй множитель и первого множителя умноженного на производную второго множителя;

3) – производная частного двух функций равна частному от деления разности производной числителя умноженного на знаменатель и числителя умноженного на производную знаменателя, на квадрат знаменателя.

Следствие 7.1. Из второй формулы получаем свойство: постоянный множитель можно выносить за знак производной, если взять , тогда 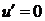, и получаем или .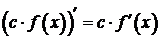

Доказательство формулы производной суммы (разности)

Обозначим .

Тогда .По определению производной и основным теоремах о пределах, получаем

Следствие 7.2. Свойство производной суммы (разности) двух функций можно распространить на любое конечное число функций: производная суммы (разности) функций равна сумме (разности) производных этих функций.

 

Доказательство формулы производной произведения двух функций.

Обозначим .

Тогда . По определению производной и основным теоремах о пределах, получаем

Прибавим и отнимем в числителе произведение , тогда

.

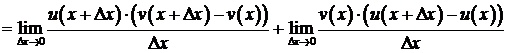Отсюда

, или , что и требовалось.

 

 

Доказательство формулы производной частного двух функций.

Пусть

Отсюда

Прибавим и отнимем в числителе произведение , тогда

 

.

Переходим к пределу при и .

, что и требовалось.

 

 

Таблица дифференцирования основных функций

№	Функция	Производная		№	Функция	Производная
1.			2.
3.			4.
5.

 

Вывод формулы производной степенной функции .

Рассмотрим функцию .

Тогда . Отношение

.

Заменяем бесконечно малый множитель в числителе на эквивалентную бесконечно малую и переходим к пределу при .

Частные случаи к формуле № 1: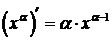

 

№	Значения	Производная	№	Значения	Производная
1.	=1		2.	=2
3.	= –1		4.	=
5.			6.

 

Вывод формулы производной показательной функции . . Рассмотрим функцию ,тогда . Используя свойства показательной функции, преобразуем отношение

Отношение

.

Заменяем бесконечно малый множитель в числителе на эквивалентную бесконечно малую и переходим к пределу при .

.

В частном случае, когда основание показательной функции совпадает с Неперовым числом , то производная , т.к. .

Вывод формулы производной логарифмической функции

при .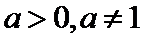

Функция , тогда . Используя свойства логарифмов преобразуем отношение

.

Заменяя числитель на эквивалентную бесконечно малую и переходя к пределу при , получаем

.

В частном случае, когда основание логарифмической функции совпадает с Неперовым числом , то производная , т.к. .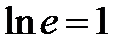

 

Таблица дифференцирования тригонометрических функций

 

№	Функция	Производная		№	Функция	Производная
1.			2.		–
3.				4.

 

Вывод формулы .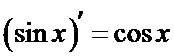

Рассмотрим функцию . Отношение

.

В числителе заменили разность синусов на удвоенное произведение синуса полу-разности и косинус полу-суммы аргументов.

Переходим к пределу при , и учитывая, что , получаем

 

Аналогично, выводится формула .

Рассмотрим функцию .

Отношение

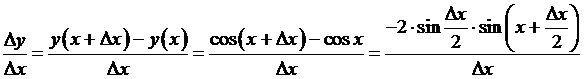
В числителе разность косинусов заменим на удвоенное произведение синуса полу-разности и синус полу-суммы аргументов, взятого со знаком минус.

Переходим к пределу при и учитывая, что , получаем

.

Вывод формулы 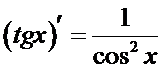осуществляется по правилу дифференцируемости отношения двух функций.

.

Аналогично,