Общая схема исследования функции и построения её графика

При исследовании функции и построении ее графика рекомендуется использовать следующую схему.:

1. Найти область определения функции.

Если область определения функции симметрична относительноначалп координат, то исследовать функцию на четность и нечетность.

Если , то функция четная и график её симметричен относительно оси . Тогда достаточно исследовать только для положительных значений, а далее симметрично отобразить график относительно оси .

Если , то функция нечетная и график её симметричен относительно начала координат. Тогда достаточно исследовать только для положительных значений, а далее симметрично отобразить график относительно начала координат.

Если область определения функции не симметрична относительноначалп координат или не выполняются условия четности или нечетности, тогда функция общего вида и требует исследования при всех допустимых значениях аргумента , как положительных, так и отрицательных.

2. Найти точки пересечения с осями координат и интервалы знакопостоянства функции.

3. Исследовать поведение функции на границе области определения. Найти асимптоты графика функции.

Если , то прямая будет вертикальной асимптотой графика функции.

Если , то прямая будет горизонтальной асимптотой графика функции. Иногда требуется отдельно вычислить предел функции при и при . При конечном значении указанных пределов, существуют левосторонние и правосторонние горизонтальные асимптоты.

Помимо горизонтальных асимптот на бесконечности, у функции могут существовать наклонные асимптоты. Они всегда имеются у функции, представляющей собой отношение двух многочленов, в случае, когда степень числитедя на единицу больше степени знаменателя.

Уравнение наклонных асимптот:

, где , .

Иногда добавляют «Исследовать функцию на непрерывность, найти точки разрыва и выяснить характер разрывов».

 

4. Исследовать функцию с помощью первой производной. Найти интервалы знакопостоянства первой производной и, тем самым, интервалы возрастания и убывания функции и точки экстремума.

5. Исследовать функцию с помощью второй производной Найти интервалы знакопостоянства второй производной и, тем самым, интервалы выпуклости и вогнутости функции и точки перегиба.

6. Эскиз графика функции уточнять по мере исследования и заполнять соответствующую таблицу (см.табл.13.1).

Пример исследования функции и построения её графика

Пример 13.1. Исследовать функцию и построить её график.

Решение.

1.Функция представляет многочлен 3-й степени, поэтому она определена и непрерывна для всех . Область определения функции симметрична относительноначала координат, поэтому исследуем функцию на четность и нечетность

Найдем значение функции при .

или .

Получили и . Следовательно, функция – функция общего вида и ее требуется исследовать на всей числовой оси.

2. Определим точки пересечения функции с координатными осями. Полагая аргумент , находим точку пересечения графика функции с осью ординат : .

Находим точки пересечения функции с осью абсцисс. Записываем:

. Получили уравнение: .

Методом перебора из делителей свободного члена, равного –4 , определяем корнем этого уравнения. Исходим из теоремы Безу: если уравнение с целыми коэффициентами имеет целый корень, то этот корень является делителем свободного члена.

Подставляем в левую часть уравнения. Получаем:

. Поэтому, – корень уравнения.

Подставляем в левую часть уравнения. Получаем:

.

Поэтому, – корень уравнения.

Подставляем в левую часть уравнения. Получаем:

, т.е. не является корнем уравнения.

Чтобы найти третий корень уравнения, разложим левую часть уравнения на множите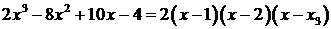ли. или

.

Вынесем общий множитель 2 за скобку в левой части последнего равенства: . Сокращаем обе части равенства на 2. . Приравниваем члены, не содержащие , в правой и левой частях последнего равенства: . Отсюда следует, что . Получили корни уравнения и .

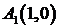Тогда заданная функция имеет 2 точки пересечения с осью абсцисс и .

2.1. Найдем интервалы знакопостоянства функции.

.

Первые два множителя положительны при . Поэтому, знак функции определяется множителем . Если , то ; если , то . Отсюда можно сделать вывод, что функция не пересекает ось в точке , а касается её в точке .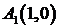

3. Изучим поведение функции на границе области определения и найдём асимптоты графика функции, если они есть.

Функция непрерывна на всей числовой оси, точек разрыва ни первого, ни второго рода не имеет, следовательно, у нее вертикальные асимптоты отсутствуют.

Рассмотрим поведение функции в бесконечности.

Найдем пределы:

и

.

Пределы функции в бесконечности не являются конечными, поэтому горизонтальных асимптот у функции нет.

Проверим наличие у функции наклонных асимптот .

Вычислим предел:

.

Вынесем из множителя в произведении и сократим на в множителе под знаком предела, получим

.

Поскольку предел не является конечными, то наклонные асимптоты отсутствуют.

4. Исследуем функцию с помощью первой производной. Найдем ее производную: .

Производную находим по правилу производной произведения: . Возьмем , тогда . Их производные и . Получаем

.

Вынесем множитель 3 из последнего произведения и сократим с 3 в первом множителе. Тогда

Для нахождения стационарных точек функции приравниваем производную нулю или .

В итоге функция имеет две стационарные точки: .

Находим интервалы знакопостоянства первой производной и, тем самым, интервалы возрастания и убывания функции и точки экстремума.

Используя метод интервалов, найдем интервалы знакопостоянства производной функции .

 

 

Рисунок 13.7. Интервалы знакопостоянства производной функции.

 

При и производная , т.е. интервал являются интервалом возрастания функции.

При производная и интервалом убывания является .

Поскольку при переходе через стационарную точку слева направо производная меняет знак с плюса на минус, то точка является точкой максимума функции .

В другой стационарной точке при переходе слева направо производная меняет знак с минуса на плюс. Следовательно, в точке функция имеет локальный минимум .

5. Исследуем функцию с помощью второй производной Найдем интервалы знакопостоянства второй производной и, тем самым, интервалы выпуклости и вогнутости функции и точки перегиба.

Вычислим вторую производную функции:

Вторая производная определена на всей числовой оси и точки, где она не существует, отсутствуют. Приравнивая вторую производную к нулю, находим . Отсюда точка может быть точкой перегиба.

Для нахождения интервалов выпуклости определяем знак . Если , то . Следовательно, на интервале функция вогнута.

При вторая производная , тогда интервал является интервалом выпуклости функции.

В итоге, поскольку при переходе слева направо точки вторая производная меняет знак, то точка является точкой перегиба функции.

Для удобства построения графика полученные результаты запишем в следующую таблицу (см.табл.13.1).

Таблица 13.1.

Результаты исследования функции

изменения аргумента	изменения функции	Знак производной	Выводы о функции	Фрагмент графика функции
				возрастает и выпукла
				возрастает и выпукла
)				возрастает и выпукла
				Точка максимума
)				убывает и выпукла
				убывает., Точка перегиба
				убывает и вогнута
				Точка минимума
				возрастает и вогнута
				возрастает и вогнута
		+		возрастает и вогнута

 

 

 

Рисунок 13.8. График функции

 

Пример 13.2. Исследовать функцию и построить её график

Решение.

1. Функция определена и непрерывна при всех

Область определения функции симметрична относительно начала координат, поэтому исследуем функцию на четность и нечетность

Найдем значение функции при .

.

Функция нечетна, т.к. . Поэтому график функции симметричен относительно начала координат. Следовательно, достаточно провести исследование в промежутке .

2. Найдем точки пересечения с осями координат и интервалы знакопостоянства функции.

Если , то , и наоборот, если , то . Следовательно, график функции проходит через начало координат.

Интервалы знакопостоянства функции легче искать, если предварительно разложим знаменатель функции на множители, как разность квадратов

По методу интервалов, числовая прямая разбивается на 4 интервала

 

Рисунок 13.9. Метод интервалов

 

Функция положительна при и

отрицательна при .

Исследуем поведение функции на границе области определения и найдем асимптоты графика функции. Заданная функция непрерывность всюду на числовой прямой, за исключением двух точек: . В этих точках у функции разрыв 2 рода (бесконечный).

Найдем предел . Следовательно, прямая - вертикальная асимптота, а значим и по симметрии, прямая - вертикальная асимптота.

Функция, представляет собой отношение двух многочленов, причем степень числитедя на единицу боьше степени знаменателя, поэтому, у функции могут существовать наклонные асимптоты.

Уравнение наклонных асимптот для функции :

, где , .

Вычислим

.

.

Получили: прямая – наклонная асимптота для заданной функции.

3. Найдем точки экстремума функции и установим интервалы монотонности функции.

.

Производную функции находили по правилу вычисления производной дроби, а в конце числитель разложили как разность квадратов.

Находим стационарные точки: . Отсюда 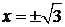. Знак первой производной определяется только произведением: .

 

4. Найти точки перегиба графика функции, определить интервалы выпуклости.

5. Найти точки пересечения с осями координат.

По полученным данным можно построить эскиз графика данной функции. Для примера построим график функции y = 2x³/(x²-4).

1.Область значения функции -  y R.

В промежутке [0,) y обращается в нуль в точках x = 0, x = 2 и обращается в бесконечность в точке x = 2. Отметим, что в интервале [0,2) и (2,2 ) y' меньше нуля и функция убывает, а в интервале (2 ,) больше нуля и следовательно, функция возрастает. Очевидно, что точка x = 2 является точкой минимума.

2.Для нахождения промежутков выпуклости и точек перегиба, найдем вторую производную

y'' = 16 x (x 2+12) / (x 2-4)³.

Вторая производная y'' обращается в нуль в точке x = 0 и в бесконечность в точке x = 2. Ясно, что в интервале (0,2) y'' меньше нуля и поэтому функция выпукла вверх, а в интервале (2,2 ) и (2 ,) y''>0 и функция выпукла вниз. Кроме того, точка x = 0 является точкой перегиба, т.к. вторая производная меняет знак при переходе через эту точку.

3.y(2 ) = 6 , y(0) = 0.

Используя результаты исследования и учитывая нечетность функции, получим график (рис.29).