Методические указания к выполнению индивидуальных домашних заданий по теме: «Функциональные ряды».
Степенные ряды. Сходимость степенных рядов.
 Функциональный ряд вида
Функциональный ряд вида
 , где
, где  - действительные числа, называется степенным рядом.
- действительные числа, называется степенным рядом.
В частности, если  , то мы будем иметь степенной ряд по степеням
, то мы будем иметь степенной ряд по степеням  .
.
Основным свойством степенных рядов является следующее:
Если степенной ряд сходится при  , то он будет сходиться (и притом абсолютно) при всяком значении
, то он будет сходиться (и притом абсолютно) при всяком значении  , удовлетворяющем неравенству
, удовлетворяющем неравенству 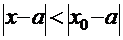 (теорема Абеля).
(теорема Абеля).
Одним из следствий теоремы Абеля является факт существования для всякого степенного ряда интервала сходимости с центром в точке  , внутри которого степенной ряд абсолютно сходится и вне которого ряд расходится. На концах интервала сходимости ряды ведут себя по-разному. Поэтому, в этих точках необходимо проводить дополнительное исследование.
, внутри которого степенной ряд абсолютно сходится и вне которого ряд расходится. На концах интервала сходимости ряды ведут себя по-разному. Поэтому, в этих точках необходимо проводить дополнительное исследование.
Интервал сходимости можно находить, применяя непосредственно признак Даламбера или радикальный признак Коши к ряду, составленному из абсолютных величин членов исходного ряда.
Пример 1.
Исследовать сходимость степенного ряда.
 .
.
Решение. Фиксируем  , получаем числовой ряд и применяем к ряду из абсолютных величин признак Даламбера. Для этого вычислим
, получаем числовой ряд и применяем к ряду из абсолютных величин признак Даламбера. Для этого вычислим

 , если
, если  . Следовательно, ряд расходится, если
. Следовательно, ряд расходится, если  .
.
Ответ:  - точка сходимости.
- точка сходимости.
 .
.
Решение. Применяем к ряду из абсолютных величин признак Даламбера:
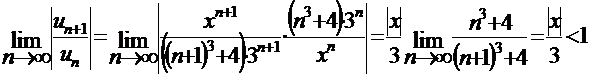 , чтобы ряд сходился. Интервал сходимости найдём из неравенства
, чтобы ряд сходился. Интервал сходимости найдём из неравенства

Проведём дополнительное исследование на концах интервала: в точках  .
.
Подставим  в исходный ряд. Получим знакочередующийся числовой ряд
в исходный ряд. Получим знакочередующийся числовой ряд  . По теореме Лейбница для знакочередующихся рядов этот ряд сходится, так как:
. По теореме Лейбница для знакочередующихся рядов этот ряд сходится, так как:
 .
.
Следовательно, 
 принадлежит интервалу сходимости степенного ряда.
принадлежит интервалу сходимости степенного ряда.
Подставим  в исходный ряд. Получим знакоположительный числовой ряд
в исходный ряд. Получим знакоположительный числовой ряд  , который сравним со сходящимся обобщённым гармоническим рядом
, который сравним со сходящимся обобщённым гармоническим рядом  По 2 признаку сравнения вычислим:
По 2 признаку сравнения вычислим: 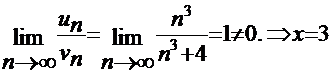 принадлежит интервалу сходимости степенного ряда.
принадлежит интервалу сходимости степенного ряда.
Ответ: интервал сходимости 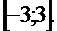

Решение. Фиксируем  и применяем к ряду из абсолютных величин радикальный признак Коши. Вычислим:
и применяем к ряду из абсолютных величин радикальный признак Коши. Вычислим:

Следовательно, ряд сходится при любых значениях  .
.
Ответ: интервал сходимости 
Пример 2.
Исследовать сходимость степенного ряда.

Решение. Фиксируем  и применяем к ряду из абсолютных величин признак Даламбера:
и применяем к ряду из абсолютных величин признак Даламбера: 

чтобы ряд сходился по признаку Даламбера. Интервал сходимости найдём, рассмотрев неравенство: 


Проведём дополнительное исследование на концах интервала: в точках x=0; 2.
Поставим x=0 в исходный ряд. Получим знакочередующийся числовой ряд:

 который сходится по теореме Лейбница, т.к.
который сходится по теореме Лейбница, т.к.
а) 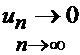 (
( =
= 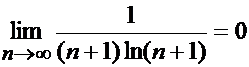 )
)
б)  убывает,
убывает, 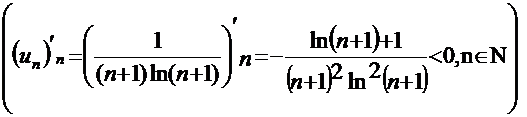 .
.
Следовательно, х=0 принадлежит интервалу сходимости степенного ряда.
Подставим х=2 в исходный ряд. Получим знакоположительный числовой ряд  , который расходится по интегральному признаку Коши, так как несобственный интеграл
, который расходится по интегральному признаку Коши, так как несобственный интеграл 
 - расходящийся.
- расходящийся.
Следовательно х=2 не принадлежит интервалу сходимости степенного ряда.
Ответ: интервал сходимости [0;2).
б) 
Решение. Рассмотрим эквивалентный степенной ряд  , где
, где 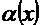 -бесконечномалая при
-бесконечномалая при 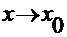 ) Найдём интервал сходимости этого ряда. Применяем к ряду из абсолютных величин признак Даламбера.
) Найдём интервал сходимости этого ряда. Применяем к ряду из абсолютных величин признак Даламбера.
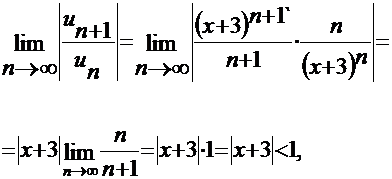
чтобы ряд сходился по признаку Даламбера. Найдем интервал сходимости ряда, рассмотрев неравенство 

 .
.
Проведём дополнительное исследование на концах интервала: в точках х=-4; -2. Подставим х=-4 в исходный ряд. Получим знакочередующийся числовой ряд  , который сходится по теореме Лейбница, т.к.
, который сходится по теореме Лейбница, т.к.
a) 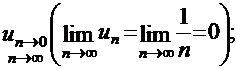
b)  .
.
Следовательно, х = - 4 принадлежит интервалу сходимости степенного ряда.
Представим х=-2 в исходный ряд. Получим расходящийся обобщённый гармонический ряд  . Следовательно х = - 2 не принадлежит интервалу сходимости.
. Следовательно х = - 2 не принадлежит интервалу сходимости.
Ответ: Интервал сходимости 
Приближённые вычисления значений функций и определенных интегралов с помощью степенных рядов.
Всякая функция бесконечно дифференцируемая в интервале  может быть разложена в сходящийся к ней в этом интервале бесконечный степенной ряд Маклорена:
может быть разложена в сходящийся к ней в этом интервале бесконечный степенной ряд Маклорена:

где  0<c<x – остаточный член ряда Маклорена.
0<c<x – остаточный член ряда Маклорена.
Приведём разложения в ряд Маклорена следующих функций: 
Для вычисления логарифмов эффективна формула
 ,
,
где остаточный член  .
.
Для вычисления приближённого значения функции f(x) в её разложении в степенной ряд сохраняются первые n членов (n-конечная величина), а остаточные члены отбрасываются. Для оценки погрешности найденного приближенного значения нужно оценить сумму отброшенных членов (остаточный член Rn(x)). Если данный ряд знакоположительный, то остаточный член оценивают непосредственно; если знакочередующийся, члены которого удовлетворяют теореме Лейбница, то используется оценка
 , где
, где 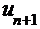 - первый из отброшенных членов ряда.
- первый из отброшенных членов ряда.
Пример 3.
а) Вычислить  с точностью
с точностью 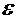 =0,00001.
=0,00001.
Решение. Воспользуемся стандартным расположением  в ряд Маклорена
в ряд Маклорена  и заменим
и заменим  . Получим:
. Получим:

Так как 6-ой член знакочередующегося ряда 
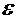 , то это первый отброшенный член.
, то это первый отброшенный член.
Ответ: 0,81873.
б) Вычислить ln2 с точностью 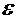 =0.0001.
=0.0001.
Решение.

Остаточный член
 .
.
Путём подбора определим n, что бы выполнялось неравенство 
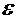


Если n=2 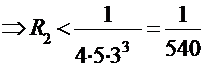 ;
;
Если n=3  ;
;
Если n=4  .
.
Итак n=4 и для определения ln2 получаем приближенное неравенство:

Ответ:0,6931.
Пример 4.
Вычислить с точностью 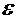 =0,0001 определённый интеграл
=0,0001 определённый интеграл
 .
.
Решение. Заменим в подинтегральном выражении  его разложением в степенной ряд Маклорена:
его разложением в степенной ряд Маклорена:

Т.к. 3 член знакочередующегося ряда меньше заданной точности 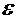 , то это первый отбрасываемый член.
, то это первый отбрасываемый член.
Ответ: 0,2483.