Тема I. Комплексные числа
 ,
,  – действительная часть КЧ,
– действительная часть КЧ,
b – мнимая часть КЧ,
 .
.
Степень мнимой единицы:








 и
и  - комплексно-сопряженные числа.
- комплексно-сопряженные числа.
Действия с КЧ в алгебраической форме:
 и
и 
1.  ;
;
2.  ;
;
3.  ;
;
 ;
;
4. 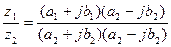 .
.
 - модуль КЧ,
- модуль КЧ,  .
.
 - аргумент комплексного числа, который вычисляется в зависимости от расположения КЧ.
- аргумент комплексного числа, который вычисляется в зависимости от расположения КЧ.
I четверть:  ;
;
II четверть:  ;
;
III четверть:  ;
;
IV четверть: 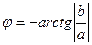 .
.
Если числа расположены на координатных осях:






 - тригонометрическая форма записи КЧ.
- тригонометрическая форма записи КЧ.
Формулы Эйлера:
|
 - показательная форма КЧ.
- показательная форма КЧ.
Действия над КЧ в показательной форме:
1.  ;
;
2.  ;
;
3.  ;
;
4.  , k = 0, 1, 2,…, n – 1.
, k = 0, 1, 2,…, n – 1.
|
Пример 1. Найти модуль комплексного числа и записать число в показательной форме и тригонометрической форме
 .
.
Переведем все числа в показательную форму:
 , т.к.
, т.к.  ,
,  .
.
 , т.к.
, т.к.  ,
,  .
.
 , т.к.
, т.к.  ,
, 
 .
.
Выполним действие:
 .
.
Ответ:  ,
,  ,
,  .
.
Пример 2. Выполнить действия в алгебраической форме, записать число в показательной форме
 .
.
Используем формулу  .
.
 .
.
Найдем модуль и аргумент КЧ:
 ;
;
 ;
;
 .
.
Ответ:  .
.
Пример 3. Выполнить действия в показательной форме, ответ записать в алгебраической форме.
 , если
, если  ,
,  .
.
Переведем число  в показательную форму:
в показательную форму:
 ,
,  ,
,  .
.
Выполним действия:

Ответ: 16.
Пример 4. Найти действительные числа х и у, если

 .
.
Выполним действия в левой и правой части равенства:

 .
.
Используем условие равенства двух комплексных чисел:



Ответ:  .
.
Задание 1.
1.1 Выполнить действия в показательной форме, ответ записать в алгебраической форме:
1.  ; Ответ:
; Ответ:  .
.
2.  ; Ответ:
; Ответ:  .
.
3.  ; Ответ:
; Ответ:  .
.
4. 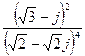 ; Ответ:
; Ответ:  .
.
5.  ,
,  ,
,  ; Ответ: 2.
; Ответ: 2.
6.  ,
,  ,
,  ; Ответ:
; Ответ:  .
.
7.  ; Ответ:
; Ответ:  .
.
8.  ; Ответ:
; Ответ:  .
.
9.  ; Ответ:
; Ответ:  .
.
10.  . Ответ:
. Ответ:  .
.
1.2 Найти модуль комплексного числа и записать число в показательной форме:
1.  ; Ответ:
; Ответ:  .
.
2.  ; Ответ:
; Ответ:  .
.
3.  ; Ответ:
; Ответ:  .
.
4.  ; Ответ:
; Ответ:  .
.
5.  ; Ответ:
; Ответ:  .
.
6.  ; Ответ:
; Ответ:  .
.
7.  ; Ответ:
; Ответ:  .
.
8.  ; Ответ:
; Ответ:  .
.
9.  ; Ответ:
; Ответ:  .
.
10.  . Ответ:
. Ответ: 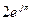 .
.
Тема II. Предел функции
Постоянная b называется пределом функции  при
при  , если для любого числа
, если для любого числа  существует такое число
существует такое число  , что при всех х удовлетворяющих условию
, что при всех х удовлетворяющих условию

выполняется неравенство
 .
.
 |


Если с – постоянная величина, то:
1.  .
.
Если функция  и
и 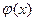 имеют пределы при
имеют пределы при  , то:
, то:
2.  ;
;
3.  ;
;
4.  , если
, если  .
.
Из формулы (3) следует, что:
5.  ,
,  ;
;
6.  ;
;
7.  ,
,  ;
;
8.  ;
;
9. Если существует  и
и  - элементарная функция, то
- элементарная функция, то  .
.
Примеры
1. Найти 
2. Найти 

Правило 1. Чтобы раскрыть неопределенность 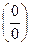 , заданную относительно двух многочленов, необходимо разложить их на множители и сократить.
, заданную относительно двух многочленов, необходимо разложить их на множители и сократить.
3. Найти 


Правило 2. Чтобы раскрыть неопределенность 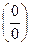 , где присутствуют иррациональные выражения, необходимо числитель и знаменатель дроби домножить на выражения, сопряженные иррациональным и сократить.
, где присутствуют иррациональные выражения, необходимо числитель и знаменатель дроби домножить на выражения, сопряженные иррациональным и сократить.
4. Найти  , так как при
, так как при  величины
величины  и
и  - бесконечно малые, и их пределы равны 0.
- бесконечно малые, и их пределы равны 0.
Правило 3. Если степени числителя и знаменателя равны, то искомый предел равен отношению старших коэффициентов членов дроби.
5. Найти  .
.
Правило 4. Если степень числителя выше степени знаменателя, то при  дробь не имеет конечного предела (предел бесконечный).
дробь не имеет конечного предела (предел бесконечный).
6. Найти  .
.
Правило 5. Если степень числителя ниже степени знаменателя, то  .
.
Чтобы раскрыть неопределенность  нужно числитель и знаменатель дроби разделить почленно на наивысшую степень переменной знаменателя.
нужно числитель и знаменатель дроби разделить почленно на наивысшую степень переменной знаменателя.
7. Найти 

Правило 6. При раскрытии неопределенности  представить выражение в виде дроби, умножить и разделить на выражение, сопряженное иррациональному, далее используя предыдущие правила.
представить выражение в виде дроби, умножить и разделить на выражение, сопряженное иррациональному, далее используя предыдущие правила.
8. Найти 
 .
.
Имеет место соотношение, которое раскрывает неопределенность  :
:
|
Число е – иррациональное ( ).
).
9. Найти  , т.к. если
, т.к. если  .
.
10. Найти  , т.к.
, т.к.
если  .
.
11. Найти 

 ; т.к. если
; т.к. если  , при
, при  ,
,  ,
,  .
.
При вычислении пределов тригонометрических функций часто используется предел отношения синуса дуги к самой дуге.
|
|
или
12. Найти 
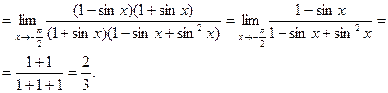
13. Найти 
14. Найти 
 .
.
15. Найти 
 16. Найти
16. Найти 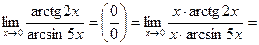

(При  , следовательно
, следовательно  - бесконечно малая функция, пусть
- бесконечно малая функция, пусть  , тогда
, тогда  ,
,  . При
. При 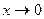 ,
,  ,
,  , пусть
, пусть  , тогда
, тогда  ,
,  ).
).
Задание 2.
2.1 Найти предел функции, не пользуясь правилом Лопиталя:
1.  Ответ:
Ответ:  .
.
2.  Ответ: 0.
Ответ: 0.
3.  Ответ:
Ответ:  .
.
4.  Ответ:
Ответ:  .
.
5.  Ответ:
Ответ:  .
.
6.  Ответ:
Ответ:  .
.
7.  Ответ:
Ответ:  .
.
8.  Ответ:
Ответ:  .
.
9.  Ответ:
Ответ:  .
.
10.  Ответ:
Ответ:  .
.
11.  Ответ:
Ответ:  .
.
12.  Ответ:
Ответ:  .
.
13.  Ответ: 3.
Ответ: 3.
14.  Ответ:
Ответ:  .
.
15.  Ответ:
Ответ:  .
.
16.  Ответ: 4.
Ответ: 4.
17.  Ответ:
Ответ:  .
.
18.  Ответ:
Ответ:  .
.
19.  Ответ: 1,5.
Ответ: 1,5.
20.  Ответ: 0.
Ответ: 0.
21.  Ответ:
Ответ:  .
.
22.  Ответ:
Ответ:  .
.
23.  Ответ: 0.
Ответ: 0.
24.  Ответ:
Ответ: 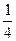 .
.
25.  Ответ:
Ответ:  .
.
26.  Ответ: 6.
Ответ: 6.
27.  Ответ:
Ответ:  .
.
28.  Ответ:
Ответ:  .
.
29.  Ответ: 3.
Ответ: 3.
30.  Ответ:
Ответ:  .
.
31.  Ответ:
Ответ:  .
.
32.  Ответ: 1.
Ответ: 1.
33.  Ответ: 0.
Ответ: 0.
34.  Ответ:
Ответ:  .
.
35.  Ответ:
Ответ:  .
.
36.  Ответ:
Ответ:  .
.
37.  Ответ: 0.
Ответ: 0.
38. 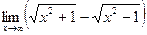 Ответ: 0.
Ответ: 0.
39.  Ответ:
Ответ:  .
.
40.  Ответ: 4.
Ответ: 4.
41.  Ответ:
Ответ:  .
.
42.  Ответ:
Ответ:  .
.
43.  Ответ:
Ответ:  .
.
44.  Ответ:
Ответ:  .
.
45.  Ответ:
Ответ:  .
.
46.  Ответ:
Ответ:  .
.
47.  Ответ:
Ответ:  .
.
48.  Ответ:
Ответ:  .
.
49.  Ответ:
Ответ:  .
.
50.  Ответ:
Ответ:  .
.
51.  Ответ:
Ответ:  .
.
52.  Ответ:
Ответ:  .
.
53.  Ответ:
Ответ:  .
.
54.  Ответ:
Ответ:  .
.
55.  Ответ:
Ответ:  .
.
56.  Ответ:
Ответ:  .
.
57.  Ответ: 2.
Ответ: 2.
58.  Ответ: 8.
Ответ: 8.
59.  Ответ:
Ответ:  .
.
60.  Ответ:
Ответ:  .
.
61.  Ответ: 2.
Ответ: 2.
62.  Ответ:
Ответ:  .
.
63.  Ответ:
Ответ:  .
.
64.  Ответ:
Ответ:  .
.
65.  Ответ: 1.
Ответ: 1.
66.  Ответ: 0.
Ответ: 0.
67.  Ответ:
Ответ:  .
.
68.  Ответ:
Ответ:  .
.
69.  Ответ: 8.
Ответ: 8.
70.  Ответ:
Ответ:  .
.
Тема III. Производная функции и ее приложения
Производная, ее геометрический и физический смысл.
Правила и формулы дифференцирования
Напомним, что приращением функции  называется разность
называется разность
 ,
,
где  - приращение аргумента x.
- приращение аргумента x.
 |
Из рисунка видно, что  . (1)
. (1)
Предел отношения приращения функции  к приращению аргумента
к приращению аргумента  при произвольном стремлении к нулю называется производной функции
при произвольном стремлении к нулю называется производной функции  в точке х и обозначается одним из следующих символов:
в точке х и обозначается одним из следующих символов:  ,
,  ,
,  .
.
Таким образом, по определению
 . (2)
. (2)
Если указанный в формуле предел существует, то функцию  называют дифференцируемой в точке х, а операцию нахождения производной
называют дифференцируемой в точке х, а операцию нахождения производной  - дифференцированием.
- дифференцированием.
Из равенств (1) и (2) следует, что производная в точке х равна тангенсу угла  наклона касательной, проведенной в точке
наклона касательной, проведенной в точке  , к графику функции
, к графику функции  .
.
С физической точки зрения производная  определяет скорость изменения функции в точке х относительно аргумента х (
определяет скорость изменения функции в точке х относительно аргумента х ( - мгновенная скорость,
- мгновенная скорость,  - средняя скорость изменения функции).
- средняя скорость изменения функции).
Если с – постоянное число и  ,
,  - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
- некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  ,
, 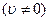 ;
;
7. 
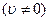 ;
;  ;
;  ;
;
8. Если  ,
,  , т.е.
, т.е.  - сложная функция, то
- сложная функция, то
 или
или  .
.
На основании определения производной и правил дифференцирования можно составить таблицу производных функций:
1.  ,
, 
2.  ,
,  , где
, где 
3.  ,
,  ,
, 
4.  ,
,  ,
, 
5.  ,
, 
6.  ,
, 
7.  ,
,  ,
, 
8.  ,
,  ,
, 
9.  ,
,  ,
, 
10.  ,
,  ,
, 
11. 

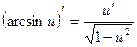
12. 


13.  ,
,  ,
, 
14.  ,
,  ,
, 
15.  ,
,  ,
, 
16.  ,
,  ,
, 
17.  ,
,  ,
, 
18.  ,
,  ,
, 
Уравнение касательной к кривой  в точке
в точке  :
:
 .
.
Уравнение нормали к кривой в точке  :
:
 ,
,  .
.
При  уравнение нормали имеет вид:
уравнение нормали имеет вид:
 .
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым в этой точке, который вычисляется по формуле
 .
.
Примеры
1. Найти производную функции  .
.
Решение:

Ответ: 
2. Найти производную функции  .
.
Решение:
Упростим выражение:

Найдем производную функции:

Ответ: 
3. Найти производную функции  .
.
Решение:
Упростим выражение:
 Найдем производную функции:
Найдем производную функции:


Ответ: 
4. Записать уравнения касательной и нормали к кривой  в точке с абсциссой
в точке с абсциссой  .
.
Решение:
Для составления уравнений касательной и нормали найдем ординату точки М, через которую проходит касательная, и ее угловой коэффициент.
Найдем ординату точки касания, подставив в уравнение кривой значение  :
:
 ;
;  .
.
Вычислим угловые коэффициенты касательной и нормали:
 ;
;
 .
.
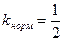 .
.
Найдем уравнение касательной:
 ,
,  ,
,  .
.
Найдем уравнение нормали:
 ,
,  ,
,  .
.
Ответ:  ,
,  .
.
5. Составить уравнение касательной и нормали к эллипсу  в точке
в точке  .
.
Решение:
Дифференцируем уравнение эллипса по х, рассматривая у как функцию от х:
 ,
,  , откуда
, откуда  .
.
Найдем угловые коэффициенты касательной и нормали в точке  :
:
 .
.
 .
.
Уравнение касательной имеет вид:
 ,
,  ,
,  .
.
Уравнение нормали:
 ,
,  ,
,  .
.
Ответ:  ,
,  .
.
6. Вычислить острые углы, образуемые при пересечении парабол  и
и  .
.
Решение:
Найдем точки пересечения парабол. Для этого решим систему уравнений:



Параболы пересекаются в точках О (0;0) и А (1;2).
Угол между двумя пересекающимися параболами найдем как угол между касательными к ним, проведенным в точке пересечения. Вычислим угловые коэффициенты касательных к параболам в точках их пересечения. В точке (0;0) касательными к параболам служат оси ОХ и ОУ, следовательно в этой точке параболы пересекаются под прямым углом.
Для вычисления коэффициента касательной к параболе  в точке А запишем ее уравнение в виде
в точке А запишем ее уравнение в виде  :
:
 ,
,  .
.
Вычислим угловой коэффициент касательной к параболе  в точке А, записав ее уравнение в виде
в точке А, записав ее уравнение в виде  :
:
 ,
,  .
.
Найдем угол между касательными, зная их угловые коэффициенты  и
и  :
:
 ;
;  .
.
7. Закон прямолинейного движения тела задан уравнением 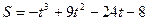 . В какой момент времени скорость движения тела окажется равной 0?
. В какой момент времени скорость движения тела окажется равной 0?
Решение:
Скорость движения тела есть первая производная от пути по времени:
 .
.
Полагая  , получим:
, получим:
 ,
,  ,
,  ,
,  .
.
Таким образом, скорость тела равна 0 в конце 2 и 4 секунды.
Логарифмическое дифференцирование
Логарифмической производной функции  называется производная от логарифма этой функции, т.е.
называется производная от логарифма этой функции, т.е.
 .
.
Последовательное применение логарифмирования и дифференцирования функций называют логарифмическим дифференцированием.
Пример. Найти производную функции 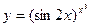 .
.
Решение:
Логарифмируя данную функцию, получаем:
 ,
,
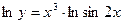 .
.
Дифференцируем обе части равенства по х:
 .
.
Отсюда  .
.
Далее  .
.
Окончательно имеем:
 .
.
Ответ:  .
.
Производная второго порядка
Производной второго порядка или второй производной называется производная от ее первой производной, т.е.  .
.
Обозначается вторая производная одним из следующих символов:  ,
,  ,
,  .
.
Пример. Найти производную второго порядка функции 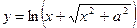 .
.
Решение:
Имеем:


Ответ: 
Дифференциал функции
Дифференциалом первого порядка функции  называется главная часть ее приращения, линейно зависящая от приращения
называется главная часть ее приращения, линейно зависящая от приращения  независимой переменной х.
независимой переменной х.
Дифференциал  функции равен произведению ее производной на дифференциал независимой переменной:
функции равен произведению ее производной на дифференциал независимой переменной:
 .
.
Пример. Найти дифференциал функции  .
.
Решение:
Находим производную данной функции:
 ,
,
 .
.
Тогда  .
.
Ответ:  .
.
Задание 3.
3.1 Найти первую производную функции:
1.




