I. Теоретический
При этом подходе математическая модель строится на основании общих законов, которыми описываются процессы в звене. Эти законы записываются с помощью системы уравнений, связывающей входные переменные, а именно управляющие и возмущающие воздействия, с выходными. Обычно это уравнения баланса массы, энергии, количества движения.
В таком варианте математическая модель получается в виде системы неоднородных нелинейных дифференциальных уравнений, не имеющей общего решения. При этом исходная математическая модель очень сложна для анализа, т.к. существуют только частные решения, и провести обобщение практически невозможно.
Иногда задачу интегрирования нелинейных уравнений удаётся свести к более простой задаче: решение линейных дифференциальных уравнений. Достаточным условием для проведения линеаризации является отсутствие неразрывных, неоднозначных функций.
Линеаризация основана на положении, что непрерывная и имеющая все производные в окрестности некоторой точки функция может быть разложена в ряд Тейлора по степеням малых отклонений элемента:
Если отклонение аргумента DU мало, то можно ограничится первыми линейными членами разложения и рассматривать вместо нелинейной функции x=f(u) линейную. Опуская символ приращения D, получим:
, где
k – коэффициент усиления звена.
В результате линеаризации получим линеаризованную математическую модель, которую обычно называют линейной математической моделью звена или системы.
В зависимости от необходимой точности можно брать различные DU, но на практике встречаются случаи, когда линеаризацию провести нельзя. Обычно это связанно с наличием в системе элементов с зонами нечувствительности, насыщения, ограничениями по положению и скорости, а так же релейных элементов. В этих случаях используют нелинейную модель, а при анализе и синтезе специальные методы.
II. Эмпирический
При построении эмпирической модели не обязательно знать природу процессов, протекающих в звене, достаточно иметь сведения об их внешних проявлениях. Достаточно исследовать реакции выходных переменных на известные входные воздействия. В результате выбирается общий вид функциональной зависимости между входным и выходным воздействием, затем определяются численные коэффициенты или параметры модели.
Ограничения: решение задачи основано на конкретном эксперименте, что делает невозможным применение к другим системам.
Понятие пространства состояний
СУ принято описывать с помощью переменных состояния, которые полностью определяют состояние системы в каждый момент времени. Переменные состояния можно рассматривать как координаты, отложенные на соответствующие оси. Тогда каждому состоянию системы будет соответствовать вполне определенная точка в пространстве состояний.
Размерность пространства состояний равна порядку системы дифференциальных уравнений, описывающих её поведение. Координатами пространства состояний являются переменные xi системы уравнений, записанные в нормальной форме Коши.
Рассмотрим линейную, детерминированную, стационарную модель, которая описывается уравнениями:
В терминах пространства состояния здесь:
x – это вектор столбец координат состояния размерностью nх1,
U – вектор столбец управляющего воздействия размерностью mх1,
y – вектор столбец измерения размерностью rх1,
A – матрица коэффициентов координат состояния размерностью nхn,
B – матрица коэффициентов управляющего воздействия размерностью nхm,
C - матрица коэффициентов измеряемых переменных размерностью rхn.
Рассмотрим нелинейную, детерминированную, нестационарную модель:
где F, G – нелинейные векторы функций, компонентами которых являются правые части исходной системы дифференциальных уравнений.
Модель в пространстве состояний связана с записью дифференциальных уравнений в стандартной форме Коши (в виде системы уравнений первого порядка):
Здесь 
– вектор переменных состояния размера 
, 
– вектор входных сигналов (вектор управления) размера 
и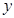 
– вектор выходных сигналов размера 
. Кроме того, 
и 
– постоянные матрицы. Согласно правилам матричных вычислений, матрица 
должна быть квадратной размера 
, матрица 
имеет размер 
, матрица 
– 
и матрица – 
. Для систем с одним входом и одним выходом[1] матрица – скалярная величина.
Это означает, что матрицы модели имеют вид
, 
, 
, 
.
Модель в пространстве состояний можно построить не для всех передаточных функций, а только для правильных, у которых степень числителя не выше, чем степень знаменателя. Например, передаточная функция
– неправильная, она не может быть преобразована в модель в пространстве состояний.
Используют также понятие строго правильной функции, у которой степень числителя меньше, чем степень знаменателя. Если построить модель в пространстве состояний для такой функции, матрица будет равна нулю, то есть, прямая передача с входа на выход отсутствует (при скачкообразном изменении входа сигнал на выходе будет непрерывным).