Лекция № 7
Линейные дифференциальные уравнения. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Дифференциальное уравнение первого порядка называется линейным, если оно содержит искомую функцию y и её производную y, в первой степени и не содержит их произведений.
Такие уравнения имеют вид:
y,+P(x)y=Q(x).
Если Q(x)=0, то уравнение y,+P(x)y=0 называется линейным уравнением без правой части (однородным).
Для решения линейных уравнений пользуются подстановкой: y=uv, y,=u,v+v,u, где u и v – некоторые функции от х.
Рассмотрим решение подобных уравнений на конкретных примерах.
Решить уравнение 
Решение. Перепишем уравнение так:

Получено линейное уравнение.
Полагаем y=uv, тогда y,= u,v+v,u.
Подставляя значения y, и y в данное уравнение, получим:

Выносим во втором и третьем слагаемом u за скобки:

Выберем v так, чтобы выражение в скобках обратилось в нуль. Это возможно, так как сомножитель v в равенстве y=uv берётся произвольно:

Разделим переменные, тогда:

Интегрируем:
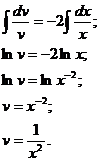
Теперь уравнение  примет вид:
примет вид:

интегрируем:

Теперь найдём искомую функцию, помня, что y=uv.

Из рассмотренного примера легко установить алгоритм решения линейного дифференциального уравнения первого порядка.
1 Приводят уравнение к виду 
2 Используя подстановку y=uv, находят y,= u,v+v,u и подставляют эти выражения в уравнение.
3 Группируют члены уравнения, выносят одну из функций u или v за скобки. Находят вторую функцию, приравняв выражение в скобках нулю и решив полученное уравнение.
4 Подставляют найденную функцию в оставшееся выражение и находят вторую функцию.
5 Записывают общее решение, подставив выражения для найденных функций u и v в равенство y=uv.
Решить уравнение 
Решение. Уравнение линейное, без правой части, так как F(x)=0. Имеем:

или, разделяя переменные, получим:

Интегрируем:

Задания для коллективного решения
Решить уравнения:


Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общий вид указанных уравнений следующий:

где p и q – постоянные коэффициенты.
Алгоритм решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами представлен в таблице № 2.
Таблица № 2. Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
| Дифференциальное уравнение |

| ||
| Характеристическое уравнение |

| ||
| Дискриминант | D>0 | D=0 | D<0 |
| Корни характеристического уравнения |

|

|

|
| Множества решений |

|

|
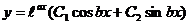
|
Рассмотрим решение подобных уравнений на конкретных примерах.
Решить уравнение 
Решение. Составляем характеристическое уравнение:

и находим его корни:
k1 = -4, k2 = 1.
Общее решение запишется так:

Решить уравнение 
Решение. Составляем характеристическое уравнение:
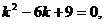
корни которого
к1=к2=к=3.
Общее решение запишется так:

Решить уравнение 
Решение. Составляем характеристическое уравнение:

корни этого уравнения


то есть корни мнимые, а = -2, b = 3.
Общее решение будет:

Задания для коллективного решения:
1 Найдите общее решение уравнений:
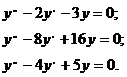
2 Найдите частное решение уравнения:
 если x=0, y(0)=2, y,(0)=3.
если x=0, y(0)=2, y,(0)=3.
Контрольные вопросы
1 Какое уравнение называется дифференциальным?
2 Назовите виды дифференциальных уравнений.
3 Рассказать алгоритмы решения всех названных в теоретической части работы уравнений.