Пусть 
произвольное множество разрешимых грамматик, тогда задача восстановления грамматики (при информативном представлении) разрешима для любой грамматики из множества , G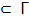 
.(индукцией)
Теорема о неразрешимости для текстуального представления грамматик
( алгоритм восстановления грамматик перечислением):
Пусть произвольное множество грамматик, содержащее все грамматики, которые порождают конечные я зыки + одна грамматика порождает бесконечный язык, тогда при текстуальном представлении задача восстановления грамматики неразрешима для произвольной грамматики из этого мн-ва.
Приведенные теоремы важны по следующим причинам:
1.они указывают ограничения на решение задачи распознавания лингвистических образов.
2.они указывают возможный способ решения задачи распознавания линг.образов, а именно: перечисление грамматик в определенном порядке.
Если находится несколько грамматик, совместных с такой последовательностью, то размер подпоследовательности увеличивается и происходит дальнейший отсев грамматик. При таком переборе истинная грамматика находится гарантированно.
Существуем множество видов перебора грамматик. Одним из них является оккамовское перечисление, при котором грамматики рассматриваются в порядке увеличения сложности.
Вывод цепочечных грамматик:
К сожалению, ни одна из известных схем не в состоянии решить эту задачу в общем виде, представленном на рис. Вместо этого предлагаются многочисленные алгоритмы для вывода ограниченных грамматик.
Алгоритм, рассматриваемый далее, является во многих отношениях типичным отражением результатов, полученных в данной области. Этот алгоритм, являющийся модификацией процедуры, разработанной Фельдманом, для заданного множества терминальных цепочек выводит автоматную грамматику.
Алгоритмы лингвистического подхода применяются в области распознавания изображений, характеризующихся хорошо различимыми формами, в частности символов, хромосом, фотоснимков столкновений частиц.
Алгоритм Фельдмана.
1. Постановка задачи:
Дано: множество выборочных цепочек {xi}.
Требуется: подвергнуть {xi} обработке с помощью адаптивного (Адаптивный алгоритм — алгоритм, который пытается выдать лучшие результаты путём постоянной подстройки под входные данные). обучающегося алгоритма, на выходе которого воспроизводится грамматика G, согласованная с данными цепочками.
Иными словами, множество цепочек {xi} является подмножеством языка L(G), порождаемого грамматикой G.
2. Суть метода:
§ сначала построить нерекурсивную грамматику, порождающую в точности заданные цепочки,
§ затем, сращивая нетерминальные элементы, получить более простую рекурсивную грамматику, порождающую бесконечное число цепочек.
3. Алгоритм + пример, чтобы понятнее было.
Сам алгоритм:
Алгоритм можно разделить на три части.
Первая часть формирует нерекурсивную грамматику.
Вторая часть преобразует её в рекурсивную грамматику.
Затем, в третьей части, происходит упрощение этой грамматики.
Рассмотрим выборочное множество терминальных цепочек 
. Требуется получить автоматную грамматику, способную порождать эти цепочки. Алгоритм построения грамматики состоит из следующих этапов.
Часть 1.
Строится нерекурсивная грамматика, порождающая в точности заданное множество выборочных цепочек. Выборочные цепочки обрабатываются в порядке уменьшения длины.
Правила подстановки строятся и прибавляются к грамматике по мере того, как они становятся нужны для построения соответствующей цепочки из выборки. Заключительное правило подстановки, используемое для порождения самой длинной выборочной цепочки, называется остаточным правилом, а длина его правой части равна 2. Остаточное правило длины 
имеет вид 
, где 
— нетерминальный символ, а 
—терминальные элементы.
Предполагается, что остаток каждой цепочки максимальной длины является суффиксом (хвостовым концом) некоторой более короткой цепочки. Если какой-либо остаток не отвечает этому условию, цепочка, равная остатку, добавляется к обучающей выборке.
Из последующих рассуждений будет ясно, что выбор остатка длины 2 не связан с ограничением на алгоритм. Можно выбрать и более длинный остаток, но тогда потребуется более полная обучающая выборка в связи с условием, что каждый остаток является суффиксом некоторой более короткой цепочки.
В нашем примере первой цепочкой максимальной длины в обучающей выборке является цепочка 
. Для порождения этой цепочки строятся следующие правила подстановки:
,
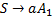
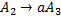
где —правило остатка.
Вторая цепочка — 
. Для порождения этой цепочки к грамматике добавляются следующие правила:
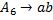
Поскольку цепочка и предыдущая цепочка имеют одинаковую длину, требуется остаточное правило длины 2. Заметим также, что работа первой части алгоритма приводит к некоторой избыточности правил подстановки. Например, вторая цепочка может быть с равным успехом получена введением следующих правил подстановки:
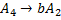
Но в первой части мы занимаемся лишь определением множества правил подстановки, которое способно в точности порождать обучающую выборку, и не касаемся вопроса избыточности. В сложных ситуациях трудно соблюдать выполнение этого условия и одновременно уменьшать число необходимых правил подстановки. Значительно проще просматривать введенные правила слева направо, чтобы определить, будут ли они порождать новую цепочку, не стремясь при этом минимизировать число правил подстановки. Об устранении избыточности речь пойдет в третьей части алгоритма.
Для порождения третьей цепочки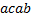 
требуется добавление к грамматике только одного правила: 
.
Для порождения четвертой цепочки 
требуется добавление к грамматике только одного правила: 
.
Для порождения пятой цепочки 
требуется добавление к грамматике только одного правила: 
.
Для порождения шестой цепочки 
требуется добавление к грамматике только одного правила: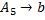 
.
Для порождения седьмой цепочки 
требуется добавление к грамматике только одного правила: 
.
Для порождения восьмой цепочки 
требуется добавление к грамматике только одного правила: 
.
Окончательно множество правил подстановки, построенных для порождения обучающей выборки, выглядит следующим образом:
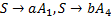
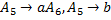
Часть 2.
В этой части, соединяя каждое правило остатка длины 2 с другим (неостаточным) правилом грамматики, получаем рекурсивную автоматную грамматику. Это происходит в результате (далее эврестическое правило) слияния каждого нетерминального элемента правила остатка с нетерминальным элементом неостаточного правила, который может порождать остаток. Так, например, если 
— остаточный нетерминал вида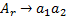 
и 
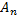— неостаточный нетерминал вида 
, где 
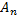, все встречающиеся заменяются на , а правило подстановки 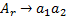отбрасывается.
Таким способом создается автоматная грамматика, способная порождать данную обучающую выборку, а также обладающая общностью, достаточной для порождения бесконечного множества других цепочек.
В рассматриваемом примере выделим остаточные правила:
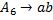
Для правила проведем поиск кандидата на слияние. Это правила вида 
. Здесь подходят следующие правила:
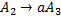
Таким образом, мы сливаем нетерминал 
с нетерминалом 
и удаляем правило (а также повторяющиеся правила):
Было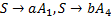
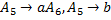
стало
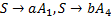
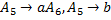
Для правила 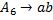проведем поиск кандидата на слияние. Это правила вида . Здесь подходят следующие правила:
Таким образом, мы сливаем нетерминал 
с нетерминалом 
и удаляем правило 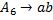(а также повторяющиеся правила):
.
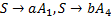
Рекурсивными правилами являются 
и 
.
Замечание. Если в результате соединения правил остатка с другими правилами грамматики остались несоединенные правила остатка (которые при длине остатка, отличной от единицы, недопустимы в автоматной грамматике), то следует разбить эти правила остатка по следующей схеме: правило остатка 
удаляется, добавляются правила
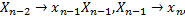
Где 
новые нетерминалы для грамматики, различные для каждого удаляемого правила остатка.
Часть 3.
Здесь грамматика, полученная во второй части, упрощается объединением эквивалентных правил подстановки.
Два правила с левыми частями 
и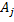 
эквивалентны, если соблюдены следующие условия. Предположим, что, начиная с , можно породить множество цепочек 
. Аналогичным образом предположим, что, начиная с 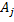, можно породить множество 
. Если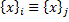 
, то два правила подстановки считаются эквивалентными, и каждый символ 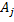может быть заменен на символ без ущерба для языка, порождаемого этой грамматикой.
Формально два правила подстановки эквивалентны, если 
, где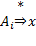 
обозначает, что цепочка 
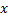порождается из нетерминала соответствующим применением правил подстановки.
В приведенном примере эквивалентны правила с левыми частями и .
Было на втором шаге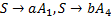
.
После слияния и получаем следующий набор правил:
,
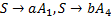
где исключены многократные повторения одного и того же правила. Дальнейшее слияние правил невозможно, поэтому алгоритм в процессе обучения строит следующую автоматную грамматику: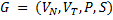 
, где:
,
,
,
.
Легко проверить, что эта грамматика может порождать обучающую выборку, использованную в процессе ее вывода.
Итак, используется восстановление грамматики индукцией, на вход алгоритма подается конечная обучающая последовательность из положительных информационных примеров, на выходе - автоматная грамматика, которая порождает выборки, включающие бесконечный язык!!! Причем пользователь в ходе алгоритма задает длину остатка, если обучающая выборка небольшая, то лучше остаток задавать меньше.
4. Алгоритм Фельдмана и автоматные грамматики:
Рассмотрим следующую автоматную грамматику 
:
,
,
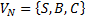Для восстановления грамматики выберем следующие цепочки 
.
Алгоритм Фельдмана при длине остатка 
конструирует следующую грамматику:
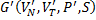
Как видно, язык грамматики таков 
. Очевидно, он не совпадает с языком исходной автоматной грамматикой (например если подставить abacc).
Для получения исходной автоматной грамматики потребуется использовать следующий набор цепочек 
. Тогда алгоритмом будет сконструирована грамматика:
.
Легко убедиться, что данная грамматика 
является эквивалентной исходной грамматике 
, то есть порождает такой же язык. Аналогичного вывода можно достичь, если использовать длины остатка 
.
Таким образом, на результат восстановления грамматики влияет размер выборки и длина остатка
5. Алгоритм Фельдмана и контекстно-свободные грамматики:
Модификация алгоритма Фельдмана для конструирования контекстно-свободных грамматик может работать следующим образом.
Первоначально алгоритм выделяет из цепочек выборки фрагменты, которые могли быть образованы правилами КС-грамматик. Такие фрагменты обычно содержатся во многих цепочках и содержат более чем два символа.
На основе выделенных фрагментов создаются правила КС-грамматики, которые их порождают. Правила имеют вид 
где 
; их множество 
. В цепочках выборки мы заменяем выбранные фрагменты некоторыми неиспользуемыми терминалами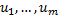 
.
Для модифицированных цепочек по алгоритму Фельдмана строится автоматная грамматика (алгоритм теперь применяется на модифицированных «автоматных» цепочках, что и позволяет получить эффективную грамматику). В результате мы получаем автоматную грамматику с набором «контекстных» правил.
Остается:
§ заменить введенные терминалы 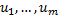на соответствующие нетерминалы 
из правил ;
§ каждое конечное правило из связать с построенной грамматикой переходом на некоторые терминалы или нетерминалы.
Пример
Рассмотрим работу модифицированного алгоритма на примере. Пусть выборка содержит цепочки 
.
Заметим здесь конструкцию 
, которая может быть построена КС-грамматикой с помощью правила из 
. Вместо во множестве цепочек будем использовать терминал 
.
Модифицируем исходное множество цепочек: 
. Применяем для него оригинальный алгоритм Фельдмана.
Получаем грамматику 
, где
После этого введем конструкции правил КС-грамматики 
:
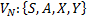
Здесь правило 
является конечным, оно должно быть связано с построенной грамматикой посредством введения нового нетерминала 
.
В результате грамматика является контекстно-свободной.
ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ
Постановка задачи:
Предположим, у нас имеются два класса образов w1 и w2 и пусть образы образы этих классов могут быть построены из признаков, принадлежащих некоторому конечному множеству. Назовем эти признаки терминалами и обозначим множество терминалов символом Vт.
В синтаксическом распознавании образов терминалы называются также непроизводными символами (элементами). Каждый образ может рассматриваться как цепочка или предложение, поскольку он составлен из терминалов множества VT. Допустим, что существует грамматика G, такая, что порождаемый ею язык состоит из предложений (образов), принадлежащих исключительно одному из классов, скажем w1. Очевидно, что эта грамматика может быть использована в целях классификации образов, так как заданный образ неизвестной природы может быть отнесен к w1 если он является предложением языка L(G).В противном случае образ приписывается классу w2.
Например, бесконтекстная грамматика G = (Vn, Vт, P, S) при Vn= {S}, Vt= {a, b) и
множестве правил подстановки Р= {S->aaSb, S->aab} обладает способностью порождать лишь предложения, содержащие вдвое больше символов а, чем Ь. Если мы сформулируем гипотетическую задачу разбиения образов на два класса, причем объекты класса w1 — это цепочки вида aab, aaaabb и т. д., а объекты класса w2 содержат одинаковое число символов а и Ь (т. е. ab, aabb и т. д.), то очевидно, что классификация заданной цепочки производится простым определением того, может ли данная цепочка порождаться грамматикой G, рассмотренной выше. Если может, то объект принадлежит w1, если нет — он автоматически приписывается классу w2. Процедура, используемая для определения, является или не является цепочка предложением, грамматически правильным для данного языка, называется грамматическим разбором.
Постановка задачи по Фельдману можно сформулировать как:
· Дано: множество выборочных цепочек 
.
· Требуется: подвергнуть 
обработке с помощью адаптивного обучающегося алгоритма, на выходе которого воспроизводится грамматика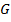 
, согласованная с данными цепочками.
· Т.е. множество цепочек является подмножеством языка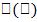 
, порождаемого грамматикой 
.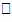