Понятие линейного векторного пространства. Примеры линейного векторного пространства.
Векторное (линейное) пространство — это математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр.
Примеры линейных пространств
1. Обозначим 
— множество, содержащее один нулевой вектор, с операциями 
и 
. Для указанных операций аксиомы 1-8 выполняются. Следовательно, множество является линейным пространством над любым числовым полем. Это линейное пространство называется нулевым.
2. Обозначим 
— множества векторов (направленных отрезков) на прямой, на плоскости, в пространстве соответственно с обычными операциями сложения векторов и умножения векторов на число. Выполнение аксиом 1-8 линейного пространства следует из курса элементарной геометрии. Следовательно, множества являются вещественными линейными пространствами. Вместо свободных векторов можно рассмотреть соответствующие множества радиус-векторов. Например, множество векторов на плоскости, имеющих общее начало, т.е. отложенных от одной фиксированной точки плоскости, является вещественным линейным пространством. Множество радиус-векторов единичной длины не образует линейное пространство, так как для любого из этих векторов сумма 
не принадлежит рассматриваемому множеству.
3. Обозначим 
— множество матриц-столбцов размеров 
с операциями сложения матриц и умножения матриц на число. Аксиомы 1-8 линейного пространства для этого множества выполняются. Нулевым вектором в этом множестве служит нулевой столбец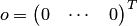 
. Следовательно, множество является вещественным линейным пространством. Аналогично, множество 
столбцов размеров с комплексными элементами является комплексным линейным пространством. Множество матриц-столбцов с неотрицательными действительными элементами, напротив, не является линейным пространством, так как не содержит противоположных векторов.
4. Обозначим 
— множество решений однородной системы 
линейных алгебраических уравнений с и неизвестными (где 
— действительная матрица системы), рассматриваемое как множество столбцов размеров с операциями сложения матриц и умножения матриц на число. Заметим, что эти операции действительно определены на множестве . Из свойства 1 решений однородной системы (см. разд. 5.5) следует, что сумма двух решений однородной системы и произведение ее решения на число также являются решениями однородной системы, т.е. принадлежат множеству . Аксиомы линейного пространства для столбцов выполняются (см. пункт 3 в примерах линейных пространств). Поэтому множество решений однородной системы является вещественным линейным пространством.
Множество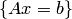 
решений неоднородной системы 
, напротив, не является линейным пространством, хотя бы потому, что не содержит нулевого элемента (
не является решением неоднородной системы).
5. Обозначим 
— множество матриц размеров 
с операциями сложения матриц и умножения матриц на число. Аксиомы 1-8 линейного пространства для этого множества выполняются. Нулевым вектором является нулевая матрица 
соответствующих размеров. Следовательно, множество является линейным пространством.
6. Обозначим 
— множество многочленов одной переменной с комплексными коэффициентами. Операции сложения много членов и умножения многочлена на число, рассматриваемое как многочлен нулевой степени, определены и удовлетворяют аксиомам 1-8 (в частности, нулевым вектором является многочлен, тождественно равный нулю). Поэтому множество является линейным пространством над полем комплексных чисел. Множество 
многочленов с действительными коэффициентами также является линейным пространством (но, разумеется, над полем действительных чисел). Множество 
многочленов степени не выше, чем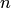 
, с действительными коэффициентами также является вещественным линейным пространством. Заметим, что операция сложения много членов определена на этом множестве, так как степень суммы многочленов не превышает степеней слагаемых.
Множество многочленов степени 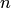не является линейным пространством, так как сумма таких многочленов может оказаться многочленом меньшей степени, не принадлежащим рассматриваемому множеству. Множество всех многочленов степени не выше, чем л, с положительными коэффициентами также не является линейным пространством, поскольку при умножении такого многочлена на отрицательное число получим многочлен, не принадлежащий этому множеству.
7. Обозначим 
— множество действительных функций, определенных и непрерывных на 
. Сумма 
функций 
и произведение 
функции 
на действительное число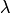 
определяются равенствами:
для всех 
1. 
(коммутативность сложения);
2. (ассоциативность сложения);
3. существует такой элемент 
, называемый нулевым вектором, что 
;
4. для каждого вектора 
существует такой вектор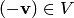 
, называемый противоположным вектору , что 
;
2) понятие системы линейных уравнений и ее решения
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
Элементарными преобразованиями строк называют:
· перестановка местами любых двух строк матрицы;
· умножение любой строки матрицы на константу  ,  ;
· прибавление к любой строке матрицы другой строки.
3) Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы.
4) однородная система уравнений и свойства ее решений
1. Если столбцы  — решения однородной системы уравнений, то любая их линейная комбинация  также является решением однородной системы.
В самом деле, из равенств  следует, что
т.е. линейная комбинация решений является решением однородной системы.
2. Если ранг матрицы однородной системы равен  , то система имеет  линейно независимых решений.
Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений  , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):
В однородной системе линейных уравнений ответ равен нулю, а не в однородных нет.
5) Два вектора плоскости линейно зависимы тогда и только тогда, когда они коллинеарны.
|
Система элементов линейного пространства {a1,…,an} называется линейно зависимой, если найдутся коэффициенты λ1,…,λn не все равные нулю, линейная комбинация с которыми равна нулю, т.е. 
Определение 3. Система элементов линейного пространства {a1,…,an} называется линейно
независимой, если ее линейная комбинация равна нулю только с нулевыми коэффициентами: 
Имеют место несколько простых утверждений.
Теорема 1 (необходимое и достаточное условие линейной независимости). a1,…,an – линейно зависима 
когда хотя бы один из элементов является линейной комбинацией остальных.
{1.(необходимость: { ak } – л.з.): 
. Пусть, для определенности, 
а1 – линейная комбинация остальных.
2.(достаточность: am – л.к.): 
}
6) свойство линейно зависимые и линейно независимые системы
линейно зависимо
· 
линейно независимо 
линейно независимо для всех 
· линейно зависимо линейно зависимо для всех 
7) Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.
Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.
8) Рангом системы векторов называется максимальное число линейно независимых векторов системы.
Свойство ранга.
1 ранг матрицы, полученной транспонированием, равен рангу исходной матрицы.
2 Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку или столбец.
Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.
9) Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
10) Матрицей размером называется совокупность 
чисел, расположенных в виде прямоугольной таблицы из 
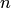строк и столбцов:
1. 
(коммутативность сложения);
2. 
(ассоциативность сложения);
3. существует нулевая матрица (тех же размеров, что и ): 
4. существует матрица 
, противоположная матрице 
;
5. 
;
6. 
;
7. 
;
8. 
.
Матрици можно складывать,вычитать, умножать матрицу на число и на другую матрицу.
11) Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
Свойства
· 
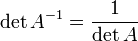, где 
обозначает определитель.
· 
для любых двух обратимых матриц 
и 
.
· 
где 
обозначает транспонированную матрицу.
· 
для любого коэффициента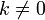 
.
12) определитель
Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равны)
13)
Минором 
к элементу 
определителя 
-го порядка называется определитель 
-го порядка, полученный из исходного вычеркиванием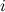 
-той строки и 
-того столбца.
Пример
Задание. Найти минор 
к элементу 
определителя 
.
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
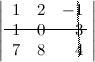
тогда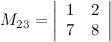 
Ответ.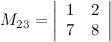
Алгебраическим дополнением 
к элементу определителя -го порядка называется число 
Пример
Задание. Найти алгебраическое дополнение 
к элементу определителя .
Решение.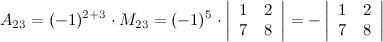 
Ответ. 
Теорема лапласа
Пусть 
- определитель -го порядка. Выберем в нем произвольные 
строк (или столбцов), причем 
. Тогда сумма произведений всех миноров -го порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.