Алгебра и начала математического анализа; геометрия
Методические указания
По выполнению контрольной работы
Для студентов 2 курса заочного отделения
(3 семестр)
Заречный 2016
 |
Голянова О.Н.
Математика: алгебра и начала математического анализа; геометрия. Методические указания по выполнению контрольной работы для студентов 2 курса заочного отделения. 2016. – стр.28
Методические указания содержат варианты заданий для контрольной работы по дисциплине «Математика: алгебра и начала математического анализа; геометрия», необходимые теоретические сведения, примеры решения типовых задач. Методические указания предназначены для студентов 2 курса заочной формы обучения по специальности 38.02.04 «Коммерция по отраслям» и составлена в соответствии с рабочей программой дисциплины.
Методические указания рассмотрены на заседании цикловой методической комиссии общеобразовательных, естественнонаучных и ОГСЭ дисциплин Зареченского технологического института – филиала Пензенского государственного технологического университета.
Протокол №1 от 31.08.2016 г.
Методические указания одобрены и рекомендованы методическим советом Зареченского технологического института – филиала Пензенского государственного технологического университета для использования в учебном процессе.
Протокол №1 от 31.08.2016 г.
Содержание
Раздел 3. Геометрия.. 4
Тема 3.1. Прямые и плоскости в пространстве. 4
Тема 3.2. Многогранники. 10
Тема 3.3. Тела и поверхности вращения. 14
Тема 3.4. Координаты и векторы в пространстве. 16
Задания для контрольной работы.. 18
Раздел 3. Геометрия
Тема 3.1. Прямые и плоскости в пространстве
Плоскость в пространстве однозначно задаётся:
тремя точками, не лежащими прямой и точкой, не лежащей
на одной прямой на этой прямой
двумя пересекающимися прямыми двумя параллельными прямыми
| Прямые в пространстве | ||
| 
| 
|
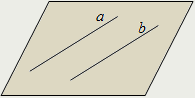
| Две прямые в пространстве пересекаются, если они имеют лишь одну общую точку: a∩b = C. | Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются: a || b. | Две прямые в пространстве называются скрещивающимися, если не существует плоскости, которой эти прямые принадлежат: a · b. |
| Признак параллельности прямых: Две прямые, параллельные третьей прямой, параллельны между собой: a || c, b || c ⇒ a || b. |
| Прямая и плоскость в пространстве | ||
| 
| 
|
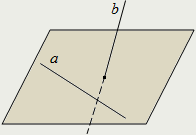
| Если каждая точка прямой принадлежит плоскости, то говорят, что и прямая принадлежит плоскости: а ∈ α. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости: А ∈ α, В ∈ α ⇒ а ∈ α. | Говорят, что прямая и плоскость пересекаются, если они имеют одну единственную общую точку: a ∩ α = А. Точку А называют точкой пересечения прямой и плоскости или следом прямой а на плоскости α. | Прямая и плоскость называются параллельными, если они не имеют общих точек: а || α. Плоскость и не лежащая на ней прямая либо пересекаются (в одной точке), либо не пересекаются (параллельны). |
| Признак параллельности прямой и плоскости: Прямая, не лежащая в плоскости, параллельна этой плоскости тогда и только тогда, когда она параллельна некоторой прямой в этой плоскости: а ∉ α, ∃ b ∈ α, а || b ⇔ а || α. | |
| Признак параллельности прямых: Если прямая b параллельна плоскости α, а плоскость β проходит через b и пересекает плоскость α по прямой а, то прямые а и b параллельны: b || α, α ∩ β = a ⇒ а || b. | |
| Признак параллельности прямых: Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна и линии пересечения этих плоскостей: a || α, a || β, α ∩ β = b ⇒ а || b. | |
| Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения этой прямой и плоскости. Через любую точку пространства можно провести прямую, перпендикулярную данной плоскости, и притом только одну. Признак перпендикулярности прямой и плоскости: Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости: b ∈ α, c ∈ α, a ⊥ b, a ⊥ c ⇒ a ⊥ α. |
| Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой прямой: a ⊥ α, а || b ⇒ b ⊥ α. Прямые, перпендикулярные одной плоскости, – параллельны: a ⊥ α, b ⊥ α ⇒ а || b. | |||||
| Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок, которые соединяет эту точку с точкой плоскости (основанием перпендикуляра) и лежит на прямой, которая перпендикулярна плоскости. Длину перпендикуляра, проведённого из данной точки к данной плоскости, считают расстоянием между этими точкой и плоскостью. Наклонной, проведённой из данной точки к плоскости, называется любой отрезок, который соединяет эту точку с точкой плоскости (основанием перпендикуляра) и не является перпендикуляром, проведённым к этой плоскости. | |||||
Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых к плоскости из одной точки, называется проекцией (ортогональной проекцией) этой наклонной на плоскость.
АВ – перпендикуляр, проведённый из точки А к плоскости α;
АС – наклонная, проведённая из точки А к плоскости α;
В – основание перпендикуляра АВ;
С – основание наклонной АС;
ВС – проекция наклонной АС на плоскость α.
Свойства перпендикуляра и наклонной:
| ||||||
| Углом между наклонной и плоскость называется величина угла между наклонной и её ортогональной проекцией на эту плоскость: ∠АСВ – угол между наклонной АС и плоскостью α. Угол между наклонной и её ортогональной проекцией на плоскость меньше угла между этой наклонной и любой другой прямой, проходящей в этой плоскости через основание наклонной: ∠АСВ < ∠АСD. | |||||
| Теорема про три перпендикуляра: Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной. И наоборот: если прямая, проведённая на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и проекции этой наклонной: АВ ⊥ α, а ∈ α: а ⊥ ВС ⇔ а ⊥ АС. | |||||
| Расстоянием от прямой до параллельной ей плоскости называется расстояние от любой точки этой прямой до плоскости: АВ – расстояние от прямой а до плоскости α. Отрезок АВ – общий перпендикуляр прямой а и плоскости α. | |||||
| Общим перпендикуляром двух скрещивающихся прямых (a и b) называется отрезок (АВ) с концами на этих прямых, являющийся перпендикуляром к каждой из них. Две скрещивающиеся прямые всегда имеют общий перпендикуляр, и притом только один. Длина общего перпендикуляра двух скрещивающихся прямых считается расстоянием между ними: АВ – расстояние между скрещивающимися a и b. | |||||
| Плоскости в пространстве | ||||||
Говорят, что две плоскости пересекаются, если в одной из них существуют точки как принадлежащие другой плоскости, так и не принадлежащие ей.
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку:
α ∩ β = с.
|
Говорят, что две плоскости совпадают, если каждая точка одной плоскости является точкой другой, и наоборот:
α ∩ β = α
или
α ∩ β = β.
|
Две плоскости называются параллельными, если они не имеют общих точек:
α || β ⇔ α ∩ β = ∅.
Через точку вне плоскости можно провести плоскость параллельную данной и притом только одну.
| ||||
Признак параллельности плоскостей:
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны:
a ∈ α, b ∈ α, a1 ∈ β, b1 ∈ β, a ∩ b
⇓
 α || β.
| ||||||
| Расстоянием между двумя параллельными плоскостями называется расстояние от любой точки одной плоскости до другой плоскости. Длина некоторого отрезка выражает расстояние между двумя параллельными плоскостями, если этот отрезок является общим перпендикуляром этих плоскостей: А ∈ α, В ∈ β, АВ ⊥ α, АВ ⊥ β ⇓ АВ – расстояние от α до β. | |||||
| Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой. Полуплоскости, о которых шла речь, называются гранями двугранного угла, а прямая – ребром двугранного угла: α и β – грани, KL – ребро двугранного угла. | |||||
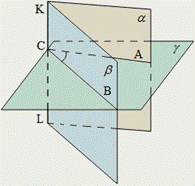
| Плоскость γ, перпендикулярная ребру двугранного угла KL, пересекает его грани α и β по двум полупрямым: СА и СВ. Угол АВС, образованный этими полупрямыми, называется линейным углом двугранного угла. Все линейные углы данного двугранного угла совмещаются параллельным переносом и равны. Мера линейного угла служит мерой и двугранного угла, которому этот линейный угол соответствует. Линейные углы, соответствующие равным двугранным углам, равны. И наоборот: равным линейным углам соответствуют равные двугранные углы. | |||||
| Углом между двумя пересекающимися плоскостями называется наименьшая из мер двухгранных углов, образованных этими плоскостями. Две плоскости называются перпендикулярными (α⊥β), если угол между ними равен 90°. Угол между параллельными плоскостями считается равным 0°. Если φ – величина угла между некоторыми двумя плоскостями, то 0º ≤ φ ≤ 90º. Признак перпендикулярности плоскостей: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны: b ∈ β, b ⊥ α ⇒ α ⊥ β. Прямая, проведённая в одной из двух перпендикулярных плоскостей перпендикулярно линии их пересечения, перпендикулярна другой плоскости: b ∈ β, α ⊥ β b ⊥ с, с = α ∩ β ⇒ b ⊥ α. | |||||
| Некоторые свойства прямых и плоскостей | ||||||
| Отрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны: α || β и a || b || c ⇒ A1A2 = B1B2 = C1C2 . | |||||
| Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость; более того, эта прямая образует с параллельными плоскостями равные углы: α || β ⇒ ∠CBE = ∠CAD. | |||||
| Прямые, полученные при пересечении двух параллельных плоскостей третьей плоскостью, параллельны между собой: α || β, α ∩ γ = а, β ∩ γ = b ⇒ a || b. Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости: c ⊥ α, α || β ⇒ c ⊥ β. Две плоскости, перпендикулярные одной и той же прямой, параллельны: α ⊥ c, β ⊥ c ⇒ α || β. Плоскость, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости: γ ⊥ α, α || β ⇒ γ ⊥ β. | |||||
Тема 3.2. Многогранники
Основные понятия
Некоторые пространственные фигуры, изучаемые в стереометрии, называют телами или геометрическими телами. Наглядно тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
Многогранником называется геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Выпуклым называется многогранник, если он расположен по одну сторону плоскости, проведённой через любой многоугольник, образующий поверхность данного многогранника.
Многоугольники, составляющие поверхность многогранника, называются его гранями; стороны многоугольников – рёбрами; вершины – вершинами многогранника:
ABC, DEF, ABED, BCFE, ACFD – грани;
AB, BC, AC, DE, EF, DF, AD, BE, CF – рёбра;
A, B, C, D, E, F – вершины многогранника ABCDEF.
Теорема Эйлера для многогранников:
Если V — число вершин выпуклого многогранника, R — число его ребер и G — число граней, то верно равенство:
V – R + G = 2.
Призма
Призмой называется многогранник, состоящий из двух плоских многоугольников, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники, о которых шла речь, называются основаниями призмы, а отрезки, соединяющие их соответствующие вершины – боковыми рёбрами призмы.
Основания призмы равны и лежат в параллельных плоскостях.
Боковые рёбра призмы равны и параллельны.
Поверхность призмы состоит из двух оснований и боковой поверхности.
Боковая поверхность любой призмы состоит из параллелограммов, у каждого из которых две стороны являются соответствующими сторонами оснований, а две другие – соседними боковыми рёбрами.
Высотой призмы называется любой из перпендикуляров, проведённых из точки одного основания к плоскости другого основания призмы.
Призма называется п -угольной, если её основание – п -угольник.
АВСA1В1С1 – треугольная призма;
ΔАВС и ΔA1В1С1 – основания;
АA1, ВВ1, СС1 – боковые рёбра;
АA1В1В, АA1С1С, ВВ1С1С – боковые грани;
A1О – высота призмы;
α – угол наклона бокового ребра к основанию призмы.
Призма называется прямой, если её рёбра перпендикулярны плоскостям оснований. В противном случае призма называется наклонной.
Боковые грани прямой призмы – прямоугольники.
Боковое ребро прямой призмы является её высотой.
Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы:
Sб = Pосн·АА1.
Прямая призма называется правильной, если её основания являются правильными многоугольниками.
Параллелепипед
Призма, в основании которой лежит параллелограмм, называется параллелепипедом.
У параллелепипеда все грани – параллелограммы.
Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
У параллелепипеда противолежащие грани параллельны и равны.
Диагональю параллелепипеда, как и многогранника вообще, называется отрезок, соединяющий вершины параллелепипеда, не лежащие в одной его грани.
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Точка пересечения диагоналей параллелепипеда является его центром симметрии.
Прямоугольным параллелепипедом называется такой прямой параллелепипед, в основании которого лежит прямоугольник.
Все грани прямоугольного параллелепипеда являются прямоугольниками.
Длины рёбер прямоугольного параллелепипеда, выходящих из одной вершины, называются его измерениями или линейными размерами.
У прямоугольного параллелепипеда три измерения.
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений:
d ² = a ² + b ² + c ².
В прямоугольном параллелепипеде верно:
· для площади полной поверхности:
Sп = 2·(ab+bc+ac);
· для объёма:
V = abc.
Куб
Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.
Диагональ куба в квадратный корень из трёх раз больше его стороны:
В кубе верно:
- для площади полной поверхности:
Sп = 6· a ², Sп = 2· d ²,
- для объёма:
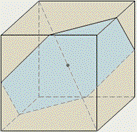Четыре сечения куба являются правильными шестиугольниками (одно из них показано на рисунке) – эти сечения проходят через центр куба перпендикулярно четырём его диагоналям.
У куба девять плоскостей симметрии:
- три из них, проходя через середины четырёх параллельных ребер куба, дают в сечениях квадраты;
- остальные шесть – это все плоскости диагональных сечений куба.
Пирамида
Пирамидой (например, SABCDE) называется многогранник, который состоит из плоского многоугольника (пятиугольник ABCDE) – основания пирамиды, точки (S), не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.
Отрезки (SA, SB, SC, SD, SE), соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Поверхность пирамиды состоит из основания (пятиугольник ABCDE) и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды:
ΔSAB, ΔSBC, ΔSCD, ΔSDE, ΔSEA – боковые грани.
Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.
Высотой пирамиды (SО) называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания.
Пирамида называется n -угольной, если ее основанием является n -угольник. Треугольная пирамида называется также тетраэдром.
α – угол наклона бокового ребра SA пирамиды к плоскости её основания;
β – угол наклона боковой грани (SED) пирамиды к плоскости её основания.
Основание высоты пирамиды является центром окружности, описанной около основания пирамиды, тогда и только тогда, когда выполняется одно из условий:
- все боковые ребра равны;
- боковые ребра образуют с плоскостью основания равные углы;
- боковые ребра образуют равные углы с высотой пирамиды.
Основание высоты пирамиды является центром окружности, вписанной в основание пирамиды, тогда и только тогда, когда выполняется одно из условий:
- боковые грани наклонены к плоскости основания под одним углом;
- высоты боковых граней равны;
- боковые грани образуют равные углы с высотой пирамиды.
Объём пирамиды равен трети произведения площади основания на высоту пирамиды:
V = 1/3·Sоснh.
Площадь полной поверхности любой пирамиды равна сумме площадей боковой поверхности и основания:
Sп = Sб + Sосн.
Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды.
Пирамида (например, SABCD) называется правильной, если ее основанием является правильный многоугольник (ABCD – квадрат), а основание высоты совпадает с центром этого многоугольника (О – центр описанной и вписанной окружностей основания).
Осью правильной пирамиды называется прямая, содержащая ее высоту.
Боковые ребра правильной пирамиды равны.
Боковые грани правильной пирамиды – равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды (SL), проведенная из ее вершины к стороне основания, называется апофемой.
Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему:
Sб = ½Pосн·SL.