Правило обучения Видроу-Хоффа
Используется для обучения нейронной сети, состоящей из распределительных нейронов и одного выходного нейрона, который имеет линейную функцию активации (рис.1):
Рис. 1.Линейная сеть.
Такая сеть называется адаптивным нейронным элементом или "ADALINE" (Adaptive Linear Element). Его предложили в 1960 г. Видроу (Widrow) и Хофф (Hoff). Выходное значение такой сети определяется, как
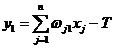. (1.2)
Правило обучения Видроу Хоффа известно под названием дельта правила (delta rule). Оно предполагает минимизацию среднеквадратичной ошибки нейронной сети, которая для L входных образов определяется следующим образом:
(1.3)
где 
— среднеквадратичная ошибка сети для k -го образа; 
и 
— соответственно выходное и эталонное значение нейронной сети для k -го образа.
Критерий (1.3) характеризуется тем, что при малых ошибках ущерб является также малой величиной, т. к. 
меньше чем величина отклонения 
. При больших ошибках ущерб возрастает, так как возрастает с ростом величины ошибки.
Среднеквадратичная ошибка нейронной сети для одного входного образа определяется, как
(1.4)
Правило обучения Видроу-Хоффа базируется на методе градиентного спуска в пространстве весовых коэффициентов и порогов нейронной сети. Согласно этому правилу, весовые коэффициенты и пороги нейронной сети необходимо изменять с течением времени по следующим выражениям:
(1.5)
(1.6)
где 
; 
— скорость или шаг обучения. Найдем производные
среднеквадратичной ошибки по настраиваемым параметрам сети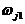 
и 
. Тогда
где xjk — j -ая компонента k -го образа.
Отсюда получаем следующие выражения для обучения нейронной сети по дельта правилу:
(1.7)
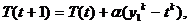(1.8)
где .
Видроу и Хофф доказали [18], что данный закон обучения всегда позволяет находить весовые коэффициенты нейронного элемента таким образом, чтобы минимизировать среднеквадратичную ошибку сети независимо от начальных значений весовых коэффициентов.
Алгоритм обучения, в основе которого лежит дельта правило состоит из следующих шагов:
1. Задается скорость обучения 
и минимальная среднеквадратичная ошибка сети 
, которой необходимо достичь в процессе обучения.
2. Случайным образом инициализируются весовые коэффициенты и порог нейронной сети.
3. Подаются входные образы на нейронную сеть и вычисляются векторы выходной активности сети.
4. Производится изменение весовых коэффициентов и порога нейронной сети согласно выражениям (1.7) и (1.8).
5. Алгоритм продолжается до тех пор, пока суммарная среднеквадратичная ошибка сети не станет меньше заданной, т. е.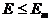 
.
В алгоритме Видроу-Хоффа существует проблема выбора значения шага обучения . Если коэффициент слишком мал, то процесс обучения является очень длительным. В случае, когда шаг обучения большой, процесс обучения может оказаться расходящимся, то есть не привести к решению задачи. Таким образом сходимость алгоритма обучения не избавляет от разумного выбора значения шага обучения.
Использование линейной нейронной сети для прогнозирования
Способность нейронных сетей после обучения к обобщению и пролонгации результатов создает потенциальные предпосылки для построения на базе их различного рода прогнозирующих систем. В данном разделе рассмотрим прогнозирование временных рядов при помощи линейных нейронных сетей. Пусть дан временной ряд 
на промежутке 
. Тогда задача прогнозирования состоит в том, чтобы найти продолжение временного ряда на неизвестном промежутке, т. е. необходимо определить 
, 
и так далее (рис. 1.2):
Совокупность известных значений временного ряда образуют обучающую выборку, размерность которой равняется m. Для прогнозирования временных рядов используется метод "скользящего окна". Он характеризуется длиной окна n, которая равняется количеству элементов ряда, одновременно подаваемых на нейронную сеть. Это определяет структуру нейронной сети, которая состоит из n распределительных нейронов и одного выходного нейрона.
Такая модель соответствует линейной авторегрессии и описывается следующим выражением:
где 
— весовые коэффициенты нейронной сети; 
— оценка значения ряда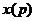 
в момент времени 
.
Рис. 1.2. Прогнозирование временного ряда.
Ошибка прогнозирования определяется, как
.
Модель линейной авторегрессии формирует значение ряда 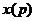, как взвешенную сумму предыдущих значений ряда. Обучающую выборку нейронной сети можно представить в виде матрицы, строки которой характеризуют векторы, подаваемые на вход сети:
.
Это эквивалентно перемещению окна по ряду с единичным шагом.
Таким образом для обучения нейронной сети прогнозированию используется выборка известных членов ряда. После обучения сеть должна прогнозировать временной ряд на упреждающий промежуток времени.
Задание.
1. Написать на любом ЯВУ программу моделирования прогнозирующей линейной ИНС. Для тестирования использовать функцию
.
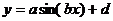Варианты заданий приведены в следующей таблице:
| № варианта | a | b | d | Кол-во входов ИНС |
| 0.1 | ||||
| 0.2 | ||||
| 0.3 | ||||
| 0.4 | ||||
| 0.5 | ||||
| 0.6 | ||||
| 0.1 | ||||
| 0.2 | ||||
| 0.3 | ||||
| 0.4 | ||||
| 0.5 |
Обучение и прогнозирование производить на 30 и 15 значениях соответственно табулируя функцию с шагом 0.1. Скорость обучения выбирается студентом самостоятельно, для чего моделирование проводится несколько раз для разных a. Результаты оцениваются по двум критериям - скорости обучения и минимальной достигнутой ошибке. Необходимо заметить, что эти критерии в общем случае являются взаимоисключающими, и оптимальные значения для каждого критерия достигаются при разных a.
2. Результаты представить в виде отчета содержащего:
1. Титульный лист,
2. Цель работы,
3. Задание,
4. Результаты обучения: таблицу со столбцами: эталонное значение, полученное значение, отклонение; график изменения ошибки в зависимости от итерации.
5. Результаты прогнозирования: таблицу со столбцами: эталонное значение, полученное значение, отклонение.
6. Выводы по лабораторной работе.
Результаты для пунктов 3 и 4 приводятся для значения a, при котором достигается минимальная ошибка. В выводах анализируются все полученные результаты.
Контрольные вопросы.
1. ИНС какой архитектуры Вы использовали в данной работе? Опишите принцип построения этой ИНС.
2. Как функционирует используема Вами ИНС?
3. Опишите (в общих чертах) алгоритм обучения Вашей ИНС.
4. Как формируется обучающая выборка для решения задачи прогнозирования?
5. Как выполняется многошаговое прогнозирование временного ряда?
6. Предложите критерий оценки качества результатов прогноза.