Условия совместности систем линейных уравнений.

Глава 2

СИСТЕМЫЛИНЕЙНЫХ УРАВНЕНИЙ

Понятие системы линейных уравнений (СЛУ).

Матричная форма записи СЛУ

Определение 2.1.1. Системой m линейных уравнений с n неизвестными будем называть систему вида:

(2.1.1)

или в сокращенной записи:

, (2.1. )

где .

Коэффициенты при неизвестных составляют прямоугольную матрицу размера , которую будем называть матрицей (основной матрицей) системы. Числа, стоящие в правых частях уравнений системы (2.1.1), образуют столбцевую матрицу размера , называемую столбцом свободных членов.

Определение 2.1.2. Матрица системы, дополненная справа столбцом свободных членов, называется расширенной матрицей системы и обозначается .

Таким образом, следующие матрицы

(2.1.2)

 

являются основной, столбцом свободных членов и расширенной матрицами системы (2.1.1) соответственно.

Определение 2.1.3. Система, у которой все свободные члены равны нулю, т. е. , называется однородной. Если хотя бы один из свободных членов отличен от нуля, т.е. , то система называется неоднородной.

Определение 2.1.4. Упорядоченный набор чисел называется решением системы (2.1.1), если при подстановке этих чисел в систему вместо соответствующих неизвестных каждое уравнение системы обращается в тождество.

Решение системы можно записывать также в виде столбцевой матрицы

(2.1.3)

которую будем называть вектор-решением данной системы.

Определение 2.1.5. Если система имеет хотя бы одно решение, то она называется совместной, в противном случае – несовместной.

Определение 2.1.6. Совместная система называется определенной, если она имеет единственное решение. Совместная система, имеющая более одного решения, называется неопределенной.

Определение 2.1.7. Решить систему означает: 1) выяснить является ли система совместной; 2) если система совместна, то определить количество решений, т.е. установить является система определенной или нет, и найти все ее решения.

Пример 2.1.1.

a) b) c)

Решая систему a) методом сложения, получим, что она имеет единственное решение и, следовательно, является определенной. Система b), состоящая из одного уравнения с двумя неизвестными, имеет бесконечно много решений , где 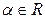, т. е. является неопределенной. Система c)не имеет ни одного решения, так как левые части уравнений совпадают, а правые различны, и поэтому никакой набор чисел не может одновременно удовлетворять обоим уравнениям; т. е. система несовместна.

Определение 2.1.8. Две системы называются эквивалентными, если они имеют одни и те же решения или обе несовместные.

Систему линейных уравнений (2.1.1) можно записать в матричной форме:

, (2.1.4)

где А и В матрицы , а – столбцевая матрица высоты , составленная из

неизвестных.

Действительно, произведение матрицы 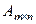на матрицу определено, и согласно правилу умножения матриц (1.2.4) имеем:

Элементами полученной столбцевой 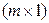-матрицы являются левые части уравнений системы (2.1.1). Воспользовавшись определением 1.1.2 о равенстве двух матриц, из (2.1.3) получаем в точности систему (2.1.1).

Существует еще одна матричная форма записи системы (2.1.1):

, (2.1. )

где под подразумеваются столбцевые матрицы (1.1.4), являющиеся столбцами матрицы A системы.

Каждой системе (2.1.1) соответствует единственная пара матриц A, B и наоборот.

 

 

Условия совместности систем линейных уравнений.

Теорема Кронекера–Капелли*

Решая вопрос о совместности системы (2.1.1), рассмотрим матрицы и из (2.1.2). Их ранги либо совпадают, либо отличаются на единицу. В самом деле, так как матрицы и отличаются друг от друга лишь входящим в столбцом свободных членов, то либо базисный минор матрицы будет являться базисным и для матрицы , либо порядок базисного минора матрицы увеличится на единицу.

Ответ на вопрос о совместности системы линейных уравнений (2.1.1) дает теорема, которая называется теоремой Кронекера–Капелли.

Теорема 2.2.1 (Кронекера–Капелли, критерий совместности системы линейных уравнений). Система неоднородных линейных уравнений (2.1.1) тогда и только тогда совместна, когда ранги ее основной и расширенной матриц совпадают.

Доказательство.

Необходимость. Пусть система (2.1.1) совместна, т. е. имеет хотя бы одно решение . Тогда этот набор должен удовлетворять каждому уравнению системы. Подставляя его в (2.1. ), имеем:

. (2.2.1)

Таким образом, столбец свободных членов В представляет собой линейную комбинацию столбцов матрицы A, и, следовательно, по теореме о базисном миноре (1.5.2), он не является базисным. Это означает, что .

Достаточность. Пусть 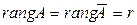. Докажем, что система совместна. Так как , то существует минор , являющийся базисным минором как матрицы , так и матрицы . На основании теоремы 1.5.2 о базисном миноре, последний столбец матрицы является линейной комбинацией r базисных столбцов. К этому равенству можно прибавить остальные (n–r) столбцов матрицы А, умноженные на нуль, т. е. получим равенство вида (2.2.1). А это и означает, что числовые коэффициенты из разложения (2.2.1) составляют решение системы (2.1.1) и, следовательно, система совместна.

Теорема 2.2.2. Совместнаясистема линейных уравнений (2.1.1) тогда и только тогда имеет единственное решение, когда , где n – количество неизвестных.

Замечание 2.2.1. Если в системе (2.1.1) количество уравнений совпадает с количеством неизвестных (m=n), то согласно замечанию 1.5.2.c, для того чтобы система имела единственное решение, необходимо и достаточно, чтобы .

Теорема 2.2.3. Совместнаясистема линейных уравнений (2.1.1) тогда и только тогда имеет бесконечное множество решений, когда ранг матрицы системы меньше числа неизвестных, т.е. .

Пример 2.2.1. Исследовать системы на совместность

а) b) c)

Решение:

a)

Имеем , так как

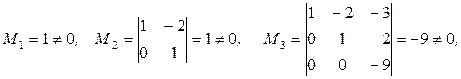
а окаймляющий минор четвертого порядка . Так как существует минор

то 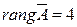. Таким образом, . Следовательно, по теореме 2.2.1 система несовместна.

 

b)

Здесь , так как среди ее миноров 2-го порядка есть отличные от нуля, например, , а миноров 3-го порядка нет. Аналогично, Итак, . Следовательно, система совместна. Так как количество неизвестных в системе меньше ранга матрицы, т.е. 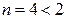, то система имеет бесконечное множество решений.

c)

Имеем . Следовательно, система совместна. Так как количество неизвестных равно рангу матрицы системы, т.е. , то по теореме 2.2.2, система имеет единственное решение.

Замечание 2.2.2. Рассмотренные в этом параграфе теоремы позволяют исследовать систему на совместность, а в случае совместной системы, установить является она определенной или неопределенной. Однако данные теоремы не дают практического способа отыскания всех решений системы. Этот вопрос будет изучен нами в дальнейшем.