Решение смешанной краевой задачи для неоднородного гиперболического уравнения
При нулевых граничных условиях
Рассмотрим вынужденные колебания однородной струны, закрепленной на концах, под действием внешней силы 
. Математически задача заключается в решении неоднородного уравнения гиперболического типа
 
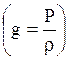
| (1.149) |
при однородных граничных условиях
 , 
| (1.150) |
и начальных условиях
 ,  .
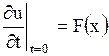| (1.151) |
Будем искать решение смешанной задачи (1.149)… (1.151) в виде суммы
 ,
| (1.152) |
где функция 
есть решение неоднородного уравнения
 ,
| (1.153) |
удовлетворяющее граничным условиям
 , 
| (1.154) |
и начальным условиям
 ,  ,
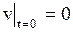| (1.155) |
а функция 
есть решение однородного уравнения
 ,
| (1.156) |
удовлетворяющее граничным условиям
 , 
| (1.157) |
и начальным условиям
 ,  .
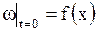| (1.158) |
Решение представляет вынужденные колебания струны, т.е. такие, которые совершаются под действием внешней силы, когда начальные возмущения отсутствуют.
Решение представляет свободные колебания, т.е. такие колебания, которые происходят только вследствие начального возмущения.
Непосредственной проверкой можно убедиться в том, что вследствие линейности уравнения, граничных и начальных условий сумма 
является решением исходной задачи.
Метод нахождения функции , т.е. решения задачи (1.156)… (1.158), рассмотрен в п. 1.28. Поэтому необходимо найти лишь функцию . Будем искать решение в виде ряда
 .
| (1.159) |
Для этой функции граничные условия (1.154) выполняются автоматически. Определим теперь функцию 
так, чтобы ряд (1.159) удовлетворял уравнению (1.153) и начальным условиям (1.155).
Подставляя ряд (1.159) в уравнение (1.153), получим
.
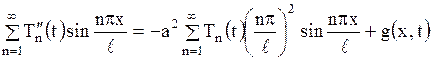Для удобства введем обозначение 
, тогда последнее уравнение можно переписать в виде
 .
| (1.160) |
Функция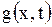 
, рассматриваемая как функция от 
при фиксированном 
, может быть разложена в ряд Фурье по синусам:
 ,
| (1.161) |
причем
 .
| (1.162) |
Сравнивая разложения (1.160) и (1.161), получим
 
| (1.163) |
Далее, из первого начального условия (1.155) следует, что
,
откуда
 .
| (1.164) |
Точно так же из второго начального условия (1.155) вытекает, что
 .
| (1.165) |
Таким образом, для определения нужно решить обыкновенное дифференциальное уравнение (1.163) с условиями (1.164) и (1.165).
Применяя к уравнению (1.163) метод вариации произвольных постоянных, найдем
.
Или подставляя вместо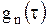 
его выражение (1.162), получим
 .
| (1.166) |
Подставляя найденное выражение для в ряд (1.159), получим искомое решение .
Итак, решение задачи (1.149)…(1.151) выражается в виде ряда
 ,
| (1.167) |
где коэффициенты определяются по формулам (1.166), а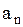 
и 
- по формулам (1.147) и (1.148).
Решение неоднородного гиперболического уравнения
при неоднородных граничных условиях.
(Общая первая краевая задача)
Рассмотрим вынужденные колебания ограниченной струны под действием внешней силы, причем концы ее не закреплены, а двигаются по заданному закону. Эта задача сводится к решению уравнения
|
| (1.168) |
с граничными условиями
 , 
| (1.169) |
и начальными условиями
,  .
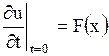| (1.170) |
Сформулированная задача (1.168)…(1.170) называется общей краевой задачей для уравнения колебаний. К решению этой задачи нельзя применить метод Фурье, так как граничные условия (1.169) неоднородны. Но эта задача может быть сведена к задаче с нулевыми граничными условиями.
Будем искать решение задачи (1.168)…(1.170) при помощи некоторой вспомогательной функции в виде
| ,
| (1.171) |
где подберем таким образом, чтобы задача нахождения функции была с однородными граничными условиями.
Дифференцируя (1.171) по и дважды и подставляя в (1.168), получим
.
Отсюда получаем, что функция будет определяться как решение уравнения
 ,
| (1.172) |
где
,
удовлетворяющее граничным условиям
 , 
| (1.173) |
и начальным условиям
| (1.174) |
Подберем функцию так, чтобы
, 
,
откуда находим, что
 ,  .
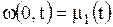| (1.175) |
В качестве можно взять любую непрерывную дважды дифференцируемую функцию, удовлетворяющую условиям (1.175). Например, может быть линейной относительно функцией вида
 .
| (1.176) |
Таким образом, общая первая краевая задача для функции 
сведена к краевой задаче для функции при нулевых граничных условиях. Для нахождения функции имеем уравнение
| ,
| (1.177) |
где
,
с граничными условиями
| ,
| (1.178) |
и начальными условиями
| (1.179) |
Метод решения задачи (1.177)…(1.179) изложен в п. 1.29.