Проверку гипотезы проведём на конкретном примере.

Пример. Производятся конденсаторы. Случайная величина X – ёмкость конденсатора. На основании опыта известно, что X имеет нормальное распределение с s²=25 пФ². Номинальное значение ёмкости равно 100 пФ.

Необходимо извлечь выборку объёма n=20 и решить вопрос о том, действительно ли в среднем значение ёмкости равно 100 пФ, и производство не нуждается в переналадке.

Решение.

1. Нулевая гипотеза H₀: m₀=100.

2. Альтернативная гипотеза H₁: m₀¹100 пФ.

Зам. В принципе могли быть альтернативы m₀>100 пФ или m₀<100 пФ, но нас интересует вопрос: нет ли отклонения от номинала.

3. Выбираем уровень значимости a=0,05. Это означает, что мы готовы в 5% случаев ошибочно рекомендовать переналадку оборудования, т.е. будет отвергнута нулевая гипотеза. Если мы не хотим мириться с таким процентом ошибки 1 – го рода, то можем выбрать, например, a=0,01, но мы тогда должны быть готовы к увеличению числа ошибок 2 – го рода, вследствие чего возрастут жалобы потребителей на несоответствие ёмкости указанному номиналу.

4. Как было сказано выше, критерием для проверки гипотезы может служить функция (статистика)

поскольку в неё входят m₀ и s.

5. Функция распределения критерия при условии выполнения нулевой гипотезы является нормальной, а значение выборочного среднего не должно сильно отличаться от 100 и соответственно случайная величина не должна сильно отличаться от нуля.

6. Для построения критической области следует воспользоваться таблицей нормального закона распределения и найти Ua при a=0.05. Оно равно 1.96. Критическая область будет располагаться на крыльях распределения (см. рис.1), попадания куда маловероятно (т. Чебышева).

Вывод. Так как 1- ,

то ÞФ(Ua)-Ф(-Ua)=2Ф(Ua)-1. Отсюда Ф(Ua)=1-a/2=1-0,025=0,975. Входим в таблицу нормального распределения и для вероятности 0,975 находим Ua=1,96.

Площадь кривой плотности распределения в заштрихованных крыльях (левее т. -1,96 и правее точки 1,96, см. рис.1), согласно выбранному уровню значимости, должна составлять 0,05. Критическими значениями u_1-α/2=1,96 и u_α/2=-1,96 отделяются критические области от области принятия гипотезы. Альтернативная гипотеза H₁ была использована при определении расположения критических областей. Поскольку она не различает отклонения математического ожидания в большую или меньшую сторону, критические области должны включать оба крыла распределения (см. рис.1). Если бы альтернативная гипотеза имела, например, вид m₀<100 пФ, то критическая область располагалась бы целиком слева.

Рис. 1. Критическая область и область принятия гипотезы

Пусть извлечена выборка X объёма n=20 (см. табл.1)

Таблица 1

Вычислим выборочное среднее 101,1 пФ, а затем значение критерия (1)

0.09.

Выборочное значение критерия Uв=0,09 попадает в область принятия гипотезы [-1,96; 1,96]. Следовательно, нет основания отвергнуть гипотезу H₀ и переналаживать производство.

2. Проверка гипотезы о значении среднего нормальной
совокупности с неизвестной дисперсией

В примере, рассмотренном выше, было сделано искусственное предположение о том, что нам известна дисперсия s². В реальных ситуациях это почти всегда не так.

Пусть нам задана выборка X={x₁, x₂,…, x_n} из нормальной N(a, s²) совокупности. Спрашивается, как проверить гипотезу a=a₀, если s² неизвестна. Когда объём выборки мал (n<30), а дисперсия генеральной совокупности неизвестна, для проверки гипотезы H₀: a=a₀ используют статистику

, где – выборочное среднее; s – выборочное среднее квадратичное отклонение; – исправленное выборочное среднее квадратичное отклонение.

Ели нулевая гипотеза верна, случайная величина t распределена по закону Стьюдента с n-1 степенями свободы.

Зададимся уровнем значимости α и определим t_α, из соотношения

1- , где t(x) – распределение Стьюдента. Обозначим через t_в выборочное значение статистики, вычисленное по выборке наблюдений. Если и вычислены на основе нашей выборки, то принимаем гипотезу H₀: a=a₀, если

и отвергаем её, когда

.

Возьмём данные из предыдущего примера (см. табл. 1): , s²=30.5, s=5.5. Находим значение критерия

По таблице распределения Стьюдента находим t_α. Входные данные: α=0.05, k=n-1=19, значение . Гипотезу H₀: a=100 – принимаем, так как 0.08<2.093.

Замечание. В статистических пакетах (например, Statgraphics) находят значение вероятности , обозначаемое как P-value. Если P-value больше уровня значимости α, то гипотезу принимают; в противном случае – отклоняют. В нашем случае гипотезу принимаем, так как 0,936>0,05.

Проверка гипотезы о значении среднего с использованием
пакета StatGraphics

Запускаем пакет Statgraphics [5] и выберем пиктограмму Untitled в левом нижнем углу рабочего поля и инициализируем новую электронную таблицу для ввода данных и вводим данные из таблицы 1. Вызываем процедуру вычисления описательных статистик Describe/Numeric Data/one variable analysis. Появится окно для задания анализируемой переменной (рис.3). Далее, на дополнительной панели

Рис.3. Окно для задания переменной X.

инструментов нажмите кнопку табличных опций и выберите процедуру Summary Statistics. На экране появится окно с полученными результатами. Для того чтобы расширить выводимый список, нажмите правую копку мыши и выберите из контекстного меню пункт Pane Options. Откроется диалоговое окно, изображённое на рис.4.

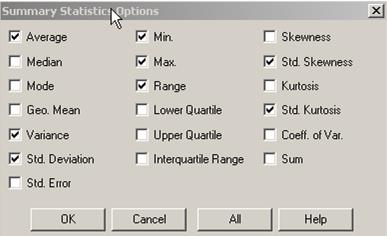
Рис.4. Флажки для задания общих статистик выборки

Для проверки гипотезы о значении среднего щелкаем мышкой по кнопке (вторая слева) и в появившимся окне Tabular Options выбираем опцию Hypothesis Tests (см. рис. 5)

Рис. 5. Выбираем опцию Hypothesis Tests

После появления панели устанавливаем параметры своей задачи: значение математического ожидания равного 100 и уровня значимости α равного 0,05. Для этого нажимаем на правую клавишу мыши и в появившемся окне выбираем Pane Options и устанавливаем свои значения (см. рис. 6) и нажимаем кнопку ОК. Появится результат решения задачи (см. рис.7).

Рис. 6 Установка параметров задачи

Рис. 7. Результаты решения задачи

Наша гипотеза согласуется с экспериментальными данными.

Как было сказано выше, гипотезу о значении математического ожидания можно проверить через понятие "доверительный интервал". Открываем окно Tabular Options и выбираем опцию Confidence Intervals (доверительные интервалы) см. рис. 8.

Рис. 8. Выбор процедуры "Доверительный интервал"

Рис. 9. Результаты вычисления доверительного интервала

Согласно данным рис. 9 доверительный интервал для среднего равен [97.5; 102.7] и содержит значение =101.1. Следовательно, гипотезу о том, что среднее равно 100 принимаем.