ЛАБОРАТОРНАЯ РАБОТА №2
ИЗМЕРЕНИЕ ЕМКОСТИ КОНДЕНСАТОРОВ. ИЗУЧЕНИЕ ЗАКОНОВ ПОСЛЕДОВАТЕЛЬНОГО, ПАРАЛЛЕЛЬНОГО И СМЕШАННОГО СОЕДИНЕНИЙ КОНДЕНСАТОРОВ
ЦЕЛЬ РАБОТЫ: ознакомиться с одним из методов измерения электроемкости конденсатора, измерить величину неизвестной емкости, убедиться в справедливости законов параллельного и последовательного соединений конденсаторов.
Приборы и ПРИНАДЛЕЖНОСТИ: набор конденсаторов, выпрямитель ВС-24М, двухполюсной переключатель, микроамперметр, соединительные провода.
Краткая теория
Рассмотрим конденсатор с емкостью С, который включен в схему (рис. 1). Если переключатель находится в положении 1, то происходит зарядка конденсатора через сопротивление R. Ток зарядки (разрядки) является квазистационарным, так как величина тока в каждый момент времени остается одинаковой во всех сечениях неразветвленной проводящей цепи. Токи проводимости при зарядке конденсатора не являются замкнутыми токами, так как заряды не перемещаются через диэлектрик конденсатора.
Будем считать, что сопротивление R включает в себя и внутреннее сопротивление источника. Тогда, согласно второму закону Кирхгофа:
,
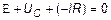где
E - ЭДС источника;
U C - мгновенное значение напряжения, создаваемого зарядами конденсатора.
I - мгновенное значение тока, создаваемого зарядами конденсатора.
Считая, что:
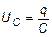и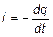 
,
получим:
.
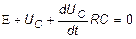Данное уравнение является дифференциальным уравнением первого порядка с постоянными коэффициентами. Разделяя переменные и интегрируя, получим:
.
Постоянная интегрирования А зависит от начальных условий. Если считать, что отсчет времени начинается с момента замыкания ключа (t =0 и U C=0), то А =E.
|
|
Отсюда:
.
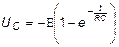Знак минус показывает, что при зарядке напряжение конденсатора направлено против ЭДС источника. В начальный момент времени t =0 напряжение на конденсаторе равно нулю. С увеличением времени напряжение на конденсаторе непрерывно увеличивается и асимптотически приближается к ЭДС источника (рис. 2,а).
Зависимость тока зарядки от времени имеет вид:
.
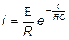Ток имеет наибольшее значение в начальный момент времени и асимптотически стремится к нулю в процессе зарядки конденсатора (рис. 2,б).
Если переключатель перебросить в положение 2, конденсатор начинает разряжаться через сопротивление R. Для процесса разрядки уравнение имеет вид:
.
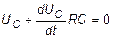Решая данное уравнение с учетом начальных условий (t =0, U C= U 0), получим:
.
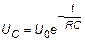В процессе разрядки конденсатора напряжение на конденсаторе уменьшается и асимптотически приближается к нулю (рис. 3,а). Зависимость тока разрядки от времени имеет такой же вид (рис. 3б):
.
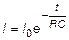Полученные формулы показывают, что теоретически процессы зарядки и разрядки протекают бесконечно большое время. На практике процесс считают установившимся, когда разность между изменяющейся величиной и ее пределом составляет 5% от полного изменения. Время переходного процесса можно определить, полагая, например,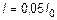 
:
.
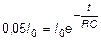Отсюда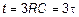 
.
Величина t= RC называется временем релаксации или постоянной времени цепи. Эта величина показывает время, в течение которого ток зарядки или разрядки конденсатора уменьшается в е =2,71 раз и составляет 0,37 своего максимального значения.
Ход работы
ЗАДАНИЕ 1. Измерение емкости конденсаторов.
|
|
1. Собрать цепь по схеме (рис. 4) включив в цепь конденсатор с известной емкостью.
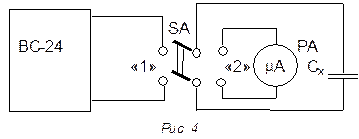
2. Установить на выходе выпрямителя напряжение 4 В.
3. Установить переключатель в положении "1" (конденсатор заряжается).
4. Установить переключатель в положении "2" (конденсатор разряжается через микроамперметр). При этом микроамперметр показывает ток разряда конденсатора, который пропорционален величине заряда конденсатора при данном напряжении.
5. Повторите пп. 3,4 несколько раз и среднее значение тока разряда для данного напряжения запишите в таблицу.
6. Повторите пп. 3-5, изменяя напряжение на выходе выпрямителя. Шаг и пределы изменения напряжения выбрать самостоятельно.
7. Включите в цепь конденсатор с неизвестной емкостью Сx (Отсоединив предварительно конденсатор с известной емкостью).
8. Повторите пп. 2-6 для конденсатора с неизвестной емкостью. Результаты запишите в таблицу.
9. Повторите пп. 2-6 для другого конденсатора с неизвестной емкостью Сx.
10. Вычислите неизвестную емкость конденсатора. (Формулу для вычисления Сx вывести самостоятельно.)
11. Определите погрешности измерений.
Таблица 1