Определение. Множество точек  пространства, координаты которых в некоторой прямоугольной декартовой системе координат удовлетворяют уравнению
пространства, координаты которых в некоторой прямоугольной декартовой системе координат удовлетворяют уравнению
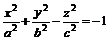 , (5.1)
, (5.1)
называют двуполостным гиперболоидом.
Из уравнения (4.1) следует, что если на двуполостном гиперболоиде лежит точка  , то на нем лежат и точки
, то на нем лежат и точки  с любым набором знаков
с любым набором знаков  и
и  . Это означает, что для поверхности (5.1) начало координат – точка
. Это означает, что для поверхности (5.1) начало координат – точка  – является ее центром симметрии и называется центром двуполостного гиперболоида; оси координат являются осями симметрии и их называют главными осями; координатные плоскости являются плоскостями симметрии и называются главными плоскостями этой поверхности.
– является ее центром симметрии и называется центром двуполостного гиперболоида; оси координат являются осями симметрии и их называют главными осями; координатные плоскости являются плоскостями симметрии и называются главными плоскостями этой поверхности.
Рассмотрим сечения поверхности (5.1) плоскостями, параллельными координатным плоскостям.
1) Сечения двуполостного гиперболоида плоскостями  определяются уравнениями
определяются уравнениями
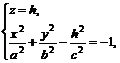 или
или 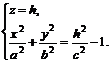 (5.2)
(5.2)
а) Если 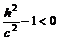
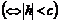 , то система (5.2) действительных решений не имеет. Это означает, что плоскость
, то система (5.2) действительных решений не имеет. Это означает, что плоскость  в этом случае не пересекает поверхность (5.1). Следовательно, в пространственной полосе, определяемой неравенствами
в этом случае не пересекает поверхность (5.1). Следовательно, в пространственной полосе, определяемой неравенствами 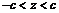 , точки рассматриваемой поверхности отсутствуют.
, точки рассматриваемой поверхности отсутствуют.
б) Если 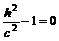
 , то система (5.2) имеет одно единственное решение
, то система (5.2) имеет одно единственное решение  при
при  и одно единственное решение
и одно единственное решение  при
при  .
.
Точки  и
и  пересечения поверхности (5.1) с осью
пересечения поверхности (5.1) с осью  называют вершинами двуполостного гиперболоида.
называют вершинами двуполостного гиперболоида.
в) Если 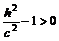
 , то система (5.2) равносильна соотношениям
, то система (5.2) равносильна соотношениям
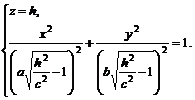 (5.3)
(5.3)
Соотношения (5.3) определяют эллипс, расположенный в плоскости  . Его центр находится в точке
. Его центр находится в точке  , оси параллельны координатным осям
, оси параллельны координатным осям  и
и  . Длины полуосей
. Длины полуосей
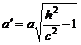 и
и 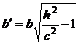
изменяются от  до
до  при изменении
при изменении  от
от 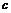 до
до  соответственно.
соответственно.
2) Сечения двуполостного гиперболоида (5.1) плоскостями  определяются уравнениями
определяются уравнениями
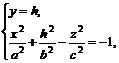 или
или 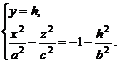 (5.5)
(5.5)
Так как 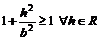 , то соотношения (5.5) равносильны системе
, то соотношения (5.5) равносильны системе
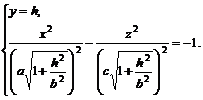 (5.6)
(5.6)
Уравнения (5.6) определяют гиперболу, расположенную в плоскости  . Ее центр находится в точке
. Ее центр находится в точке 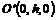 , действительная ось параллельна оси
, действительная ось параллельна оси  , мнимая – оси
, мнимая – оси  . Длины полуосей
. Длины полуосей
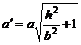 и
и 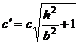
изменяются от  и
и 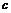 до
до  при изменении
при изменении  от
от 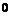 до
до  соответственно.
соответственно.
3) Сечения двуполостного гиперболоида плоскостями 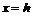 рассматриваются аналогично предыдущему случаю.
рассматриваются аналогично предыдущему случаю.
Приведенные рассуждения и сделанные при этом выводы позволяют получить представление о форме рассматриваемой поверхности (Рис. 11).
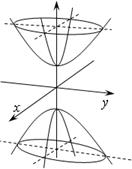
Рис. 11. Двуполостный гиперболоид
Если в уравнении (5.1) 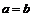 , то эту поверхность называют двуполостным гиперболоидом вращения, поскольку он может быть получен вращением гиперболы
, то эту поверхность называют двуполостным гиперболоидом вращения, поскольку он может быть получен вращением гиперболы
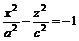
вокруг ее действительной оси  (Рис. 12).
(Рис. 12).
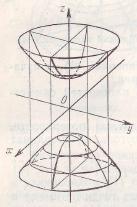
Рис. 12. Двуполостный гиперболоид вращения.
Конус второго порядка
Определение. Множество точек  пространства, координаты которых в некоторой прямоугольной декартовой системе координат удовлетворяют уравнению
пространства, координаты которых в некоторой прямоугольной декартовой системе координат удовлетворяют уравнению
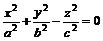 , (6.1)
, (6.1)
называют конусом второго порядка.
Из уравнения (6.1) следует, что для этой поверхности начало координат – точка  – является ее центром симметрии и называется вершиной конуса; оси координат являются осями симметрии и их называют главными осями; координатные плоскости являются плоскостями симметрии и называются главными плоскостями этой поверхности.
– является ее центром симметрии и называется вершиной конуса; оси координат являются осями симметрии и их называют главными осями; координатные плоскости являются плоскостями симметрии и называются главными плоскостями этой поверхности.
Нетрудно показать, что если на конусе (6.1) лежит точка 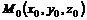 (не совпадающая с его вершиной), то на нем лежат и все точки прямой
(не совпадающая с его вершиной), то на нем лежат и все точки прямой 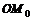 , проходящей через точку
, проходящей через точку 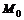 и его вершину
и его вершину 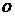 . В самом деле, если
. В самом деле, если  - произвольная точка, лежащая на прямой
- произвольная точка, лежащая на прямой 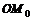 , то
, то

и потому
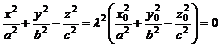
Таким образом, поверхность (6.1) образована прямыми, проходящими через начало координат.
Определение. Прямые, целиком лежащие на поверхности, зазывают ее прямолинейными образующими.
Вообще, линейчатую поверхность, все прямолинейные образующие которой проходят через одну точку (ее вершину), называют конической (или конусом).
Направляющей конуса называют произвольную расположенную на нем линию, обладающую тем свойством, что любая прямолинейная образующая пересекает ее в одной и только одной точке.
1) Сечения конуса (6.1) плоскостями  определяются уравнениями
определяются уравнениями
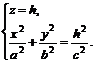 (6.2)
(6.2)
а) Если  , то системе (6.2) удовлетворяют координаты только одной единственной точки – ее вершины
, то системе (6.2) удовлетворяют координаты только одной единственной точки – ее вершины  .
.
б) Если 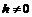 , то соотношения (6.2) равносильны системе
, то соотношения (6.2) равносильны системе
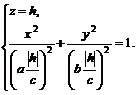 (6.3)
(6.3)
Уравнения (6.3) определяют эллипс, расположенный в плоскости  . Его центр находится в точке
. Его центр находится в точке  , оси параллельны координатным осям
, оси параллельны координатным осям  и
и  . Длины полуосей
. Длины полуосей
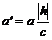 и
и 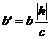
изменяются от 0 до  при изменении
при изменении  от 0 до
от 0 до  соответственно.
соответственно.
2) Сечения конуса (6.1) плоскостями  определяются уравнениями
определяются уравнениями
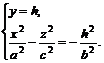 (6.4)
(6.4)
а) Если  , то система (6.4) равносильна соотношениям
, то система (6.4) равносильна соотношениям
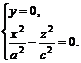 (6.5)
(6.5)
Уравнения (6.5) определяют пару пересекающихся прямых
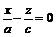 (а) и
(а) и 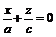 , (б) (6.6)
, (б) (6.6)
расположенных в плоскости  и целиком лежащих на конусе.
и целиком лежащих на конусе.
б) Если 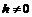 , то соотношения (6.4) равносильны системе
, то соотношения (6.4) равносильны системе
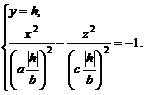 (6.7)
(6.7)
Уравнения (6.7) определяют гиперболу, расположенную в плоскости  . Ее центр находится в точке
. Ее центр находится в точке 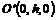 , действительная ось параллельна оси
, действительная ось параллельна оси  , мнимая – оси
, мнимая – оси  . Длины полуосей
. Длины полуосей
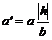 и
и 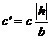
изменяются от  до
до  при изменении
при изменении  от
от 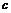 до
до  соответственно.
соответственно.
3) Сечения конуса плоскостями  рассматриваются аналогично предыдущему случаю.
рассматриваются аналогично предыдущему случаю.
4) Рассмотрим сечения поверхности (6.1) плоскостями 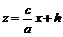 , которые параллельны прямолинейной образующей (6.6а) конуса. Эти сечения определяются уравнениями
, которые параллельны прямолинейной образующей (6.6а) конуса. Эти сечения определяются уравнениями
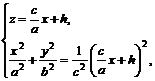
которые после несложных преобразований принимают вид:
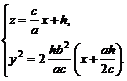 (6.8)
(6.8)
Уравнения (6.8) определяют параболу, расположенную в плоскости 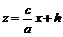 . Ее вершина находится в точке
. Ее вершина находится в точке 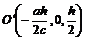 , а ось параллельна прямолинейной образующей (6.6а).
, а ось параллельна прямолинейной образующей (6.6а).
Таким образом, различными плоскими сечениями конуса второго порядка являются и эллипс, и гипербола и парабола. На этом основании их обычно называют коническими сечениями.
Приведенные рассуждения и сделанные при этом выводы позволяют получить представление о форме рассматриваемой поверхности (Рис. 13).
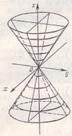
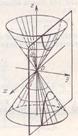
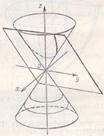
а) эллипс б) гипербола в) парабола
Рис. 13. Конус и его сечения.