Процесс последовательного исключения неизвестных называется прямым ходом метода Гаусса. После завершения прямого хода у нас появляется возможность вычислить неизвестную переменную, находящуюся в последнем уравнении. С ее помощью из предпоследнего уравнения находим следующую неизвестную переменную и так далее. Процесс последовательного нахождения неизвестных переменных при движении от последнего уравнения к первому называется обратным ходом метода Гаусса.
А лгоритм метода Гаусса.
1. Записываем расширенную матрицу. Расширенная матрица системы – это матрица коэффициентов при неизвестных плюс столбец свободных членов.
2. После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Цель элементарных преобразований – привести матрицу к ступенчатому (треугольному) виду.
3. После получения ступенчатой матрицы систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса – чтобы найти значения неизвестных.
Примеры:
1. Решить систему уравнений
методом Гаусса. Решение. Рассмотрим расширенную матрицу и приведем ее к треугольному виду, выполняя операции над строками:
  
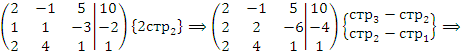Полученная матрица описывает систему уравнений
эквивалентную исходной системе. Решение находится элементарно:
 
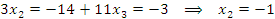Убедимся в том, что полученный набор  обращает каждое уравнение данной системы в тождество:
|
2. Решить систему уравнений
методом Гаусса. Решение. Преобразуем расширенную матрицу, производя элементарные операции над строками:
 
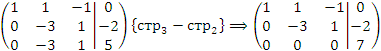Третья строка этой матрицы соответствует уравнению
не имеющему решений и, следовательно, система является несовместной.
|
3. Решить систему уравнений
методом Гаусса. Решение. Производя элементарные преобразования над строками, приведем расширенную матрицу к ступенчатой форме:
 
Выпишем соответствующую систему уравнений:
Последнее уравнение содержит две переменных, одну из которых нужно рассматривать в качестве свободного параметра. Назначим этому параметру произвольное значение 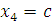 и выразим остальные переменные через c:
  
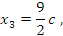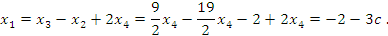Таким образом, общее решение системы имеет вид
Если подставить вместо c произвольное число, например нуль, то мы получим частное решение:  .
Подставляя c = 2, получаем другое частное решение:  .
Таким образом, данная система имеет бесконечное множество решений. Проверка: Подставим    и 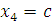в каждое уравнение системы:
 
Уравнения обратились в тождества.
|
ОБРАТИТЕ ВНИМАНИЕ.
При использовании метода Гаусса для решения систем линейных алгебраических уравнений следует избегать приближенных вычислений, так как это может привести к абсолютно неверным результатам. Рекомендуем не округлять десятичные дроби. Лучше от десятичных дробей переходить к обыкновенным дробям.
Дополнительные задания:
1. Решить систему методом Крамера, Гаусса или матричным методом:
1. 
2. 
3. 
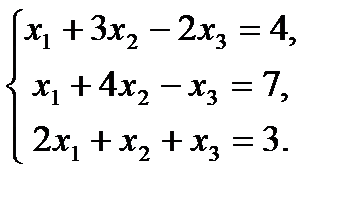
4. 
5. 
6. 
7. 
8. 
9. 