Требуется организовать перевозку продукции из пункта производства в пункт потребления так, чтобы весь товар из пунктов производства был вывезен, удовлетворяя потребность пунктов потребления и минимизировать стоимость перевозки
Математическая модель задачи:
- кол-во ед. продукта, перевозимого с i пункта производства в j пункт.
Кол – во продукта, вывезенного с i пункта произв.:
i = 1,2..m
Кол-во ед. продукта:
j = 1,2..n
Критерий – суммарные затраты:
F = 
Свойства транспортной задачи:
Транспортная задача разрешима тогда, когда выполняемы условия баланса:
- закрытая тр. Зад.
Ранг матрицы ограничений тр. Зад. = m+n-1.
13. Открытые модели транспортной задачи. Принцип замыкания. Метод минимального элемента, метод северо-западного угла.
Транспортные задачи разделены на два вида: открытые и закрытые. Транспортная задача считается закрытой, когда сумма товаров у поставщиков равна сумме потребностей потребителей (
)
Открытые задачи делятся еще на два типа:
1) Сумма изготовленных товаров у поставщиков превышает потребности потребителей (
). В этом случае вводится фиктивный потребитель (столбец 
)
2) Суммарное количество потребностей превышает количество изготовленных товаров (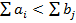
). В этом случае вводится фиктивный поставщик (строка 
)
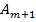Стоимость перевозки единицы грузы как к фиктивному потребителю, так и от фиктивного поставщика равна 0, т.к. по факту эти грузы не перевозятся. После преобразований с фиктивными фигурами модель задачи принимает открытый вид и можно спокойно проводить дальнейшие вычисления.
Метод минимального элемента:
Выбираем клетку, которая находится на «северо-западе», т.е. крайняя верхняя левая клетка (обозначим ее исходными символами i и j)
Начинаем считать.
Если 
, то ставим в клетку значение 
. При этом все остальные клетки строчки i будут заполнены прочерками.
Если 
, то ставим в клетку значение 
, а все клетки столбца j заполняем прочерками.
Если 
, то ставим в клетку значение, равное обоим числам, а во всех столбцах и строчках ставим прочерки.
Далее мы пересчитываем количество товаров и потребностей по формуле 
и 
. После чего заполняем клетку тем же способом, которая находится рядом с первоначальной и не имеет прочерка пока не будут заполнены все клетки опорного плана. Все клетки с прочерками являются небазисными, с числами – базисными.
Метод минимального элемента:
Суть данного метода во многом схожа с методом северо-западного угла. Только начальной точкой будет та, где цена перевозки наименьшая. Данный метод имеет некое превосходство, т.к. с его использованием можно с большей вероятностью приблизиться к плану перевозок, в котором затраты будут наименьшие.
14. Метод потенциала, цикл.
Метод потенциала заключается в следующем:
Пусть каждый из пунктов производства продукции вносит за перевозку единицы продукции некую сумму 
, и каждый из пунктов потребления так же платит некую сумму 
. Сами эти платежи передаются некоему третьему лицу («перевозчику»).
Тогда, перевозка из одной точки в другую стоит 
. Каждая из сторон платит за перевозку, что в сумме выходит 
.
Значение называется «псевдостоимостью» перевозки груза из пункта поставщика i в пункт потребителя j.
Оптимальным будет являться план, при котором потребитель и поставщик не будут переплачивать сверх объективной стоимости «перевозчику».
Цикл – последовательный набор клеток, в котором любые 2 клетки находятся в одной строке или столбце таблицы. И никакие 3 соседние клетки не находятся в одной строке или столбце. Первая и последняя клетка цикла должна быть из одной строки или столбца.
15. Конфликты интересов. Матричные игры с нулевой суммой.
«Нулевая сумма» - понятие, означающее, что выигрыш одного игрока в одной игре будет равен проигрышу другого игрока. Ярким примером такой игры будет «Орлянка». Ее суть состоит в том, что при выпадении одной стороны монеты выигрывает один игрок и наоборот. Если выигрывает первый, второй проигрывает ровно ту сумму, которую первый выиграл. Такая игра еще называется антагонистической.
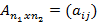
– объекты матричной игры с нулевой суммой, где
и 
- множество стратегий первого и второго игрока
- функция выигрыша первого игрока, ставящая в соответствие каждой паре стратегий действительное число, соответствующее полезности первого игрока при реализации данной ситуации
16. Смешанные стратегии, чистые стратегии.
Стратегия в игре – это план действий игрока в зависимости от ситуации в игре.
Чистая стратегия являет собой полную определенность, как будет действовать игрок.
Смешанная стратегия – это набор вероятностей, с которой игрок будет выбирать одну из чистых стратегий.
Смешанная стратегия первого игрока – вектор вероятности выбора стратегии p=(
)
Смешанная стратегия второго игрока q=(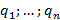
)
Чистая стратегия подразумевает под собой ход игрока с вероятностью 1. Такая стратегия возможна в играх «с полной информацией», где игрок заранее знает все исходы своих ходов и возможные ходы соперника. Примерами таких игр могут служить: шахматы, крестики/нолики, шашки.
Чистая стратегия даёт полную определённость каким образом игрок продолжит игру. В частности, она определяет результат для каждого возможного выбора, который игроку может придётся сделать. Пространством стратегий называют множество всех чистых стратегий доступных данному игроку.
Смешанная стратегия — является указанием вероятности каждой чистой стратегии. Это означает, что игрок выбирает одну из чистых стратегий, в соответствии с вероятностями заданными смешанной стратегией. Выбор осуществляется перед началом каждой игры и не меняется до её конца. Каждая чистая стратегия является частным случаем смешанной, когда вероятность данной чистой стратегии 1 и у всех других нулевая вероятность.
17. Оптимальное решение игры в смешанных стратегиях. Оптимальное решение игры в чистых стратегиях. Седловая точка.
Тройка (
) называется оптимальным решением в смешанных стратегиях игры, где
V = H(
) – цена игры, если
H(
) ≤ v = H() ≤ H(
)
Тройка (
) называется оптимальным решением в чистых стратегиях игры, если
Седловая точка матрица – это элемент, который минимален в своей строке и максимален в своем столбце.
18. Верхняя цена игры, нижняя цена игры.
Верхняя ценя цена равняется минимальному значению из возможных максимальных значений столбцов. 
, где 
– максимальное значение в слобце, j – количество столбцов.
Нижняя цена игры равняется максимальному значению из возможных минимальных значений строк. 
, где 
- минимальное значение в строке, i – количество строк.
В случае, когда верхняя цена равна нижней (
) – матричная игра решается в чистых стратегиях.
В противном случае (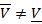
) – в смешанных стратегиях.
19. Основная теорема матричных игр.
Теорема фон Неймана. Каждая игра имеет хотя бы одно оптимальное решение в смешанных стратегиях.
Любая матричная игра разрешима в смешанных стратегиях, при этом:
| Maxmin H (p,q)= | min | Max H (p,q)=v |
| p | q | p |
() - оптимальное решение,
где 
- смешанная максиминная стратегия.
| min H (,q)=
| max | min H (p,q) |
| q | p | q |
Где 
- смешанная минимаксная стратегия
| max H (p, )=
| min | max H (p,q) |
| p | q | p |
20. Кооперативная игра, коалиции и дележи, С-ядро, цена Шепли.
Кооперативные игры получаются в тех случаях, когда, в игре n игроков разрешается образовывать определённые коалиции.
Игра называется кооперативной, или коалиционной, если игроки могут объединяться в группы, беря на себя некоторые обязательства перед другими игроками и координируя свои действия.
Кооперативной игрой в форме характеристической форме называется пара G = (N,V) где N={1,2,...,n} – конечное множество, называемое множеством игроков.
V – функция ставящая в соответствие каждому непустому подмножеству множества N вещественное число,
V: 
, V-характеристическая функция.
Непустое подмножество S множества N называется коалицией.
Максимальной или главной коалицией называется коалиция состоящая из всех игроков.
Выигрыш любой коалиции может быть разделен. Игроки любой коалиции могут передавать друг другу побочные платежи в виде премии или взяток.
Цель игры решить какие коалиции будут образованы, какой доход они получат и как он будет распределен между игроками.
С-ядро (core) (произносится цэ-ядро) — принцип оптимальности в теории кооперативных игр, представляющий собой множество эффективных распределений выигрыша, устойчивых к отклонениям любой коалиции игроков, то есть множество векторов 
, таких, что:
и для любой коалиции 
выполнено:
где u – характеристическая функция.
Вектором Шепли кооперативной игры называется такое распределение выигрыша, в котором каждый игрок получает математическое ожидание своего вклада в соответствующие коалиции 
, при равновероятном возникновении упорядочений:
21. Основные понятия теории графов.
Тео́рия гра́фов — раздел дискретной математики, изучающий свойства графов.
Граф – это множество вершин (узлов), соединенных ребрами. В строгом определении графом называется такая пара множеств G = (V,E), где V – подмножество любого счетного множества, а Е – подмножество V x V
Вершина – точка, где могут сходиться/выходить рёбра и/или дуги. Множество вершин графа G обозначается V(G).
Ребро – линия, соединяющая две вершины графа.
Дуга – это ориентированное ребро.
Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей работы.
Критический путь – (1 определение) наиболее продолжительный путь в сетевых графиках. (2 определение) работы этого пути определяют общую продолжительность работы над проектом.
Сеть – это граф, в котором существует лишь одна вешина, обознающая источник и одна вершина, обозначающая сток.
Источник – вершина, с которой начинается граф.
Сток – конечная вершина графа.
22. Модели структурного баланса.
1. Неориентированный граф G = (V,E)
2. Знак цепи в графе – произведение знаков ребер, образующих цепь.
3. Модель структурного баланса – знаковый граф G = (V,E)
4. Положительный знак ребра – симпатия между группами a и b
5. Отрицательный знак ребра – антипатия между группами a и b
Типы отношений в группах из 3-х человек:
Теорема Харари.
Для знакового графа следующие утверждения эквивалентны:
1. Граф G сбалансирован.
2. Любые две цели между вершинами u и v имеют одинаковый знак.
3. Множество V можно разбить на 2 непересекающихся множества А и В так, что каждое положительное ребро соединяет вершины из одного множества и каждое отрицательное ребро из различных множеств.
23. Статусные конфликты.
Математическая модель – связный бесконтурный орграф D=(V,A) (данная математическая модель наилучшим образом определяет субординацию)
Наличие дуги из u к v означает, что элемент u является непосредственным начальником v.
Если из вершины u в вершину v, причем длина данного пути больше 1, то это означает, что u вышестоящий начальник над v.
Длина кратчайшего пути от u до v – уровень v относительно u
Мера статуса:
Свойства:
1) Если вершина u не имеет выходных дуг, 
2) 
- получается из орграфа D добавлением в граф (часть инфы отсутствует…) вершины непосредственно доставленной из вершины u, это означает, что если сотрудник получает что-то, то его статус повышается 
Введем функцию:
, где 
число вершин на k уровне, которые располагаются ниже вершин(ы) u.
24. Конфликты альтернатив.
Конфликт альтернатив возникает, когда необходимо выбрать наилучшую альтернативу из множества. Либо может возникнуть, когда необходимо нашу альтернативу упорядочить.
Считается, что информация задана в виде бинарного отношения (двойного/квадратного) предпочтения на множестве альтернатив с практической точки зрения означает, что принимаемые решения либо эксперты попарно сравнивают альтернативы и указывают наиболее предпочтительные.
Математическая модель:
Орграф T = (V,A) называют турнирным, если для любой пары вершин 
существует ровно одна дуга 
, либо 
Победитель турнира: 
ß максимальное число дуг.
Утверждение.
В турнире существует полный простой путь
– число выходных дуг для вершины u
Примеры:
25. Когнитивные карты конфликтных процессов.
Когнитивные карты конфликтных процессов используются для качественного описания динамики конфликтных ситуаций в сложных системах.
Когнитивные карты – это знаковые/взвешенные ориентированные графы, которые отображают элементы моделируемой системы и связи между ними.
Конфликтная проблематика состоит в определении устойчивости системы.
Элементы системы обозначаются вершинами орграфа.
Значимые связи обозначают дугами. (u,v) – элемент u непосредственно влияет на элемент v.
Элементам могут приписывать числовые значения.
Дуга (u,v): “+” или “-“.
Обратные связи – контуры.
Увеличение значения вершины u (+) влечет увеличение дуги v.
Два типа: положительные (положительная обратная связь) и отрицательные (отрицательная обратная связь).
Контур усиливает отношение тогда и только тогда, когда он положителен.
m – общее число всех контуров в графе i-го контура.
| Система бесконфликтна | Система конфликтна | |
| Система устойчива | -1 < R < 0 | 
|
| Система неустойчива | 
| 
|
26. Основные определения динамического программирования и постановка задачи.
Динамическое программирование – этот математический метод поиска оптимальных решений по управлению многошаговыми процессами, в которых состояние исследуемых систем изменяется во времени или поэтапно.
Отметим, что подобные процессы и системы широко распространены в реальном мире и управление ими является важным при решении управленческих задач.
Основные понятия и постановка задачи
Определение. Многошаговым процессом называется процесс, при котором происходит последовательный переход объекта или системы данного класса из одного состояния в другое.
Разделение процесса на отдельные последовательные шаги вытекают из естественных свойств процесс или вводится искусственно.
Важными системами являются управляемые системы, на состояние которых может влиять «лицо, принимающее решение».
Примеры задач динамического программирования:
- задача о ранце,
- задача о распределении ресурсов (финансовых, материальных и т.п.) между предприятиями с целью получения максимальной прибыли за определенный период времени,
- определение наиболее экономичного режима полета летательного аппарата,
- составление календарных планов ремонта и обновления технологического оборудования на предприятии,
- задача о прокладке наивыгоднейшего пути между двумя пунктами (требуется так провести дорогу из пункта А в пункт В, чтобы суммарные затраты на сооружение участка были минимальными)
27. Метод динамического программирования и его этапы. Принцип оптимальности Беллмана.