Определение 7. Функция  называется бесконечно малой в точке
называется бесконечно малой в точке  , если для любого
, если для любого 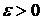 существует
существует  такое, что для всех
такое, что для всех  ,
,  и
и  выполняется
выполняется  , то есть
, то есть
 .
.
Замечание. Одна и та же функция при определенных значениях x является БМФ, а при других значениях – не является. Так как  , то
, то  есть бесконечно малая функция при
есть бесконечно малая функция при  , и
, и  не является БМФ при
не является БМФ при  , так как
, так как  .
.
Замечание. Аналогично можно дать определения бесконечно малых функций при  ,
,  ,
,  ,
,  ,
,  .
.
Приведем некоторые теоремы о бесконечно малых функциях, относящиеся к важным свойствам БМФ.
Теорема 1. (Основная теорема о бесконечно малых функциях).
Если функция имеет предел, то ее можно представить как сумму постоянной, равной ее пределу, и бесконечно малой функции.
Теорема 2. Алгебраическая сумма конечного числа бесконечно малых функций при 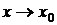 есть бесконечно малая функция.
есть бесконечно малая функция.
Теорема 3. Произведение ограниченной функции при 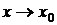 на бесконечно малую при
на бесконечно малую при 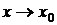 является бесконечно малой функцией при
является бесконечно малой функцией при 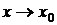 .
.
Теорема 4. Произведение конечного числа бесконечно малых функций при 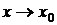 есть бесконечно малая функция.
есть бесконечно малая функция.
Важную роль в математическом анализе играют бесконечно большие функции.
Определение 8. Функция  называется бесконечно большой (ББФ) при
называется бесконечно большой (ББФ) при 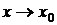 , если для сколь угодно большого числа
, если для сколь угодно большого числа 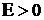 существует
существует  такое, что для всех
такое, что для всех  ,
,  таких, что при
таких, что при  выполняется
выполняется  .
.
Обозначение  .
.
Свойства бесконечно больших функций идентичны свойствам бесконечно малых функций.
Между бесконечно малыми и бесконечно большими функциями имеется следующая связь:
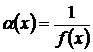 или
или  .
.
Доказательство следует из определения бесконечно малых (бесконечно больших) функций. (Рекомендуется доказать самостоятельно). Такая связь между бесконечно малыми и бесконечно большими функциями позволяет использовать естественную символическую запись, используемую для сокращения: для любого положительного числа а >0 пишут

Отметим, что на бесконечно большие функции свойства конечных пределов, связанные с арифметическими действиями над пределами, не всегда переносятся.
Например, если
 ,
,
то и

С другой стороны ничего нельзя утверждать о наличии или отсутствии предела разности функций, то есть
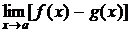 .
.
В таких случаях говорят о наличии неопределенности вида ∞─∞.
Для вычисления пределов функций применяется правило предельного перехода:
чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения функции, нужно в выражение функции вместо аргумента подставить его предельное значение.
Способы вычисления пределов.
I. Непосредственная подстановка.
Пример.  .
.
II. Раскрытие неопределенностей
Неопределенности типа 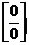 раскрываются:
раскрываются:
1) разложением на множители и сокращением:
Пример.  ;
;
2) переводом иррациональности из числителя в знаменатель и наоборот, домножением на сопряженный множитель:
Пример.
 ;
;
Пример.
 .
.
Имеем неопределенность вида  . Раскроем скобки и приведем подобные слагаемые.
. Раскроем скобки и приведем подобные слагаемые.
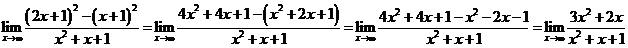 .
.
Получили неопределенность вида 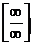 . Разделим числитель и знаменатель на
. Разделим числитель и знаменатель на 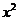 и так как при
и так как при  , получим
, получим  .
.