Распространение тепла в стержне

Оглавление

Введение. 3

1 Уравнения в частных производных. 3

2 Распространение тепла в стержне. 4

3 Метод Фурье для одномерного уравнения теплопроводности. Распространение тепла в ограниченном стержне. 6

4 Решение задачи спектральным методом.. 11

Заключение. 15

Список источников. 16

Введение

В данной работе рассматриваются методы решения уравнения распространения тепла в стержне. В первой части работы рассматриваются уравнения в частных производных. Эти уравнения называются основными уравнениями математической физики. Они описывают физические процессы, относящиеся к области механики сплошных сред. Именно этим и объясняется название курса "Уравнения математической физики". Во второй части речь идет об основных уравнениях математической физики полученных на основе общих законов физики, описывающие распространение тепла в стержне. Далее, более подробно, рассматривается метод Фурье для одномерного уравнения теплопроводности, так же известный как метод разделения переменных. В заключительной части работы описывается спектральный способ решения данной задачи, с использованием программного обеспечения Matlab/Octave.

Уравнения в частных производных

Уравнением с частными производными относительно функции u(x₁,…,x_n) называется уравнение, содержащее хотя бы одну из частных производных этой функции. Порядком уравнения с частными производными называется порядок наивысшей производной входящей в это уравнение. Дифференциальное уравнение с частными производными называется линейным, если искомая функция и ее частные производные входят в него линейно (т.е. в первой степени) [1]

Решение уравнения в частных производных может содержать произвольные функции, в отличие от обыкновенных дифференциальных уравнений, решение которых может содержать лишь произвольные постоянные.

Пример.

Очевидно, что функция U(x,y) = j(y) есть решение уравнения , где j(y) произвольная функция от y.

Наибольший практический интерес представляют дифференциальные уравнения второго порядка. В частности, линейное уравнение с частными производными второго порядка с искомой функцией U 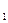(x ,x ,…,x ) от n независимых переменных имеет вид:

(1)

где a_i,j = a_j,i, i,j =1,2,…,n. a_i,j, b_i, c, f – есть функции x₁,x₂,…,x_n.

Если f(x_1,x₂,...,x_n) = 0, то уравнение (1) называется линейным однородным уравнением, в противном случае - линейным неоднородным.

Среди уравнений с частными производными второго порядка следует выделить три типа, которые для функций двух независимых переменных имеют

вид.

Волновое уравнение (уравнение гиперболического типа)	(2)
Уравнение теплопроводности или уравнение Фурье (уравнение параболического типа)	(3)
Уравнение Лапласа (уравнение эллиптического вида)	(4)

Распространение тепла в стержне

Основные уравнения математической физики получены на основе общих законов физики. Получим уравнение теплопроводности, рассматривая процесс теплопередачи в однородном ограниченном стержне длиной l. Будем считать,

0 x₁ x₂ l

что боковая поверхность теплоизолирована, а температура в поперечном сечении одинакова. Один конец стержня расположен в точке x = 0, тогда другой конец будет иметь координату x = l.

Пусть T(x,t) - температура в точке x в момент времени t.

Скорость распространения тепла (количество тепла протекающего через поперечное сечение стержня с абсциссой x за единицу времени) установлена опытным путем:

S - площадь сечения стержня;

λ-коэффициент теплопроводности.

Рассмотрим элемент стержня, заключенный между сечениями с абсциссой x ₁ и x₂. Обозначим D x = x ₂ – x ₁. Через сечение с абсциссой x ₁ за время D t пройдет количество тепла равное .

То же самое, для сечения с абсциссой x ₂: ,

где означает при x = x _1, а производная при x = x₂.

Приток тепла в рассматриваемый элемент стержня за время D t будет:

[ ] – [ ] @ l (5)

В выражении (5) применена теорема Лагранжа .

В результате этого притока тепла температура в рассматриваемом элементе стержня изменяется на величину D T, т.е.

DQ₁ -DQ₂ = С× r×Dx×S×DT

или DQ₁ -DQ₂ @ С× r×Dx×S × (6)

где С – теплоемкость вещества стержня;

r - плотность вещества стержня.

Приравнивая (5) и (6) получим: l = С× r×Dx×S×

Или = . Обозначим

Уравнение теплопроводности в стержне примет вид:

(7)

Это простейшее уравнение параболического типа.

Рассматривая процесс распространения тепла в 3-х мерном пространстве, где температура Т(x,y,z,t) является функцией координат (x,y, z) и времени t, можно получить уравнение теплопроводности в виде:

(8)

Если функция Т(x,y,z,t) не зависит от z, т.е. температура не зависит от z, то получим уравнение распространения тепла на плоскости:

= a ² ( + ). (9)

Коэффициент a ² имеет тот же смысл что и в уравнении (7).