(5 часов)
1.1 Задача о минимальном остове
1.1.1 Постановка задачи
1.1.1.1 Приведём постановку задачи о построении минимального остовного дерева (minimum-spanning-tree problem) (задачи о минимальном соединении). Имеется n городов, которые нужно объединить в единую телефонную сеть. Для этого достаточно проложить (n-1) телефонных линий между городами. Как соединить города так, чтобы суммарная стоимость соединений (телефонного кабеля) была минимальна?
1.1.1.2 Сформулируем задачу в терминах теории графов. Пусть дан связный, неориентированный граф G=(V, E) со взвешенными рёбрами, в котором V – множество вершин (городов), а E – множество рёбер (возможных попарных соединений городов). Пусть для каждого ребра {u,v} однозначно определено некоторое вещественное число ω(u,v) – его вес (длина или стоимость соединения); ω(…) называется весовой функцией. Задача состоит в нахождении такого связного ациклического подграфа T  G, содержащего все вершины, что суммарный вес его рёбер будет минимален.
G, содержащего все вершины, что суммарный вес его рёбер будет минимален.
Так как T связен и не содержит циклов, то он является деревом и называется остовным или покрывающим деревом (spanning tree). Остовное дерево T, у которого суммарный вес его рёбер  минимален, называется минимальным остовным или минимальным покрывающим деревом (minimum spanning tree).
минимален, называется минимальным остовным или минимальным покрывающим деревом (minimum spanning tree).
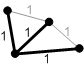
Для получения уникального минимального остовного дерева необходимо, чтобы весовые характеристики любой пары рёбер графа G были различны. Для примера, если все рёбра имеют единичный вес, то любое остовное дерево будет минимальным (с суммарным весом n-1, где n – количество вершин в графе) (рисунок 1.1).
| 
| 
| 
|

| 
| 
| 
|
Рисунок 1.1 – Все возможные минимальные остовные деревья для данного графа
1.1.1.3 У задачи построения минимального остовного дерева длинная и богатая история, которая берёт своё начало с работы Чекановского (Czekanowski) (1909г.). Первый и, наверное, простейший алгоритм восходит к Борувке (Boruvka), который в 1926-м году, намного раньше, чем появились первые компьютеры, и даже раньше, чем была создана конструктивная теория графов, представил своё решение данной задачи.
|
|
Другой известный алгоритм построения минимального остовного дерева восходит к Войтеху Ярнику (Vojtech Jarnik) (1930г.). Он больше известен под именем алгоритма Прима (Robert Prim). Р.Прим независимо от Ярника придумал его в 1956-м году и представил более подробное и детальное описание, чем первооткрыватель. Ещё раз этот алгоритм открыл Эдсгер Дейкстра (Edsger Wybe Dijkstra) в 1958-м году, но название осталось за Примом, т.к. у Дейкстры уже был алгоритм с его именем (поиск кратчайших путей в ориентированном графе). Этот алгоритм можно отнести к группе алгоритмов, построенных на наращивании дерева, начиная с корневой вершины. На каждом шаге существует не более одной нетривиальной (не состоящей из одной вершины) компоненты связности, и каждый к ней добавляется ребро наименьшего веса, соединяющее вершины компоненты с остальными вершинами.
Другой наиболее известный подход носит название алгоритма Крускала (Joseph Kruskal). Он был придуман автором в 1956-м году. Основная идея этого алгоритма такова: рёбра упорядочиваются (ранжируются) по весу; на каждом шаге к строящемуся остову добавляется самое лёгкое ребро, которое соединяет вершины из различных компонент. Таким образом, на каждом шаге строящееся множество состоит из одной или более нетривиальных компонент Ki (т.е. не состоящих из одной вершины), каждая из которых (Ki) является подграфом некоторого минимального остова Т.
|
|
1.1.2 Алгоритм Прима построения минимального остовного дерева
1.1.2.1 Стратегия алгоритма Прима построения минимального остовного дерева предельно ясна: на каждом шаге присоединяется ребро, минимальное по весу среди рёбер, соединяющих уже построенный фрагмент А минимального остова с вершинами, ещё не включёнными во фрагмент А. Для экономной реализации шагов этого процесса свяжем с каждой вершиной хÎVG (множество вершин графа G) две метки α(х) и β(х): α(х) – вес минимального по весу ребра, соединяющего вершину х с уже построенным фрагментом А минимального остова Т, а β(х) – имя второй вершины этого ребра, принадлежащей фрагменту А. Метки α(х) и β(х) позволяют быстро находить на каждом шаге ребро минимального веса. Кроме того, после присоединения очередной вершины v к фрагменту А метки остальных вершин графа (не вошедших во фрагмент) легко подкорректировать – для этого достаточно сравнить «старое» значение α(х) с ω(v,х) и выбрать из них мéньшее в качестве «нового» значения α(х). В приводимом ниже описании алгоритма построения минимального остова помимо α(х) и β(х) использованы следующие обозначения: VА, EА – множества соответственно вершин и рёбер строящегося фрагмента А минимального остова Т; Nx – окружение вершины х.
1.1.2.2 Алгоритм Прима построения минимального остова состоит из следующих шагов:
– шаг 1 – принять ЕА=Ø; VA={y}, где у – любая вершина из VG. Каждой вершине х≠у приписать метки α(х)=ω (х,у), если х  Ny, и α(х)=∞, если х
Ny, и α(х)=∞, если х  Ny; β(х)=у;
Ny; β(х)=у;
|
|
– шаг 2 – найти вершину, «ближайшую» к фрагменту А. Для этого выбрать вершину v*  VG\VA согласно условию
VG\VA согласно условию
 ;
;
– шаг 3 – увеличить фрагмент А. Пусть v’=β(v*). Изменить множества VA и ЕA, полагая VA=VAU{v*}; EA=EAU{v’,v*}. Включаемое во фрагмент А ребро {v’,v*} является безопасным (определение безопасного ребра мы дадим при изложении алгоритма Крускала);
– шаг 4 – если |VA|=n, т.е. если число вершин строящегося фрагмента минимального остова достигло числа вершин заданного графа G, то конец алгоритма, и рёбра, находящиеся в множестве ЕА, составляют минимальный остов ЕТ (в этом случае VA=VG). В противном случае – к следующему шагу;
– шаг 5 – для каждой вершины v  Nv*∩(VG\VA) изменить метки следующим образом: если α(v)> ω(v*,v), то α(v)= ω(v*,v); β(v)=v*; если же α(v)≤ ω(v*,v), то метку вершины v не менять. Перейти к шагу 2.
Nv*∩(VG\VA) изменить метки следующим образом: если α(v)> ω(v*,v), то α(v)= ω(v*,v); β(v)=v*; если же α(v)≤ ω(v*,v), то метку вершины v не менять. Перейти к шагу 2.
На рисунке 1.2 показана схема работы алгоритма Прима с корнем r.
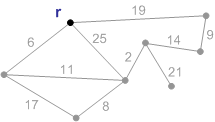 а – начальная фаза. Минимальный покрывающий лес состоит из корня r и пустого множества рёбер
а – начальная фаза. Минимальный покрывающий лес состоит из корня r и пустого множества рёбер
|  б – ребро с весом 6 является минимальным ребром, соединяющим корень с остальными вершинами. Добавляем его к минимальному остову
б – ребро с весом 6 является минимальным ребром, соединяющим корень с остальными вершинами. Добавляем его к минимальному остову
|
| Рисунок 1.2 – Пример построения минимального остова по алгоритму Прима | |
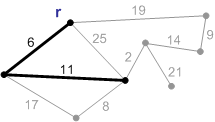 в – следующее безопасное ребро с весом 11. Добавляем его
в – следующее безопасное ребро с весом 11. Добавляем его
|  г
г
|
 д
д
|  е
е
|
 ж
ж
|  з – Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено
з – Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено
|
| Рисунок 1.2, лист 2 |
1.1.3 Алгоритм Крускала построения минимального остовного дерева
1.1.3.1 Алгоритм Крускала объединяет вершины графа в несколько связных компонент, каждая из которых является деревом. На каждом шаге из всех рёбер, соединяющих вершины из различных компонент связности, выбирается ребро с наименьшим весом. Необходимо проверить, что оно является безопасным. Безопасным ребром e относительно некоторой компоненты связности К из А назовём ребро с минимальным весом, ровно один конец которого лежит в К. Здесь А – некоторый подграф G, являющийся в то же время подграфом некоторого минимального остовного дерева T.
Заметим, что поскольку A не может содержать циклов, то на каждом шаге ребром соединяются либо различные компоненты связности, либо наращивается одна компонента связности, либо добавляется новая компонента.
На рисунке 1.3 представлена работа алгоритма Крускала.
 а – начальная фаза. Мини-мальный покрывающий лес пуст
а – начальная фаза. Мини-мальный покрывающий лес пуст
|  б – перебираем рёбра в порядке возрастания веса: первое ребро с весом 2. Добавляем его к А
б – перебираем рёбра в порядке возрастания веса: первое ребро с весом 2. Добавляем его к А
|
 в – следующее безопасное ребро с весом 6. Добавляем его
в – следующее безопасное ребро с весом 6. Добавляем его
|  г
г
|
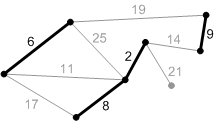 д
д
|  е
е
|
 ж
ж
| 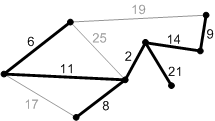 з – рёбра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено
з – рёбра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено
|
| Рисунок 1.3 – Пример построения минимального остова по алгоритму Крускала |
1.1.3.2 Итак, отметим основные отличия рассмотренных выше алгоритмов построения минимального остовного дерева. По алгоритму Прима строительство минимального остова ведётся с любой вершины и строящийся фрагмент А состоит всегда из одной компоненты связности (в самом начале – тривиальной, состоящей всего из одной корневой вершины) (см. рисунок 2). В то же время по алгоритму Крускала мы имеем дело в общем случае с несколькими нетривиальными компонентами связности, входящими во фрагмент А (на рисунке 3, б – одной; в и г – двумя; д – тремя компонентами связности).
1.1.4 Области применения
Областями применения задачи о минимальном остове являются:
– разработка сетей – ранее был приведен пример о соединении n городов в единую телефонную сеть с минимальной суммарной стоимостью соединений (это может быть транспортная сеть и т.п.);
– производство печатных плат – по аналогии с сетью: мы хотим соединить n контактов проводами с минимальной суммарной стоимостью. (Здесь стоит отметить, что задача о минимальном остовном дереве является упрощением реальности. В самом деле, если соединяемые контакты находятся в вершинах единичного квадрата, разрешается соединять любые его вершины, и вес соединения равен его длине, то минимальное покрывающее дерево будет состоять из трёх сторон квадрата. Между тем все его четыре вершины можно электрически соединить двумя пересекающимися диагоналями, суммарная длина которых будет равна 2√2, что меньше 3-х в первом случае);
– минимальное остовное дерево может использоваться для визуализации многоаспектных, многомерных данных, например, для отображения их взаимосвязи. Наука, и в частности биология, используют многомерные данные для группировки объектов, растений, животных. Минимальное остовное дерево позволяет разбивать их на взаимосвязанные классы, чётко отслеживая близкие по строению и характеристикам группы.
1.2 Задача о кратчайшем пути
1.1.2 Постановка задачи
1.1.2.1 Пусть G=(V,A) – ориентированный взвешенный граф. Задача о кратчайшем пути состоит в отыскании пути минимального веса, соединяющего заданные начальную и конечную вершины графа G при условии, что хотя бы один такой путь существует. Начальную и конечную вершины обозначим соответственно через s и t; (s, t)-путь минимального веса будем называть кратчайшим (s, t)-путём.
1.1.2.2 Вначале рассмотрим случай, когда веса всех дуг графа неотрицательны, т.е. ω(e)≥0 для каждой дуги е  А. В этом случае решение задачи о кратчайшем пути является существенно менее трудоёмким, чем в общем случае. Первый эффективный алгоритм построения кратчайшего пути в графе с неотрицательными весами дуг предложил Е.Дийкстра в 1959 г.
А. В этом случае решение задачи о кратчайшем пути является существенно менее трудоёмким, чем в общем случае. Первый эффективный алгоритм построения кратчайшего пути в графе с неотрицательными весами дуг предложил Е.Дийкстра в 1959 г.
1.1.3 Алгоритм Дийкстры поиска кратчайшего пути
1.1.3.1 На каждой итерации этого алгоритма всякая вершина v графа G имеет метку l(v), которая может быть постоянной либо врéменной. В первом случае l(v) – вес кратчайшего (s,v) -пути. Если же метка l(v) врéменная, то l(v) – вес кратчайшего (s,v) -пути, проходящего только через вершины с постоянными метками. Таким образом, врéменная метка l(v) является оценкой сверху для веса кратчайшего (s, v) -пути, и, став на некоторой итерации постоянной, она остаётся такой до конца работы алгоритма. Кроме метки l(v), с каждой вершиной v графа G, за исключением вершины s, связывается еще одна метка – θ(v). На каждой итерации θ(v) является номером вершины, предшествующей v в (s, v) -пути, имеющем минимальный вес среди всех (s,v) -путей, проходящих через вершины, получившие к данному моменту постоянные метки. После того как вершина t получила постоянную метку, с помощью меток θ(v) легко указать последовательность вершин, составляющих кратчайший (s,t) -путь.
Будем считать, что граф G задан матрицей весов либо списками смежности.
1.1.3.2 Алгоритм Дийкстры поиска кратчайшего пути состоит из следующих шагов:
– шаг 1 – положить l(s)=0 и считать эту метку постоянной. Положить l(v)=∞ для всех v  VG; v≠s, и считать эти метки временными. Положить р = s;
VG; v≠s, и считать эти метки временными. Положить р = s;
– шаг 2 – для всех v  Г(p), т.е. для всех вершин, смежных с вершиной р,с их врéменными метками выполнить следующее: если l(v)>l(p)+ω(p,v), то l(v)=l(p) + ω(p,v) и θ(v) = p, иначе l(v) и θ(v) не менять;
Г(p), т.е. для всех вершин, смежных с вершиной р,с их врéменными метками выполнить следующее: если l(v)>l(p)+ω(p,v), то l(v)=l(p) + ω(p,v) и θ(v) = p, иначе l(v) и θ(v) не менять;
– шаг 3 – пусть V’ – множество вершин с врéменными метками l. Найти вершину v* такую, что
 .
.
Считать метку l(v*) постоянной меткой вершины v*;
– шаг 4 – положить p=v*. Если p=t, то конец алгоритма [ l(t) – вес кратчайшего (s,t) -пути, а кратчайший путь P*=(s,..., θ3(t), θ2(t), θ(t), t) ]; иначе перейти к шагу 2.
Примечания
1 Как легко видеть, алгоритм применим к смешанным и, в частности, к неориентированным графам. Для этого достаточно каждое неориентированное ребро uv графа, имеющее вес ω(u,v), рассматривать как пару дуг (и,v) и (v,и) того же веса.
2 Если шаг 4 модифицировать так, чтобы алгоритм заканчивал работу только после получения всеми вершинами постоянных меток, то он будет строить кратчайшие пути из s в каждую из остальных вершин. Если к тому же вместе с превращением метки вершины v * в постоянную (см. шаг 3 алгоритма) заносить дугу (θ (v *), v *) в множество А*, т.е. раскрашивать дугу, то после окончания работы алгоритма граф D=(VG,А*) будет корневым ориентированным остовным деревом. Это дерево называют деревом кратчайших путей из вершины s графа G во все остальные вершины. Для любой вершины v  VG единственный (s,v) -путь в дереве D является кратчайшим (s,v) -путём в графе G.
VG единственный (s,v) -путь в дереве D является кратчайшим (s,v) -путём в графе G.
3 Алгоритм Дийкстры, модифицированный так, как указано в примечании 2, можно рассматривать как алгоритм построения дерева D кратчайших путей из вершины s графа G. С этой точки зрения алгоритм Дийкстры аналогичен алгоритму Прима построения минимального остова (см. подпункт 1.1.2.2). Действительно, построение дерева D состоит в последовательном увеличении уже построенного фрагмента путёмдобавления некоторой дуги, «выходящей» из этого фрагмента. При этом метки l и θ играют такую же роль, как и метки α и β в алгоритме Прима.
1.1.3.3 На рисунке 1.4 изображены пятькопий G k (k =  ) графа G, каждая из которых отражает ситуацию, сложившуюся после очередной итерации алгоритма. Около каждой дуги написан её вес. Вершинам копии Gk (k =
) графа G, каждая из которых отражает ситуацию, сложившуюся после очередной итерации алгоритма. Около каждой дуги написан её вес. Вершинам копии Gk (k =  ) приписаны метки, полученные ими в результате выполнения первых k итераций. Некоторые дуги обведены жирными линиями, т.е. отмечены (раскрашены). Добавление такой дуги (а, b) при переходе от Gk к Gk+1 означает, что вершина b получила свою метку l(b) из а и эта метка стала постоянной на (k+1)- йитерации. Вершина t в нашем примере получает постоянную метку последней, и отмеченные дуги графа G5 образуют дерево кратчайших путей из s.
) приписаны метки, полученные ими в результате выполнения первых k итераций. Некоторые дуги обведены жирными линиями, т.е. отмечены (раскрашены). Добавление такой дуги (а, b) при переходе от Gk к Gk+1 означает, что вершина b получила свою метку l(b) из а и эта метка стала постоянной на (k+1)- йитерации. Вершина t в нашем примере получает постоянную метку последней, и отмеченные дуги графа G5 образуют дерево кратчайших путей из s.
1.1.3.4 При решении многих задач возникает необходимость отыскания в невзвешенном графе (s,t) -пути с минимальным количеством дуг. Такой путь, очевидно, можно найти с помощью алгоритма Дийкстры. Для этого достаточно присвоить всем дугам графа G веса, равные 1, и применить алгоритм Дийкстры. Проследим работу алгоритма в этой ситуации, обращая особое внимание на последовательность, в которой вершины графа G получают постоянные метки. Очевидно, что вначале постоянные метки l=1 получат все вершины множества Г (s). Затем метка l=2 будет присвоена концам дуг, выходящих из Г (s). Вообще, постоянную метку l=k получают ещё не помеченные вершины, являющиеся концами дуг, исходящих из вершин с метками l=k-1. Этот процесс обхода (и присвоения меток) вершин графа называют поиском в ширину в графе. По окончании поиска в ширину метка l(х) вершины х равна минимальному числу дуг в (s,x)- пути. Как и ранее, сам этот путь определяется метками θ.
1.1.3.5 Перейдем теперь к рассмотрению общей ситуации. Будем считать, что в графе G допускаются дуги отрицательного веса. Предлагаемый ниже алгоритм строит в таком графе кратчайшие пути между всеми парами вершин графа при условии, что в графе нет отрицательных контуров (контуров отрицательного веса). Если же такой контур в графе имеется, то алгоритм сообщает об этом факте и прекращает работу, оставляя задачу отыскания кратчайшего пути нерешённой. Будем считать, что граф G, |G|=n, задан матрицей весов W =| |ωij ||, т.е. ωij=ω(i,j), если (i,j)  AG, и ωij=∞ в противном случае. Кроме того, полагаем ωii= 0 для
AG, и ωij=∞ в противном случае. Кроме того, полагаем ωii= 0 для
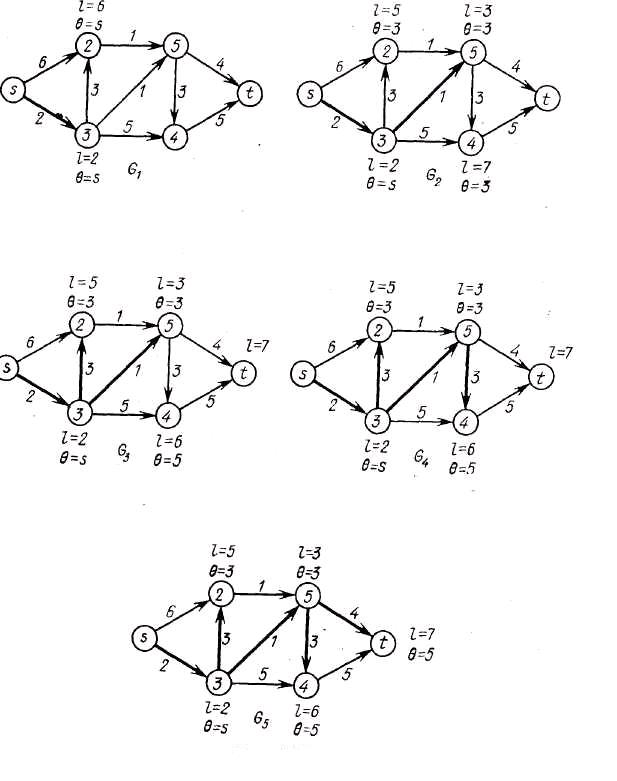
Рисунок 1.4 – Пример построения дерева кратчайших путей по алгоритму Дийкстры
всех i =l, 2,..., п. Алгоритм основан на следующих соображениях. Пусть i, j, k – три любые вершины графа G, и мы хотим получить (i,j) -путь, кратчайший среди (i,j) -путей, не содержащих внутренних вершин, отличных от k. Очевидно, что для этого достаточно выбрать мéньшую из двух величин ωij и ωik + ωkj, которая и будет весом такого (i,j) -пути. Если зафиксировать k и проделать эту операцию [назовём её тернарной (трёхместной) операцией или t-операцией, применённой к индексу k ]для всех пар (i,j), то получим матрицу W’ =|| ω’ij ||, y которой ω’ij= min {ωij,ωik + ωkj}. В этом случае говорят, что тернарная операция осуществляется для вершин i, j по вершине k. Алгоритм строит такую последовательность матриц W°, W1,..., Wn, где W°=W, что матрица Wm получается из матрицы Wm-1 применением t -операции к индексу т и матрице Wm-1. Если в графе G нет отрицательных контуров, то элемент ωijm матрицы Wm при каждом т равен весу кратчайшего (i,j)- пути, все внутренние вершины которого принадлежат множеству {1, 2,..., т }. Таким образом, последняя из этих матриц, т.е. матрица Wn, содержит весá кратчайших путей между всеми парами вершин графа. Для того чтобы после окончания работы алгоритма иметь возможность быстро найти кратчайший путь между любой парой вершин, будем на k- йитерации вместе с матрицей Wk строить матрицу Рk =|| рijk| |. Вначале полагаем рij0=i (i,j=  ). Далее, на k- йитерации полагаем рijk = рijk-1, если ωijk = ωijk-1 и рijk = k, если ωijk=ωikk-1 + ωkjk-1. Таким образом, pijk – номер вершины, предшествующей вершине j в текущем (i,j) -пути, т.е. в кратчайшем (i,j) -пути, все внутренние вершины которого содержатся в множестве {1, 2,..., k }. Матрица Рп =|| pijn| | играет ту же роль, что и метки θ в алгоритме Дийкстры. С помощью этой матрицы кратчайший (i,j) -путь L(i,j) определяется следующим образом: L(i,j)=(i,..., j3, j2, j1, j), где j1 = рijn, j2 = рij 1 n, j3 = рij 2 n,….
). Далее, на k- йитерации полагаем рijk = рijk-1, если ωijk = ωijk-1 и рijk = k, если ωijk=ωikk-1 + ωkjk-1. Таким образом, pijk – номер вершины, предшествующей вершине j в текущем (i,j) -пути, т.е. в кратчайшем (i,j) -пути, все внутренние вершины которого содержатся в множестве {1, 2,..., k }. Матрица Рп =|| pijn| | играет ту же роль, что и метки θ в алгоритме Дийкстры. С помощью этой матрицы кратчайший (i,j) -путь L(i,j) определяется следующим образом: L(i,j)=(i,..., j3, j2, j1, j), где j1 = рijn, j2 = рij 1 n, j3 = рij 2 n,….
1.1.3.6 Алгоритм Флойда отыскания кратчайших путей между всеми парами вершин (с помощью тернарных операций) состоит из следующих шагов:
– шаг 1 – W0=W, k= 1, P°=||рij0|| где pij0=i (i,j=  );
);
– шаг 2 – выполнить для всех i,j=  : если ωijk-1<ωikk-1+ωkjk-1, то ωijk = ωijk-1, рijk = рijk-1. Иначе ωijk =ωikk-1+ωkjk-1, pijk=k;
: если ωijk-1<ωikk-1+ωkjk-1, то ωijk = ωijk-1, рijk = рijk-1. Иначе ωijk =ωikk-1+ωkjk-1, pijk=k;
– шаг 3 – если для некоторого l, 1≤l≤ n, ωllk<0, то конец алгоритма (в графе имеется отрицательный контур, включающий вершину l; он строится с помощью вспомогательной матрицы). Иначе перейти к шагу 4;
– шаг 4 – k=k+1. Если k = n +1, то конец алгоритма (Wn =|| ωijn| | –матрица весов кратчайших путей, определяемых с помощью матрицы Рп= || рijn| |). Иначе перейти к шагу 2.
Заметим, что последовательность вершин, по которым проводятся тернарные операции, не имеет значения для конечного результата; главное, чтобы они были проведены по всем вершинам графа. Также отметим, что при проведении тернарных операций по k -й вершине элементы матриц W и Р, лежащие в k -й строке и в k -м столбце, не пересчитываются.
Примечания
1 Алгоритм будет применим к смешанным графам, если каждое неориентированное ребро заменить на две дуги того же веса. При этом следует учесть, что неориентированное ребро отрицательного веса сразу приводит к отрицательному контуру.
2 Алгоритм «отказывается» строить кратчайшие пути, когда в графе G имеются отрицательные контуры. В этом случае задача отыскания кратчайшего пути между двумя произвольными вершинами (или между всеми парами вершин) становится неразрешимой.
3 Если вспомогательную матрицу P°=||рij0|| (см. шаг 1 алгоритма) транспонировать, т.е. pij0=j (i,j=  ), то элемент рijn матрицы Рп будет указывать вершину, непосредственно следующую за вершиной i в кратчайшем пути из вершины i в вершину j.
), то элемент рijn матрицы Рп будет указывать вершину, непосредственно следующую за вершиной i в кратчайшем пути из вершины i в вершину j.
4 Если граф G неориентированный, то все матрицы Wk являются симметричными, поэтому достаточно вычислять элементы, находящиеся только выше (либо только ниже) главной диагонали.
5 Алгоритм Флойда позволяет отыскать в графе все отрицательные циклы. Если мы проводим тернарную операцию по k -й вершине и получили для i- йвершины ωiik<0 (таких отрицательных элементов матрицы W может получиться несколько при проведении тернарной операции), то i -я вершина принадлежит некоторому ориентированному циклу с отрицательной длиной, который строится с помощью вспомогательной матрицы Рk. Если k < n, то мы возвращаемся к исходным матрицам W0 и P° и продолжаем проводить тернарные операции по оставшимся вершинам графа до получения следующего(их) отрицательного диагонального элемента матрицы W и т.д. до тех пор, пока не проведём тернарные операции по всем n вершинам графа.
1.1.3.7 Ниже приведены результаты выполнения каждой из четырёх итераций алгоритма для графа, изображённого на рисунке 1.5.

Рисунок 1.5 – Орграф с отрицательными весами дуг

Найдём, например, с помощью матрицы Р4 кратчайший (2, 1)-путь: р214 =4, р244 =3, р234 =2.Следовательно, (2, 3, 4, 1) – кратчайший (2, 1)-путь.
1.1.3.8 Исходное предположение в алгоритме Дийкстры состояло в неотрицательности длин дуг исходного графа. Действительно, применение рассмотренного алгоритма (см. подпункт 1.1.3.2) к графу, изображённому на рисунке 1.6, даёт ошибочный результат: в качестве кратчайшего пути будет указан путь, состоящий из дуги (s,t), не являющийся таковым.
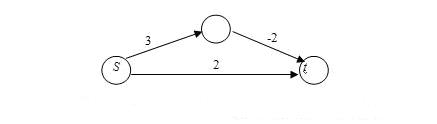
Рисунок 1.6 – Пример графа с отрицательным весом дуги, для которого алгоритм Дийкстры даёт неверный результат
Задачу поиска кратчайшего пути в графе с отрицательными весами дуг (кроме алгоритма в подпункте 1.1.3.6, ищущего кратчайшие пути между любой парой вершин в графе) решает алгоритм Форда, представляющий собой модификацию алгоритма Дийкстры. Модификация алгоритма Дийкстры состоит в следующем:
– на шаге 2 пересчёт величин l(v) производится для всех вершин, а не только для неокрашенных вершин, т.е. вершин с врéменными метками. Следовательно, числа l(v) могут уменьшаться как для неокрашенных, так и для окрашенных вершин, т.е. вершин с постоянными (по алгоритму Дийкстры) метками;
– если для некоторой окрашенной вершины v происходит уменьшение величины l(v), то с этой вершины и инцидентной ей окрашенной дуги окраска снимается, т.е. снимается выделение дуги;
– процедура заканчивается только тогда, когда все вершины окрашены и когда после выполнения шага 2 ни одно из чисел l(v) не меняется.
Алгоритм Форда не решает задачи поиска кратчайшего пути при наличии в исходном графе контура, имеющего отрицательную длину. Пример такого графа представлен на рисунке 1.7. Контур отрицательной длины образуют дуги (a,b), (b,a). Длина контура равна 3 – 4 = - 1; повторяя этот контур, можно получить путь со сколь угодно малой по величине длиной.

Рисунок 1.7 – Граф, содержащий контур отрицательной длины
Для обнаружения контура отрицательной длины можно обычным образом применять алгоритм Форда, но в процессе его работы необходимо учитывать, сколько раз окрашиваются отдельные вершины. Как только число окрашиваний какой-либо вершины достигает n, где n – число вершин графа, процедуру можно остановить: исходный граф содержит контур отрицательной длины.
Варианты заданий
Задание №1
Для графа, представленного на рисунке 1.8, найти остовное дерево минимальной длины при помощи:
а) алгоритма Крускала;
б) алгоритма Прима.

Задание №2
Дана матрица L=[lij] расстояний между каждой парой вершин сети. Если lij=∞, то это означает, что в сети нет дуги, ведущей из вершины i в вершину j. Если lij=lji, то вершины i и j соединены неориентированным ребром длиной lij. Требуется по матрице L построить сеть и найти кратчайшие пути из вершины 1 во все остальные вершины сети.
| L= | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
Задание №3
При помощи алгоритма Флойда найти все циклы отрицательной длины в орграфе, представленном на рисунке 1.9.
 |