ПП 8. Предел ПОСЛЕДОВАТЕЛЬНОСТИ
Арифметическая прогрессия  – числовая последовательность – числовая последовательность  такая, что такая, что  ( ( – разность). – разность).
 . .
  . .
| Геометрическая прогрессия  – числовая последовательность – числовая последовательность 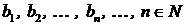 такая, что такая, что  и и 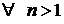 , ,  (
( – знаменатель). – знаменатель).
 . .
 . .
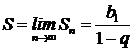 , если , если  (
( ). ).
|
{ xn } – последовательность xn.
 - формула общего члена последовательности.
- формула общего члена последовательности.
 - предел последовательности { xn }.
- предел последовательности { xn }.
Если { xn } бесконечно малая последовательность, то  .
.
Если  , то
, то  , где { an }– бесконечно малая последовательность.
, где { an }– бесконечно малая последовательность.
Если  и
и  ,то:
,то:
 ;
;
 ;
;
 ;
;
 , если
, если  ;
;
 ;
;
 .
.
Если для любого n 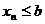 , то
, то  .
.
Если для любого n 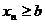 , то
, то  .
.
Если для любого n  и
и  , то
, то  .
.
Бесконечно малая последовательность ограничена.
Сумма двух бесконечно малых последовательностей есть последовательность бесконечно малая.
Разность двух бесконечно малых последовательностей есть последовательность бесконечно малая.
Произведение ограниченной последовательности на бесконечно малую есть последовательность бесконечно малая.
Произведение двух бесконечно малых последовательностей есть последовательность бесконечно малая.
Если элементы бесконечно малой последовательности не равны нулю, то последовательность  будет бесконечно большой.
будет бесконечно большой.
Если  – бесконечно большая последовательность и
– бесконечно большая последовательность и  , то последовательность
, то последовательность  – бесконечно малая.
– бесконечно малая.
 ,
,  .
.

Формула Стирлинга: 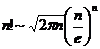 .
.
Неравенство Бернулли: 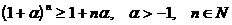 .
.
Формула бинома Ньютона:

 , где
, где 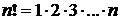 ,
,  .
.
Иначе,
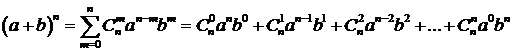 ,
,
где  – биномиальные коэффициенты.
– биномиальные коэффициенты.
Частный случай:

| пп 11. Теоретические Упражнения | ||
| ТУ ПП 8.№1. | Приведите примерограниченной снизу последовательности
РЕШЕНИЕ:
{ n2 } ограничена снизу, так как все члены этой последовательности удовлетворяют неравенству  . .
| { n2 } |
| ТУ ПП 8.№2. | Приведите примерограниченной сверху последовательности
РЕШЕНИЕ:
{ - n } = { – 1,–2,–3 ,…,– n,… }ограничена сверху, так как все члены этой последовательности удовлетворяют неравенству  . .
| { - n } |
| ТУ ПП 8.№3. | Приведите примерограниченной последовательности
РЕШЕНИЕ:
 ограничена, так как для всех nÎN имеет место система неравенств ограничена, так как для всех nÎN имеет место система неравенств  , т.е. M=1, m=0. , т.е. M=1, m=0.
| 
|
| ТУ ПП 8.№4. | Приведите примернеограниченной последовательности.
РЕШЕНИЕ:
1) { n2 } - при любом M>0 достаточно взять  ;
2) ;
2)  - несмотря на то, что все четные члены этой последовательности равны нулю, среди нечетных всегда найдется член, удовлетворяющий условию - несмотря на то, что все четные члены этой последовательности равны нулю, среди нечетных всегда найдется член, удовлетворяющий условию  для любого M>0. для любого M>0.
| |
| ТУ ПП 8.№5. | Покажите, что частное двух ограниченных последовательностей может быть как ограниченной, так и неограниченной последовательностью.
РЕШЕНИЕ:
Если  , а , а 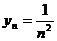 , то , то  – неограниченная последовательность, тогда как – неограниченная последовательность, тогда как  – последовательность ограниченная. – последовательность ограниченная.
|
| ТУ ПП 8.№6. | Приведите примерпоследовательности, не имеющей предела.
РЕШЕНИЕ:
Последовательность  не имеет предела, так как нельзя указать номер, после которого все члены последовательности окажутся в сколь угодно малой окрестности какого-либо числа. не имеет предела, так как нельзя указать номер, после которого все члены последовательности окажутся в сколь угодно малой окрестности какого-либо числа.
| |
| ТУ ПП 8.№7. | Приведите примерыбесконечно малых последовательностей.
РЕШЕНИЕ:
1) Бесконечно убывающая геометрическая прогрессия xn=qn, |q|<1, является бесконечно малой последовательностью, т.к. для любого e>0 из неравенства  следует, что при следует, что при  это неравенство выполнено. Таким образом, достаточно взять это неравенство выполнено. Таким образом, достаточно взять
 2) Последовательность
2) Последовательность  – бесконечно малая, т.к. ее элементы являются произведением элементов ограниченной последовательности – бесконечно малая, т.к. ее элементы являются произведением элементов ограниченной последовательности  и бесконечно малой последовательности и бесконечно малой последовательности  .
3) Последовательность .
3) Последовательность  – бесконечно малая, т.к. является суммой бесконечно малых последовательностей – бесконечно малая, т.к. является суммой бесконечно малых последовательностей  и и  .
4) Последовательность .
4) Последовательность  – бесконечно малая, т.к. является произведением бесконечно малой последовательности – бесконечно малая, т.к. является произведением бесконечно малой последовательности 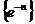 на бесконечно малую последовательность на бесконечно малую последовательность  . .
|
| ТУ ПП 8.№8. | При каких значениях a последовательности { na } являются бесконечно большими или бесконечно малыми последовательностями?
РЕШЕНИЕ:
1) Последовательности { na }, a>0 являются бесконечно большими, т.к. для любого M>0 из na следует, что если  ;
2) Последовательности { na }, a<0 являются бесконечно малыми, так как из | na|<e или ;
2) Последовательности { na }, a<0 являются бесконечно малыми, так как из | na|<e или 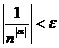 следует, что следует, что  или или  , т.е. существует номер , т.е. существует номер 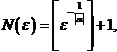 начиная с которого | na|<e.
Последовательности { na } при a>0 являются бесконечно большими, а при a<0 являются бесконечно малыми последовательностями.
начиная с которого | na|<e.
Последовательности { na } при a>0 являются бесконечно большими, а при a<0 являются бесконечно малыми последовательностями.
| |
| ТУ ПП 8.№9. | Бесконечно большая последовательность является неограниченной последовательностью. Выполняется ли обратное утверждение? РЕШЕНИЕ: Неограниченная последовательность 0, 4, 0, 8, 0, 12,… не является бесконечно большой, т.к. не все члены последовательности после некоторого n становятся больше произвольного M. | нет |
| ТУ ПП 8.№10. | Докажите, что  .
РЕШЕНИЕ:
Обозначим .
РЕШЕНИЕ:
Обозначим   . При n>1 an>0. Тогда из формулы бинома Ньютона . При n>1 an>0. Тогда из формулы бинома Ньютона 
 при при  . Так как . Так как  при при  , то , то  , откуда следует, что , откуда следует, что  . Так как . Так как  , то , то 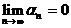 (см. ТУ ПП 8. №8)
Таким образом (см. ТУ ПП 8. №8)
Таким образом 
| |
| ТУ ПП 8.№11. | Докажите, что 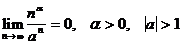 .
РЕШЕНИЕ:
Рассмотрим последовательность .
РЕШЕНИЕ:
Рассмотрим последовательность  и покажем, что и покажем, что  . Так как |a|>1, то |a|=1+b, b>0.
Тогда . Так как |a|>1, то |a|=1+b, b>0.
Тогда  (см. ТУ ПП 8. №10) (см. ТУ ПП 8. №10)  Таким образом, при
Таким образом, при  выполнены неравенства выполнены неравенства
 Так как
Так как  , то и , то и 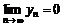 , а поскольку из , а поскольку из  следует, что следует, что 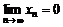 , то равенство доказано. , то равенство доказано.
| |
| ТУ ПП 8. №12. | Докажите, что  при |a|>1.
РЕШЕНИЕ:
Способ 1. Можно воспользоваться формулой Стирлинга при |a|>1.
РЕШЕНИЕ:
Способ 1. Можно воспользоваться формулой Стирлинга 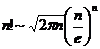 , которая указывает порядок роста n! при n ®¥. Тогда получаем: , которая указывает порядок роста n! при n ®¥. Тогда получаем:
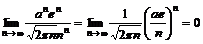 , т.к. , т.к.  , если n>ae.
Способ 2. Оценим значение , если n>ae.
Способ 2. Оценим значение  , записав его в виде: , записав его в виде:  ,
Пусть n>2k, а ,
Пусть n>2k, а 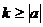 , тогда дробь , тогда дробь  и все следующие за ней дроби не превышают и все следующие за ней дроби не превышают 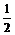 . Поэтому . Поэтому
 .
Так как .
Так как  , а , а
 ,
то и ,
то и  . .
| |
| ТУ ПП 8. №13. | Вычислите предел последовательности 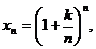  .
РЕШЕНИЕ:
Данная последовательность является ограниченной, т.к. .
РЕШЕНИЕ:
Данная последовательность является ограниченной, т.к. 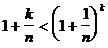 (из формулы бинома Ньютона), и, следовательно, (из формулы бинома Ньютона), и, следовательно,  ,
Кроме того, ,
Кроме того, 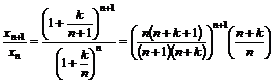 .
Так как (n+1)(n+k)= n (n+k+1)+ k, то .
Так как (n+1)(n+k)= n (n+k+1)+ k, то  , и в силу неравенства Бернулли , и в силу неравенства Бернулли
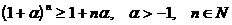 , имеем , имеем
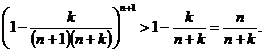 Таким образом,
Таким образом,  , т.е. последовательность { xn } возрастает, значит последовательность { xn } сходится. Для нахождения предела рассмотрим подпоследовательность с n=p×k. , т.е. последовательность { xn } возрастает, значит последовательность { xn } сходится. Для нахождения предела рассмотрим подпоследовательность с n=p×k.
 . .
|
| пп 8. ПреДЕЛЫПОСЛЕДОВАТЕЛЬНОСТЕЙ | ||
| ПП 8.№1. | Найдите формулу общего члена последовательности:
 Решение: Учитывая, что
Решение: Учитывая, что  ,
получаем ,
получаем  , n=0,1,2,…, т.е. нумерация членов последовательности начинается с нуля. Чтобы установить нумерацию с единицы, положим , n=0,1,2,…, т.е. нумерация членов последовательности начинается с нуля. Чтобы установить нумерацию с единицы, положим  , n=1,2,… , n=1,2,…
|  n=1,2,…. n=1,2,….
|
| ПП 8.№2. | Найдите все предельные точки последовательности  Решение:
Решение:

| 
|
| ПП 8.№3. | Найдите  , ,  , ,   для последовательности для последовательности  .
Решение:
Очевидно, что .
Решение:
Очевидно, что  . Первый множитель – . Первый множитель –  монотонно убывает с ростом номера, монотонно убывает с ростом номера,  ; второй множитель ; второй множитель  колеблется между 0 и 1. В соответствии с значениями второго множителя последовательность колеблется между 0 и 1. В соответствии с значениями второго множителя последовательность  может быть разбита на три монотонных подпоследовательности: может быть разбита на три монотонных подпоследовательности:  ;; ;;  , ,  . Легко видеть, что последовательность имеет три точки сгущения: . Легко видеть, что последовательность имеет три точки сгущения:  , ,  , ,  . .  ищем среди первых элементов подпоследовательностей, ищем среди первых элементов подпоследовательностей,  очевиден. очевиден.
|  , ,  , , 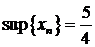 , ,  . .
|
| ПП 8.№4. | Укажите, какие из заданных последовательностей являются ограниченными, бесконечно большими и бесконечно малыми:
  .
Решение:
1) Последовательность .
Решение:
1) Последовательность 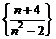 бесконечно малая, т.к. представляет собой сумму двух бесконечно малых последовательностей бесконечно малая, т.к. представляет собой сумму двух бесконечно малых последовательностей  и и 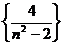 : последовательность : последовательность  бесконечно малая, т.к. бесконечно малая, т.к.  , а , а  – бесконечно большая; последовательность – бесконечно большая; последовательность 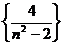 также бесконечно малая, т.к. также бесконечно малая, т.к.  – бесконечно большая.
2) Последовательность – бесконечно большая.
2) Последовательность 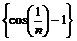 – ограниченная, т.к. при всех n – ограниченная, т.к. при всех n  .
3) Последовательность .
3) Последовательность  неограниченная, т.к. для любого M>0 можно указать неограниченная, т.к. для любого M>0 можно указать  такой, что при n>N, такой, что при n>N,  . .
| 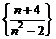 – бесконечно малая, – бесконечно малая,
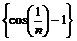 – ограниченная, – ограниченная,
 – неограниченная. – неограниченная.
|
| ПП 8.№5. | Пользуясь определением предела, докажите (укажите 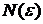 ), что ), что  , если , если   Решение:
Рассмотрим неравенство
Решение:
Рассмотрим неравенство  , или , или 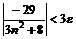 , или , или  , т.е. , т.е. 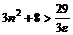 .
Тогда исходное неравенство выполняется при .
Тогда исходное неравенство выполняется при  , если , если  (Если (Если  , то неравенство выполняется для любого n).
Выбрав в качестве , то неравенство выполняется для любого n).
Выбрав в качестве  получим, что при всех
получим, что при всех  неравенство выполнено. неравенство выполнено.
| 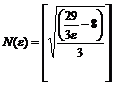
|
| ПП 8.№6. | Пользуясь определением предела, докажите, что  , если , если   (укажите (укажите 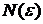 ).
Решение:
Докажем, что для последовательности ).
Решение:
Докажем, что для последовательности  по определению предела последовательности число по определению предела последовательности число 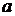 будет являться пределом, то есть выполняется утверждение: будет являться пределом, то есть выполняется утверждение:
 . .
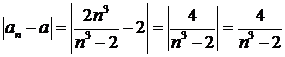 .
Возьмем произвольное .
Возьмем произвольное  и потребуем, чтобы, и потребуем, чтобы,  то есть выполнялось неравенство то есть выполнялось неравенство
 Решим это неравенство относительно
Решим это неравенство относительно 
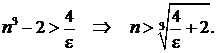 Положим
Положим  где где 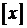 - целая часть числа - целая часть числа  , то есть выберем в качестве , то есть выберем в качестве 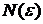 первое по величине натуральное число, которое превосходит действительное число первое по величине натуральное число, которое превосходит действительное число  , или равно ему, если это действительное число , или равно ему, если это действительное число  является целым.
Итак, существует номер является целым.
Итак, существует номер  , такой, что для номеров , такой, что для номеров 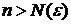 , ,
 что и требовалось доказать. что и требовалось доказать.
| 
|
| ПП 8.№7. | Пользуясь определением предела, докажите (укажите 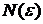 ), что ), что  , если , если   Решение:
Действительно, для любого e>0 неравенство
Решение:
Действительно, для любого e>0 неравенство  всегда выполнено, если всегда выполнено, если  .
В качестве N(e) достаточно взять целую часть числа .
В качестве N(e) достаточно взять целую часть числа  , увеличенную на единицу, т.е. , увеличенную на единицу, т.е. 
| 
|
| ПП 8.№8. | Пользуясь определением предела, докажите (укажите 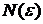 ), что ), что  , если , если 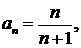  Решение:
Из неравенства
Решение:
Из неравенства  получаем получаем 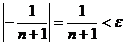 или или  . Выбирая . Выбирая  , если e£1, и N(e)=1, если e>1, получаем, что , если e£1, и N(e)=1, если e>1, получаем, что  . .
| 
|
| ПП 8.№9. | Вычислите предел числовой последовательности  .
Решение:
Числитель и знаменатель дроби стремятся к бесконечности, т.е. мы имеем неопределенность типа .
Решение:
Числитель и знаменатель дроби стремятся к бесконечности, т.е. мы имеем неопределенность типа  .
Выражение, стоящее под знаком предела, представляет собой отношение многочленов. Поделим числитель и знаменатель на .
Выражение, стоящее под знаком предела, представляет собой отношение многочленов. Поделим числитель и знаменатель на  в наибольшей степени ( в наибольшей степени (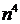 ): ):  Последовательности
Последовательности  - бесконечно малые, т.е. их пределы равны нулю. - бесконечно малые, т.е. их пределы равны нулю.
 .
Окончательно получаем .
Окончательно получаем
 . .
| 
|
| ПП 8.№10. | Вычислите предел числовой последовательности
 Решение:
Раскроем скобки, приведем подобные слагаемые и произведем деление числителя и знаменателя получившейся дроби на
Решение:
Раскроем скобки, приведем подобные слагаемые и произведем деление числителя и знаменателя получившейся дроби на  - наибольшую степень - наибольшую степень  . .

|
| ПП 8. №11. | Вычислите предел числовой последовательности  Решение:
Произведем деление числителя и знаменателя получившейся дроби на
Решение:
Произведем деление числителя и знаменателя получившейся дроби на  - наибольшую степень - наибольшую степень  . .

| |
| ПП 8. №12. | Вычислите предел числовой последовательности
 Решение:
Решение:




 
 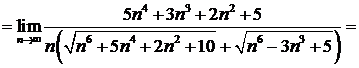


| 
|
| ПП 8. №13. | Вычислите предел:  .
Решение:
Выражение представляет неопределенность типа .
Решение:
Выражение представляет неопределенность типа  . Преобразуем подкоренные выражения, выделив возрастающие множители: . Преобразуем подкоренные выражения, выделив возрастающие множители:  , ,  , ,  , , 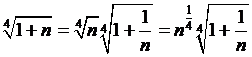 . Выносим в числителе и знаменателе старшие степени: . Выносим в числителе и знаменателе старшие степени:

| |
| ПП 8. №14. | Вычислите предел числовой последовательности  .
Решение:
В этом примере мы имеем дело с неопределенностью типа .
Решение:
В этом примере мы имеем дело с неопределенностью типа 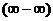 , т.к. , т.к.  и и  при при  .
Эту неопределенность можно устранить или превратить в неопределенность типа .
Эту неопределенность можно устранить или превратить в неопределенность типа  , вынеся за скобку старшую степень или домножая на сопряженное.
Способ 1: , вынеся за скобку старшую степень или домножая на сопряженное.
Способ 1:
 .
Выражение в скобках стремится к единице, а .
Выражение в скобках стремится к единице, а  . Отсюда следует, что предел не существует, т.е. . Отсюда следует, что предел не существует, т.е.
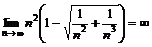 .
Способ 2: .
Способ 2:
 =
=  . .
| 
|
| ПП 8. №15. | Вычислите предел 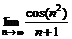 .
Решение:
Последовательность .
Решение:
Последовательность  есть произведение двух последовательностей есть произведение двух последовательностей  и и 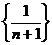 , из которых первая ограниченная, а вторая ¾ бесконечно малая. Следовательно, , из которых первая ограниченная, а вторая ¾ бесконечно малая. Следовательно,  . .
| |
| ПП 8. №16. | Вычислите предел  .
Решение: .
Решение:
 .
Последовательность .
Последовательность  бесконечно большая, т.к. бесконечно большая, т.к.  .
Следовательно, .
Следовательно,  . .
| 
|
| ПП 8. №17. | Вычислите предел  .
Решение:
В этом примере мы опять имеем дело с неопределенностью .
Решение:
В этом примере мы опять имеем дело с неопределенностью  .
Расписываем факториалы по формуле .
Расписываем факториалы по формуле 
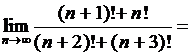   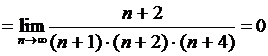 . .
| |
| ПП 8. №18. | Вычислите предел числовой последовательности  Решение:
Решение:


| |
| ПП 8. №19. | Вычислите предел числовой последовательности  Решение:
Числитель дроби представляет собой сумму
Решение:
Числитель дроби представляет собой сумму  первых членов арифметической прогрессии, которая равна первых членов арифметической прогрессии, которая равна
 поэтому поэтому
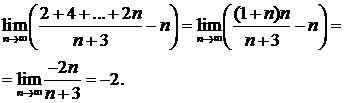
| -2 |
| ПП 8. №20. | Вычислите предел  .
Решение: .
Решение:
 Тогда Тогда
 . .
| е |
| ПП 8. №21. | Вычислите предел числовой последовательности 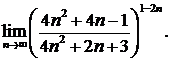 Решение:
Решение:
 
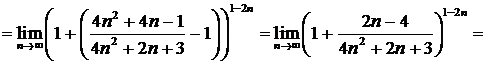


 
 
| 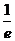
|
| ПП 8. №22. | Вычислите предел 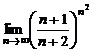 .
Решение: .
Решение:
 , , 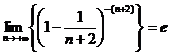 .
Таким образом, в последовательности .
Таким образом, в последовательности  основание стремится к e, а последовательность основание стремится к e, а последовательность  расходится и расходится и  при при  . Таким образом, получаем . Таким образом, получаем  . .
|