1. Уравнение непрерывности
Уравнение непрерывности выражает собой закон сохранения вещества в гидродинамике: разность количества жидкости, втекающей в данный промежуток времени в некоторый объем и вытекающей из него, равна приращению количества жидкости внутри данного объема.
Рассмотрим элементарный кубический объем
, (2.1)
показанный на рис. 2.1.
Пусть 
- масса вещества, переносимого вдоль оси Х за время dt.
В точке x:
. (2.2)
В точке x+dx:
. (2.3)
Приращение массы в рассматриваемом объеме за счет переноса вдоль оси X за промежуток времени dt:
. (2.4)
Вдоль оси Y:
. (2.5)
Вдоль оси Z:
. (2.6)
Полное приращение массы в объёме dV за время dt:
(2.7)
или
;
. (2.8)
С другой стороны, убыль массы в объеме dV за dt можно представить так
. (2.9)
Поэтому получим:
= 
. (2.10)
Следовательно, уравнение непрерывности для жидкости и газа имеет вид
(2.11)
Для плоской звуковой волны в дисперсной системе с объемной концентрацией частиц дисперсной фазы n уравнение непрерывности принимает вид:
, (2.12)
где ud – смещение частиц среды из положения равновесия.
2. Уравнение движения
В механике сплошных сред не учитывается то обстоятельство, что среда состоит из атомов и молекул. Рассматриваемый в ней малый объем мал в сравнении с размерами макроскопических тел, но достаточно велик по сравнению с расстоянием между молекулами (в акустике длина волны должна быть значительно больше средней длины свободного пробега молекул).
Рассмотрим уравнение движения идеальной среды (жидкости), в которой отсутствует вязкое трение, а также процессы теплопроводности.
Изучим движение жидкости в прямоугольном параллелепипеде, ребра которого параллельны осям координат (рис. 2.2). Обозначим координаты одной из вершин (ближайшей к началу координат) через x, y, z, координаты противоположной вершины – (x + dx), (y + dy), (z + dz). Ребра параллелепипеда, следовательно, равны dx, dy, dz.
Плотность жидкости r зависит от координат x, y, z и времени t.
На левую грань действует сила:
. (2.13)
На правую грань действует сила:
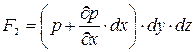, (2.14)
где p - давление в жидкости.
Алгебраическая сумма проекции этих сил на оси x, y, z соответственно равны
;
; (2.15)
.
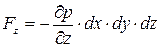Рассматриваемая частица испытывает ускорение
.
В данном случае необходимо взять полную производную от сложной функции, так как координаты частицы также зависят от времени, то есть
.
Имеем
. (2.16)
На основании второго закона Ньютона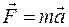 
, или в проекциях на оси:
;
; (2.17)
,
где r - плотность среды.
Следовательно, проекции вектора ускорения на оси координат равны:
;
; (2.18)
В векторном представлении имеем:
. (2.19)
Полученное уравнение является уравнением движения идеальной жидкости.
Уравнение движения для вязкой сжимаемой жидкости (уравнение Навье-Стокса) представляет 2-й закон Ньютона применительно к элементарному объему сплошной среды:
, (2.20)
где ηS - сдвиговая вязкость, ηV - объемная вязкость.
Отметим, что использованные в уравнениях (2.11) и (2.20) математические операторы в развернутом представлении имеют вид
;
(2.21)
3. Уравнение механического состояния
К числу важнейших в механике сплошных сред уравнений относится уравнение, выражающее зависимость давления в веществе от его плотности:
. (2.22)
Мы будем называть это уравнение уравнением механического состояния (в теории магнетизма, как будет сказано ниже, используется уравнение магнитного состояния). Для идеальных газов уравнением механического состояния является уравнение Менделеева – Клапейрона, а для адиабатного процесса уравнение адиабаты (уравнение Пуассона).
Уравнение механического состояния для газов в случае адиабатного процесса имеет вид
, (2.23)
где V - объем газа; γ - коэффициент Пуассона.
Поскольку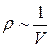 
, то можно записать
. (2.24)
В звуковой волне невозмущенные значения давления p0 и плотности ρ0 получают малые приращения δp и δρ. Из (2.24) следует
, (2.25)
откуда
. (2.26)
Таким образом, относительное приращение давления пропорционально относительному приращению плотности.
Применительно к жидким системам не удается получить универсальное уравнение состояния. Причиной этого является близость молекул друг к другу, в результате чего определяющую роль в формировании упругих свойств жидкости играют силы межмолекулярного взаимодействия, которые в каждой жидкости носят сугубо индивидуальный характер. Приходится использовать эмпирическое соотношение между плотностью ρ и давлением p. При малых амплитудах колебаний между приращением объема Δ V и давления Δ p (плотности Δ ρ или давления Δ p) существует линейная зависимость
; (2.27)
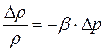, (2.28)
где коэффициент пропорциональности 
носит название сжимаемости и имеет размерность Па-1.
Соотношения (2.27) и (2.28) можно рассматривать как подобие закона Гука применительно к жидкостям. Значения сжимаемости различно для различных жидкостей и определяется опытным путем. Поэтому уравнение механического состояния для жидкостей, записанное в виде
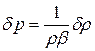, (2.29)
следует рассматривать как эмпирическое соотношение. Следует отметить также, что для жидкостей (исключение составляет вода) значение β, полученное при постоянной температуре βТ,всегда больше значения, полученного при отсутствии теплообмена βS. При распространении в среде ультразвуковой волны теплообмен между соседними фазами сжатия и растяжения практически не успевает произойти. Поэтому в уравнении (2.29) используется именно адиабатная сжимаемость βS.
. (2.30)
Применительно к твердым телам в теории упругости вместо зависимости p = f (ρ) вводятся уравнения, связывающие механическое напряжение и растяжение (деформацию) тела. Средней продольной деформацией называют отношение удлинения D xxx к первоначальной длине D x:
. (2.31)
Продольной деформацией в данной точке называется предел, к которому стремится это отношение при Dx®0, то есть
. (2.32)
Механическое напряжение s(x) – сила растяжения, приходящаяся на единицу площади поперечного сечения стержня.
Связь между напряжением и деформацией в линейном приближении описывается законом Гука
s = ES, (2.33)
где E – константа, характеризующая материал. Её называют модулем упругости (модулем Юнга).
Деформация и напряжение распространяются в твердом теле в виде волн с одной и той же скоростью.
В безграничном изотропном твердом теле возможны продольные волны того же типа, что и в жидкости или газе, и поперечные (сдвиговые волны). В твердых телах ограниченных размеров возможны волны и других мод (поверхностные, изгибные). Возможность распространения в веществе волн того или иного типа непосредственно связана с существованием определенного типа упругости (модуля упругости).
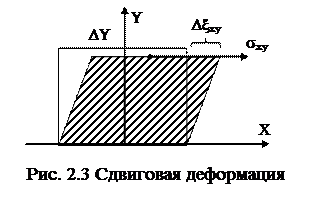Если нижнюю грань куба зафиксировать, то чтобы деформировать его в направлении оси x (т.е. сместить верхнюю грань на Dxxy), необходимо к его верхней грани приложить тангенциальную силу (напряжение sxy) (рис. 2.3).
В пределах упругой деформации выполняется закон Гука:
(2.34)
или при D y ®0:
. (2.35)
Коэффициент m представляет собой модуль сдвига.
Модули Е и m для твердых тел численно отличаются друг от друга. Обычно Е > m.
В ограниченных твёрдых телах (в частности, в пленках) могут распространяться также волны других типов. Из них основное значение имеют поверхностные волны (волны Рэлея), нормальные волны в слоях (волны Лэмба), изгибные волны [7].