Контрольная работа №1 (КР-1)
Задача 1-10
Необходимо решить систему уравнений (СЛАУ), представленную в задании в виде 
(1) СЛАУ необходимо решить тремя способами.
Первый способ – нахождение неизвестных (корней) СЛАУ с помощью определителей по формулам Крамера
где 
- основной определитель из коэффициентов левой части СЛАУ;
- первый вспомогательный определитель, который получают из основного определителя заменой первого столбца столбцом свободных членов.
, 
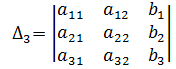- соответственно, второй и третий вспомогательные определители.
Определители третьего порядка можно вычислить:
а) способом треугольников;
б) способом дополнительных столбцов;
в) способом разложения по элементам строки или столбца определителя;
г) способом приведения определителя к треугольному виду.
Последний способ является наиболее общим и используется при вычислении определителей третьего и более высоких порядков. При этом обнуляются элементы определителя ниже главной диагонали с помощью его свойств. После приведения к треугольному виду определитель вычисляют как произведение его элементов, лежащих на главной диагонали.
Окончательную проверку правильности вычисления неизвестных (корней) производят подстановкой их в любое уравнение из СЛАУ (1). Если корни вычислены правильно, то в результате получим тождество.
Более подробно методика вычисления корней по формулам Крамера приведена в учебном пособии Вылегжанин Н.А., Пожидаев А.В. и др. Практикум по высшей математике для технических специальностей. Часть 1. – Новосибирск: издательство СГУПСа, 2011 – 228с; с. 40-45.
Пример решения СЛАУ с помощью определителей по формулам Крамера.
Пусть дана СЛАУ вида:
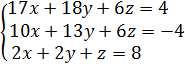
Составляем основной определитель ∆ из коэффициентов при неизвестных и вычисляем его согласно заданию разложением по первому столбцу без обнуления элементов:
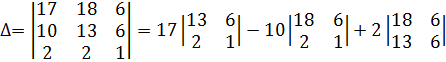
Проверяем основной определитель ∆ способом треугольников:
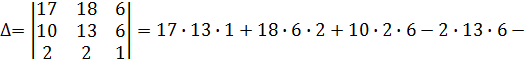
Составляем первый вспомогательный определитель и вычисляем его с предварительным приведением к треугольному виду. Равносильные математические преобразования проводим, используя свойства определителя.
= 
Проверяем ∆1 способом дополнительных столбцов
Составляем второй вспомогательный определитель и приводим к треугольному виду. Проверку преобразования строк определителя проводим, например, с помощью контрольного столбца.
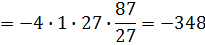
Аналогично находим ∆3 = 296
Замечание. С помощью контрольного столбца проверяется правильность выполнения действий при элементарных преобразованиях. Если действия выполнены, верно, то должно выполняться правило суммы: при любых элементарных преобразованиях i- ой строки сумма всех изменяемых элементов этой строки слева должна равняться числовому значению изменяемого i- го элемента контрольного столбца. Контрольный столбец можно вводить и исключать на любом этапе преобразований, если дальнейшие преобразования простые, и вы уверены в их правильности. Контрольные столбцы используются далее при решении СЛАУ способом Гаусса с расширенной матрицей.
Для окончательной проверки выбираем, например, третье уравнение, в которое подставляем найденные корни. Если в результате получаем тождество (левая и правая части уравнения совпадают), то корни найдены верно.
В нашем примере для проведения проверки выбираем третье уравнение и в него подставляем найденные корни СЛАУ.
Второй способ - Решение СЛАУ матричным способом (с помощью обратной матрицы)
Представляем СЛАУ в матричной форме
,
Из СЛАУ в матричной форме при 
находят матрицу неизвестных по форме 
, где 
– обратная матрица, соответствующая матрице A.
Для вычисления обратной матрицы часто используют следующие способы:
а) с помощью присоединённой (союзной) матрицы;
б) с помощью элементарных преобразований объединенной матрицы.
При выполнении второй части КР-1 воспользуемся первым способом. Методику элементарных преобразований матрицы, применяемую во втором способе, рассмотрим в примере для третьей части КР-1.
Алгоритм вычисления обратной матрицы с помощью присоединенной (союзной) матрицы:
1. Если определитель матрицы коэффициентов СЛАУ не равен нулю (
), то СЛАУ приводим к матричной форме 
.
2. Находим алгебраические дополнения (или миноры с соответствующими знаками) для всех элементов матрицы коэффициентов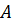 
и формируем из них присоединённую (союзную) матрицу 
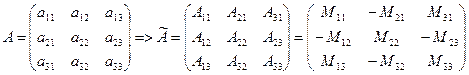
алгебраические дополнения элементов 
матрицы ;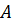
, где 
минор элемента 
матрицы 
Минор 
является определителем, который получают вычеркиванием i- ой строки и j- го столбца матрицы или определителя более высокого порядка.
3. Находим обратную матрицу по формуле
4. Правильность вычислений проверяем, используя равенство 
или 
. Применение последнего равенства является предпочтительным, так как матричное умножение при этом производится с целыми числами.
Пример решения конкретной СЛАУ с помощью обратной матрицы
Имеем СЛАУ
1. Определитель матрицы коэффициентов 
не равен нулю (
, см.1 способ), поэтому СЛАУ можно представить в матричной форме , где 
.
2. Находим миноры матрицы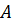
3. Составляем союзную матрицу.
4. Проверяем правильность вычисления матрицы
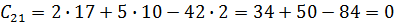
В результате получаем:
Союзная матрица найдена верно.
5. Находим обратную матрицу 
и определяем корни СЛАУ:
Корни СЛАУ, найденные первым и вторым способами совпадают.
Третий способ - Решение СЛАУ методом Гаусса с расширенной матрицей
Этот метод является наиболее общим и применяется для решения всех типов СЛАУ, имеющих решение.
Для решения неоднородной СЛАУ, представленной в матричной форме , используем следующий алгоритм:
1. Объединяем матрицу коэффициентов 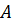и матрицу-столбец свободных членов 
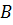, и получаем расширенную матрицу
2. С помощью элементарных преобразований расширенную матрицу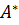 
приводим к ступенчатому виду:
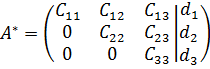
3. По ступенчатой матрице 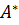восстанавливаем эквивалентную систему уравнений, которая легко решается методом подстановки.
К элементарным преобразованиям относятся:
- перестановка строк и столбцов;
- умножение всех элементов любой строки на одно и то же число;
- прибавление ко всем элементам любой строки соответствующих элементов другой строки, умноженных на одно и то же число.
Элементарные преобразования матриц приводят к эквивалентным матрицам, которые могут различаться элементами и количеством строк, то имеют обязательно одинаковые числовые характеристики. Например, эквивалентные квадратные матрицы имеют одинаковые значения определителей. Эквивалентные матрицы соединятся знаком ~
Рекомендуется:
- конкретные виды элементарных преобразований показывать в условной графической форме (см. пример ниже);
- для контроля правильности промежуточных вычислений использовать контрольный столбец;
- при перестановке столбцов учитывать, что переставляются и неизвестные в СЛАУ, восстановленной по ступенчатой матрицы.
Пример решения конкретной СЛАУ способом Гаусса (с расширенной матрицей).
Имеем неоднородную СЛАУ
1. Записываем расширенную матрицу
поз.1
2. Вводим контрольный столбец, элементы которого равны сумме элементов соответствующей строки (поз.2), затем переставляем строки и столбцы (поз.3 и 4).
поз.2 поз.3
~ 
~
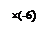поз.4 поз.5
~ 
~
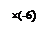
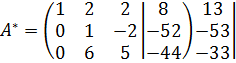поз.6
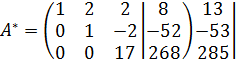
В 4ой позиции в матрице справа условно показаны операции, которые выполняются, чтобы получить нули в первом столбце (поз.5) и, затем, прийти к ступенчатой матрице (поз.6).
По ступенчатой матрице 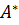(поз.6) восстанавливаем эквивалентную СЛАУ
Решаем полученную СЛАУ способом подстановки
Найденные корни совпадают с полученными другими способами, приведёнными выше.