Задачи для расчетно-графической работы

МАТЕМАТИКА

Методические рекомендации
по выполнению расчетно-графической работы по теме «Применение производной к исследованию функции» для студентов всех направлений очной формы обучения

 

Кострома
ФГБОУ ВПО Костромская ГСХА

 

Оглавление

Введение. 4

1. Введение в математический анализ. 5

1.1. Способы задания функций. 5

1.2. Способы образования функций. 6

1.3. Предельные процессы переменной x. 8

1.4. Предел функции. Бесконечно малые и бесконечно большие функции. 8

1.5. Нахождение предела функции при x ® a, x ® a – 0, x ® a + 0. 10

1.6. Раскрытие неопределенностей вида ..... 11

1.7. Нахождение пределов функций при x ® ∞, x ® – ∞, x ® + ∞.. 14

1.8. Непрерывность и разрывы функции. 15

2. Дифференциальное исчисление функций одной переменной. 20

2.1. Понятие производной. 20

2.2. Правила дифференцирования. Дифференциал функции. 21

2.3. Производные высших порядков. 24

2.4. Правило Лопиталя. 27

2.5. Уравнение касательной и нормали. 28

2.6. Исследование функций на монотонность (возрастание, убывание)
и экстремум.. 28

2.7. Нахождение наименьшего и наибольшего значений функции. 30

2.8. Исследование графиков функций на выпуклость,
вогнутость и перегиб. 32

2.9. Полное исследование функций и построение графиков. 33

3. Задания к расчетно-графической работе.………………………………………....37

4. Образец выполнения расчетно-графической работы…………………………….47

Список рекомендуемых источников. 52

Приложение. 51

Введение

Математический анализ — раздел математики, в котором, по определению Фридриха Энгельса, изучаются количественные отношения действительного мира. Математический анализ является основой высшей математики. Он охватывает те разделы математики, которые опираются на понятие функции и на идеи исчисления бесконечно малых.

Развитие математического анализа началось еще в XVI веке и продолжается до наших дней, постоянно обогащаясь новыми более совершенными методами и фактами. В разное время задачами математического анализа занимались многие великие математики. Их имена увековечены в названиях методов, теорем, признаков, правил, с которыми вы познакомитесь в процессе изучения курса математики.

Основными понятиями математического анализа являются понятия: величины, функции, предела, производной и интеграла. Изучение задач, связанных с этими понятиями, привело к образованию двух основных частей математического анализа — дифференциального и интегрального исчислений, являющихся базовыми в математической подготовке инженера.

 

1. Введение в математический анализ

Первое, с чем сталкиваются исследователи в научной и практической деятельности в разделе «Введение в математический анализ», являются величины.

Под величиной в математике понимают те свойства и качества предметов и явлений, которые можно выразить числом: длина, площадь, объем, температура, теплоемкость, цена товара, время и т.п. Нельзя отнести к величинам, например, красоту явления, характер человека и т.п.

Изучая величины, обычно абстрагируются от их конкретной природы и рассматривают только их численные значения. После чего полученные результаты становятся применимыми к величинам любой природы в различных областях человеческой деятельности: в механике, физике, инженерном деле, экономике и т.д.

Все величины подразделяют на постоянные и переменные. Постоянные величины обычно обозначают либо числами (1, 2, 3, …; 0,725; p; е, …), либо первыми буквами латинского алфавита (a, b, c, d, …). Переменные величины обычно обозначают последними буквами латинского алфавита (x, y, z, t, …). Постоянные и переменные величины можно изображать точками на числовой оси О x. При этом множество значений x,удовлетворяющих неравенству а < x < b,называют открытым интервалом и обозначают в виде(a; b). Таким образом, в сокращенной записи получим(a; b)Û { x: a < x < b }.

Аналогично определяются и понимаются множества:

[ a; b ] Û { x: a £ x £ b };

[ a; b) Û { x: a £ x < b };

[ a; +¥) Û { x: a £ x < +¥};

(–¥; a ] Û { x: –¥ < x £ a };

(–¥;+¥) = R Û { x: –¥ < x < +¥} и т.д.

 

Подробное описание этих понятий можно найти в источнике [2, § 13].

1.1. Способы задания функций

Термин функция появился впервые у Г.В. Лейбница еще в XVII веке. Обозначение функции в виде y = f (x) начал использовать Л. Эйлер в XIX веке. С понятием функции одного переменного можно ознакомиться в [2, § 14]. Мы будем рассматривать числовые функции одного переменного x: y = f (x) или y = y (x). Область определения (задания, существования) такой функции будем обозначать через D (y), а область изменения (значений) — через E (y).

Наиболее используемые способы задания функций приведем в таблице 1.

Таблица 1. Основные способы задания функций

Название способа	Чем задана функция y = y (x)	Форма задания
1. Аналитический (наиболее употребляемый)	Аналитическим выражением (формулой)	y = f (x) — явная F (x, y) = 0 — неявная — параметрическая (t — параметр)
2. Графический (наглядный, рис. 1)	Графиком (в системе координат)	Рис. 1. Графический способ
3. Табличный	Таблицей
	x	x 1	x 2	…	x n
	y	y 1	y 2	…	y n

 

 

1.2. Способы образования функций

Самыми простыми среди явно заданных функций являются 16 функций:

1) y = С — постоянная;

2) y = xⁿ — степенная (n ¹ 0);

3) y = a^x — показательная (a > 0, a ¹ 1);

4) y = log_a x — логарифмическая (a > 0, a ¹ 1);

5) y = sin x, y = cos x, y = tg x, y = ctg x, y = sec x, y = cosec x — тригонометрические;

6) y = arcsin x, y = arccos x, y = arctg x, y = arcctg x, y = arcsec x, y = arccosec x — обратныетригонометрические функции.

 

Эти функции называют основными элементарными функциями. Свойства и графики этих важных функций изучают в курсе математики средней школы. Эти сведения желательно повторить. Для этого можно использовать школьные учебники, а также [2, § 14].

Из основных элементарных функций, как из «кирпичиков», образуют множество новых функций. Для этого используют различные способы. Рассмотрим некоторые из них.

1. Образование функций с помощью арифметических операций (+, –, ×,:), например:

а) y = 3 sin x + 4 tg x – 5 lg³ x + arcsin x;

б) P_n (x) = a ₀ x ⁿ + a ₁ x ^n-1 + …+ a _n-1 x + a _n — многочлен степени n;

в) гиперболические функции:

— гиперболический синус;

— гиперболический косинус;

— гиперболический тангенс;

— гиперболический котангенс.

Заметим, что гиперболические функции получены с помощью арифметических операций из показательной функции а^x при a = e.

 

2. Образование функций с помощью повторного взятия функции:

y = f (j (x)). (1)

Такую функцию называют сложной функцией или функцией сложного аргумента. Например, сложными будут функции:

y = sin 3 x, y = arctg (lg x), y = lg (x ² + 1), (2)

а их аргументами, соответственно, 3 x,lg x, x ² + 1.

 

3. Образование функций с помощью нескольких аналитических выражений, например

(3)

Эта функция в области D (y) = [0; 3p] задана тремя различными аналитическими выражениями.

При образовании функций могут использоваться и другие, кроме перечисленных выше, операции, например, дифференцирование и интегрирование, а также бесконечное число таких операций. Из множества подобных функций выделяют наиболее простые — те, которые получены из основных элементарных функций с помощью конечного числа арифметических операций и операций взятия функций от функций и которые записаны одним аналитическим выражением. Такие функции называют элементарными. Например, элементарными будут многочлены, гиперболические функции, функции (1) и (2), а функция (3) не будет элементарной, так как она задана не одним аналитическим выражением.

1.3. Предельные процессы переменной x

При изменении переменной величины x иногда можно выделить характерную особенность в ее поведении: монотонное возрастание или убывание, неограниченное приближение к постоянному числу и т.п. Если переменная величина x (например, время) неограниченно возрастает и при этом остается положительной, то такое поведение величины x символически будем обозначать как x ® +¥. Таким образом, символическая запись x ® +¥ будет означать, что x неограниченно возрастает и в процессе изменения станет и останется больше любого сколь угодно большого числа М > 0. Итак, x ® +¥ — это один из предельных процессов поведения переменной x. Аналогично понимаются другие предельные процессы:

x ® –¥,

x ® ¥ Û | x| ® +¥,

x ® a — x неограниченно приближается к числу а,

x ® a – 0Û — x неограниченно приближается к а слева;

x ® a + 0Û — x неограниченно приближается к а справа.

1.4. Предел функции.
Бесконечно малые и бесконечно большие функции

Во всех рассмотренных ранее предельных процессах рассматривают пределы функции y = f (x). Эти пределы обозначают соответственно символами:

, , ,

, , .

Определения этих пределов даны в учебнике [2, § 16].

Предел называют пределом функции f (x) в точке а,

= f (a – 0) — пределом функции f (x) в точке а слева (левосторонним пределом),

= f (a + 0) — пределом функции f (x) в точке а справа (правосторонним пределом).

Между этими тремя пределами существует тесная связь. Выразим ее в следующей важной теореме.

Теорема (о связи между пределом функции в точке и её односторонними пределами):

Û f (a – 0) = f (a + 0), (4)

т.е. для существования предела функции в точке x = a необходимо и достаточно, чтобы существовали и были равны между собой левосторонний и правосторонний пределы функции в этой точке.

Следует помнить, что всякий предел, если он существует, — это число.

Отметим два важных случая в теории пределов.

1. Если

, (5)

то функцию a(x) называют бесконечной малой (б.м.) при x ® x ₀. Вместо формулы (5) в этом случае записывают: a(x) ® 0 при x ® x ₀. Например, функция a₁(x) = x ² – 1 будет б.м. при x ® 1, а функция a₂(x) = sin x будет б.м. при x ® 0.

Примечание 1. В определении б.м. x ₀ может быть конечным числом а, а может означать бесконечность. Так, например, функция a₃(x) = 1/ x ² будет б.м. при x ® ¥, x ® –¥, x ® +¥.

2. Если при x ® x ₀ абсолютное значение функции b(x) неограниченно возрастает, то эту функцию называют бесконечно большой (б.б.) при x ® x ₀ и записывают: или b(x) ® ¥ при x ® x ₀. Например, функция будет б.б. при x ® 1, а функция — б.б. при x ® ¥.

Примечание 2. Если в процессе x ® x ₀ b(x) ® ¥ и начиная с некоторого значения x функцияb(x) становится положительной, то пишут b(x) ® +¥ при x ® x ₀ или .

Например, .

Аналогично понимают ситуацию b(x) ® –¥ при x ® x ₀ или .

Например, .

Примечание 3. Между б.м. и б.б. функциями имеется тесная связь: в одном и том же процессе функция, обратная б.м., будет б.б., а функция, обратная б.б., — б.м. Символически эти утверждения будем записывать в виде

, (6)

. (7)

Следует иметь в виду, что в формуле (6) речь идет не о делении на ноль (такая операция, как известно, не имеет смысла), а о том, что когда знаменатель дроби стремится к нулю, а числитель нет, то дробь неограниченно возрастает. Аналогично понимается формула (7).

 

1.5. Нахождение предела функции
при x ® a, x ® a – 0, x ® a + 0

Предел функции — это число. С помощью определения предела [2, §16] это число не находят, а только убеждаются, что конкретное число является пределом. Для нахождения предела используют свойства пределов [2, §17]. Из этих свойств следует, что для отыскания предела функции в процессах x ® a, x ® a – 0, x ® a + 0 надо подставить под знак предела значение x = a. Например:

1) ;

2) ;

3) ;

4) для функции

(8)

y (2 – 0) = ,

y (2 + 0) =

В подобных ситуациях никаких сложностей не возникает. Однако иногда появляются ситуации, которые в теории пределов принято называть неопределенностями.

Так, например, при отыскании предела получаем, что P (a) = 0 и Q(a) = 0. Это означает, что при x ® a и числитель, и знаменатель одновременно стремятся к нулю. В этом случае говорят о неопределенности вида «ноль, деленный на ноль» и записывают ее символически в виде . Аналогично понимаются неопределенности вида , (0×∞), (∞ – ∞), (1^∞), (0⁰) и другие. Найти предел в такой ситуации будет означать: раскрыть указанную неопределенность.

1.6. Раскрытие неопределенностей вида

При раскрытии неопределенностей такого вида обычно используют:

1) тождественные преобразования под знаком предела;

2) замену переменной;

3) 1-й замечательный предел;

4) свойства эквивалентных б.м. функций.

 

Рассмотрим несколько типичных примеров.

 

Пример 1.

Найти предел

.

Решение

Подстановка предельного значения x = 2 под знак предела приводит к неопределенности вида . Разложим числитель и знаменатель на множители. Для разложения числителя воспользуемся правилом разложения квадратного трехчлена на множители: если дискриминант квадратного трехчлена D ³ 0, то ax ² + bx + c = a (x – x ₁)(x – x ₂), где x ₁, x ₂ — корни соответствующего квадратного уравнения. В нашем случае получаем:

x ² – 6 x + 8 = 0, D = 36 – 4×8 = 4,

Следовательно, x ² – 6 x + 8 = (x – 2) (x – 4).

Для разложения на множители знаменателя используем тождество: a ³ – b ³ = (a – b) (x ² + ab + b ²). Тогда получим

x ³ – 8 = x ³ – 2³ = (x – 2) (x ² + 2 x + 4).

Следовательно,

 

Пример 2 [1, к задачам № 61-70, п. 1].

Найти предел

.

Решение. Как и в примере 1, имеем неопределенность вида . Знаменатель легко разлагается на множители 5 x ² – 15 x = 5 x (x – 3). Разложить на множители числитель не дают находящиеся там корни. Умножим числитель и знаменатель на выражение, «сопряженное» знаменателю, и воспользуемся формулами

(a – b) (a + b) = a ² – b ², .

Тогда получим

При раскрытии неопределенностей вида тождественных алгебраических преобразований может оказаться недостаточно, особенно в пределах, содержащих тригонометрические функции. В таких ситуациях обычно используют тригонометрические тождества [1, с. 46] и первый замечательный предел. Первым замечательным пределом называют предел

. (9)

Первый замечательный предел можно переписать в символической форме

,

где в окошке ÿ может находиться любая функция.

Например, замечательными будут пределы

,

.

А вот пределы

не будут замечательными и они не обязательно равны 1.

Рассмотрим примеры, в которых используется 1-й замечательный предел.

 

Пример 3

Найти предел .

Решение

Очевидна неопределенность вида . Разделив и умножив под знаком предела на k, получим

Следовательно,

. (9.1)

Пример 4 [1, к задачам № 61-70, п. 4].

Найти предел .

 

Решение

Разделим числитель и знаменатель дроби на x, воспользуемся [2, теорема 17.9] и пределом (9.1). Тогда получим

Пример 5 [1, к задачам № 61-70, п. 4].

Найти предел .

Решение

Воспользуемся тождествами и из [1, с. 46]. Тогда получим: , .

А в соответствии с примерами 3 и 4 найдем предел

 

1.7. Нахождение пределов функций
при x ® ∞, x ® – ∞, x ® + ∞

Для отыскания предела функции в указанных предельных процессах подставлять под знаком предела вместо x бесконечность ∞ нельзя, это — символ. Для отыскания предела в таких процессах надо анализировать поведение функции, стоящей под знаком предела при соответствующем изменении переменной x.

Например: 1) (см. формулу (7)); 2) ; 3) ; 4) ; 5) ; 6)

Но, как и в процессах x ® a, x ® a – 0, x ® a + 0, здесь могут встретиться неопределенные ситуации указанных ранее видов. Рассмотрим типичный пример.

Пример 6 [1, к задачам № 61-70, п. 2].

Найти предел .

Решение

Простой анализ показывает, что при x ® ∞ числитель и знаменатель одновременно стремятся к ∞, поэтому имеем неопределенность . Разделив числитель и знаменатель на x ², получим, учитывая (7),

1.8. Непрерывность и разрывы функции

Понятие предела функции теснейшим образом связывается с другим важным понятием анализа — понятием непрерывности функции в заданной точке и на отрезке. Из двух определений непрерывности в точке приведем одно [1, § 19], которое будет использовано при решении примера из контрольной работы.

Определение 1. Функцию f (x) называют непрерывной в точке x = x ₀, если:

1) эта функция определена в точке x = x ₀ и в некоторой ее окрестности;

2) существует предел ;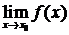

3) 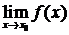= f (x ₀).

Саму точку x ₀ при этом называют точкой непрерывности функции. Точки, в которых нарушается непрерывность функции, называют точками разрыва этой функции.

Точки разрыва подразделяются на точки разрыва первого и второго рода.

Определение 2. Точку разрыва x ₀ называют точкой разрыва 1-го рода, если в ней существуют левосторонний f (x ₀ – 0) и правосторонний f (x ₀ + 0) пределы. При этом число d = f (x ₀ + 0) – f (x ₀ – 0) называют скачком функции в точке x ₀.

Определение 3. Точку разрыва x ₀ называют точкой разрыва 2-го рода, если в ней не существует или равен бесконечности по крайней мере один из односторонних f (x ₀ + 0), f (x ₀ – 0) пределов.

 

Из этих определений и свойств непрерывных функций [1, § 19.4] вытекает, что точками разрыва элементарных функций могут быть только те точки, в которых эта функция не определена, а точками разрыва неэлементарных функций, заданных несколькими аналитическими выражениями, могут быть еще и точки, в которых происходит соединение различных аналитических выражений (точки «стыка»).

 

Пример 7.

Данную функцию исследовать на непрерывность и разрывы, указать характер разрыва и изобразить ее график в окрестности точек разрыва:

.

Решение

Функция задана одним аналитическим выражением, она элементарная. Поэтому эта функция непрерывна во всех точках, где определена, т.е. в точках x ¹ 3. Данная функция не определена в одной точке: x = 3. Значит, это и будет точка разрыва. Для выяснения характера разрыва находим односторонние пределы функции:

Так как односторонние пределы равны соответственно +∞ и –∞ (т.е. не существуют), то точка x = 3 является точкой разрыва 2-го рода.

График функции изображен на рисунке 2.

Рис. 2. Вид графика функции
в окрестности точки x = 3

Пример 8.

Данную функцию исследовать на непрерывность и разрывы, указать характер разрыва и изобразить ее график в окрестности точек разрыва:

Решение

Функция определена при всех x. Она задана не одним, а двумя аналитическими выражениями, значит, является неэлементарной. И хотя эта функция определена при всех x, она может иметь разрыв в точке x = 0 (в точке «стыка»). Исследуем функцию на непрерывность в этой точке. Первое условие определения непрерывности выполнено: y (0) и D (y) = (–∞; +∞).

Найдем предел . Так как в окрестности точки x = 0 функция имеет различные формы, то найти этот предел сразу невозможно. Но тут нам поможет теорема о связи между пределом функции в точке и ее односторонними пределами согласно формулы (4).

Для этого найдем

Так как односторонние пределы существуют , и равны между собой, то существует и общий предел функции . А так как этот предел равен значению функции в точке x = 0: , то все три условия непрерывности функции в точке выполнены. А значит, x = 0 — точка непрерывности функции. Изобразим график данной функции в окрестности точки x = 0 (рис. 3).

 

Рис. 3. Вид графика функции у
в окрестности точки x = 0

Пример 9.

Данную функцию исследовать на непрерывность и разрывы, указать характер разрыва и изобразить ее график в окрестности точек разрыва:

Решение

Функция тоже не является элементарной. И хотя она определена при всех x: D (y) = (–∞, +∞), точкой разрыва может оказаться точка x = 1 (точка «стыка»). Как и в предыдущем случае, находим

y (1) ,

y (1–0) = ,

y (1+0) = .

Видно, что , значит, общий предел функции в точке x = 1 не существует. Таким образом, второе условие определения непрерывности функции в точке x = 1 не выполнено. Следовательно, x = 1 — точка разрыва. А так как односторонние пределы существуют, то точка x = 1 будет точкой разрыва 1‑го рода. Скачок функции в этой точке равен

.

Изобразим график функции в окрестности точки x = 1 (рис. 4).

 

Рис. 4. Вид графика функции у
в окрестности точки x = 1

Примечание. Функцию называют непрерывной на отрезке, если она непрерывна во всех точках этого отрезка.

Контрольные вопросы

1. Перечислите основные способы задания функции, а также их достоинства и недостатки.

2. Перечислите разновидности аналитического способа задания функции.

3. Как обозначается и находится область определения явно заданной функции?

4. Перечислите основные элементарные функции и изобразите схематично их графики.

5. Перечислите предельные процессы независимой переменной величины х.

6. Дайте определение предела функции у = f (x) при x ® + ¥ и при x ® а.

7. Какую функцию называют бесконечно малой? Приведите пример б.м. функции.

8. Какую функцию называют бесконечно большой? Приведите пример б.б. функции.

9. Как связаны межд собой б.м. и б.б. функции?

10. Назовите 1-й и 2-й замечательные пределы.

11. Дайте определение непрерывности функции в точке и на интервале.

12. Точки разрыва функции. Какими бывают разрывы функции?

13. Что такое односторонние пределы функции в точке и как они связаны с общим пределом?

2. Дифференциальное исчисление
функций одной переменной

Дифференциальное исчисление — раздел математики, в котором изучаются производные и дифференциалы функций и их применение к исследованию функций. В этом разделе рассматриваются действительные функции одного действительного переменного. Центральными понятиями дифференциального исчисления являются понятия производной и дифференциала, которые возникли еще в XVII веке в трудах английского математика И. Ньютона и немецкого — Г. Лейбница. Некоторые вопросы обоснования задач, связанных с понятием производной, были разработаны французским математиком О. Коши лишь в начале XIX века.

Дифференциальное и интегральное исчисления способствовали появлению ряда новых математических дисциплин: теории рядов, теории дифференциальных уравнений, дифференциальной геометрии, вариационного исчисления и др.

Благодаря дифференциальному и интегральному исчислениям неизмеримо расширилась область приложений математики к вопросам естествознания и техники.

2.1. Понятие производной

Понятие производной возникло из большого числа задач естествознания, приводящих к вычислению пределов одного и того же типа. Важнейшие из них — определение скорости прямолинейного движения и построение касательной к кривой. Из этих задач появилось определение производной [2, § 20.6], с помощью которого легко находятся производные простейших элементарных функций [2, § 20.2]. Рабочая таблица производных приведена в приложении.

Для обозначения производной функции y = f (x) в точке x пользуются символами:

y ¢, f ¢(x), — введены Ж. Лагранжем в 1770 г.;

— введены Г. Лейбницем в 1675 г.;

— введены И. Ньютоном в 1665 г.

Производную функции y = f (x) в точке x = x ₀обозначают

.

Примечание. Операцию отыскания производной называют дифференцированием.

 

 

2.2. Правила дифференцирования. Дифференциал функции

Сначала надо научиться пользоваться таблицей производных. Особенно это касается производных от степенной функции. Для преобразования функции к виду, приведенному в таблице производных (см. приложение), используют различные тождественные преобразования, в том числе обычные свойства степеней:

1) ;

2) ;

3) x ^m x ⁿ = x ^m+n;

4) ;

5) (x ^m)ⁿ = x ^{m n}.

 

Например:

1) ;

2) ;

3) (x ³ x ⁴)¢ = (x ⁷)¢ = 7x ⁶.

 

Далее надо научиться дифференцировать функции, образованные с помощью арифметических действий: сложения, вычитания, умножения и деления, т.е. научиться использовать формулы:

1) (u + – w)¢ = u ¢ + ¢ – w ¢;

2) (u × )¢ = u ¢ + u ¢;

3) (c× u)¢ = c u ¢, где с = const;

4)

Например:

1) (sin x + х ³ – 5)¢ = (sin x)¢ + (x ³)¢ – (5)¢ = cos x + 3 x ²;

2) (5 tg x)¢ = 5 (tg x)¢ = ;

3) (3 ln x + 4 arctg x – 6 x)¢ = (3 ln x)¢ + (4 arctg x)¢ – (6 x)¢ =

= 3 (ln x)¢ + 4 (arctg x)¢ – 6 (x)¢ =

=

4)

Для закрепления навыков желательно решить первые примеры задач № 81-90 из источника [1].

Далее отрабатываем правило дифференцирования сложной функции. Если y = f (z), где z = j (x), то

y ¢_x = y ¢ _z × z ¢_x. (10)

Это правило позволяет переписать левый столбец таблицы производных (см. прил.) для функций простого аргумента x в виде второго столбца для функций сложного аргумента z = j (x). И теперь, при нахождении производной функции, следует сразу выяснить, какой у неё аргумент. В зависимости от этого сразу определяем, какой формулой и из какого столбца таблицы надо воспользоваться. Например:

(sin x)¢ = cos x — по формуле (5) из левого столбца таблицы производных (аргументом функции является x);

(sin 5 x)¢ = cos 5 x (5 x)¢ = cos 5 x ×5 = 5 cos 5 x — по формуле (5) из правого столбца таблицы (сложным аргументом у синуса является z = 5 x);

(ln (3 x ² + 1))¢ = — по формуле (4.1) из правого столбца таблицы (сложным аргументом у логарифмической функции служит z = 3 x ² + 1);

(arctg 4 x)¢ = — по формуле (11) из правого столбца таблицы (сложным аргументом у арктангенса служит z = 4 x).

 

Полученных знаний достаточно, чтобы решить примеры 2 и 3 задач № 81-90 из источника [1].

Для решения примера 4 из названных задач отработаем правило дифференцирования неявно заданной функции [1, с. 48]. Если функция y = y (x) задана неявно, т.е. уравнением (равенством), не разрешенным относительно у, то дифференцируем данное равенство по x (с учетом того, что у есть сложный аргумент z) и из полученного уравнения находим у ¢.

 

Пример 10.

Найти производную функции, заданной равенством

6 x ³ + 4 sin y – x ³ e ^3y + 2 = 0.

Решение

Здесь функция у задана неявно. Дифференцируем данное равенство по x, и помним, что y = y (x) является функцией переменного x, а значит,ееможно считать сложным аргументом в заданном равенстве. Поэтому получаем

(6 x ³ + 4 sin y – x ⁴ e ^3y + 2)¢ = (0)¢,

18 x ² + 4 cos y×y ¢– ((x ⁴)¢ e ^3y + x ⁴(e ^3y)¢) + 0 = 0,

18 x ² + 4 cos y×y ¢– (4 x ³ e ^3y + x ⁴ e ^3y×3 y ¢) = 0,

18 x ² + 4 cos y×y ¢– 4 x ³ e ^3y – x ⁴ e ^3y×3 y ¢ = 0.

Отсюда находим:

y ¢ (4 cos y× – 3 x ⁴ e ^3y)= 4 x ³ e ^3y – 18 x ²,

 

Пример 11.

Найти производную функции, заданной равенством

5 x + 7 y ² – x ² y ³ + 10 = 0.

Решение

Действуем аналогично примеру 10

(5 x + 7 y ² – x ² y ³ + 10)¢ = (0)¢,

(5 х)¢+ (7 y ²)¢ – (x ² y ³)¢+ (10)¢ = 0,

5+ 14 y × y ¢ – (2 xy ³ + x ^2×3 y ² ×y ¢) = 0,

5+ 14 y × y ¢ – 2 xy ³ – 3 x ² y ² ×y ¢ = 0,

y ¢(14 y ×– 3 x ² y ² ×)¢ = 2 xy ³ – 5,

Остановимся еще на правиле дифференцирования параметрически заданной функции. Если функция y = y (x) задана параметрически, т.е. с помощью системы равенств

то производная находится по формуле

(11)

Пример 12. Функция задан