Задача 5. многоФАКТОРНЫЙ эксперимент
1. Линейная модель: многофакторное уравнение регрессии первого порядка:
 , (1)
, (1)
где 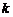 ‑ число факторов;
‑ число факторов;  ‑ текущий номер фактора,
‑ текущий номер фактора, 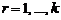 .
.
Многофакторное уравнение регрессии, также как и однофакторное строится в нормированных значениях факторов 
2. Взаимосвязь нормированных Х r и натуральных х r значений факторов:
 ,
, 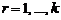 , (2)
, (2)
 ,
, 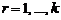 , (3)
, (3)
 ,
, 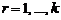 , (4)
, (4)
 ,
, 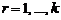 , (5)
, (5)
где  ‑ основной уровень, интервал варьирования, максимальное и минимальное значение фактора хr в натуральных значениях, соответственно. Для
‑ основной уровень, интервал варьирования, максимальное и минимальное значение фактора хr в натуральных значениях, соответственно. Для  имеем
имеем  при
при 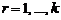 .
.
3. Матрица планирования для построения многофакторного уравнения регрессии первого порядка представляет собой таблицу, состоящую из Nk опытов с числом дублей n каждый, включает в себя столбцы: Nk, 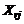 ,
,  ,
, 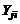 ,
, 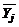 ,
, 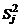 , значения которых позволяют выполнить предварительную обработку экспериментальных данных (расчёт выборочных средних и выборочных дисперсий в каждом опыте, проверка выборочных дисперсий на однородность, расчёт дисперсии воспроизводимости). Для создания такой матрицы сначаланеобходимопостроить столбец нормированных значений фактора
, значения которых позволяют выполнить предварительную обработку экспериментальных данных (расчёт выборочных средних и выборочных дисперсий в каждом опыте, проверка выборочных дисперсий на однородность, расчёт дисперсии воспроизводимости). Для создания такой матрицы сначаланеобходимопостроить столбец нормированных значений фактора 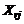
 . Для этой цели используем центральный полный факторный план (ЦПФП), который состоит из опытов полного факторного плана (ПФП) и одного опыта в центре плана (0, 0, …, 0). Число опытов ПФП при варьировании каждого фактора на 2-х уровнях
. Для этой цели используем центральный полный факторный план (ЦПФП), который состоит из опытов полного факторного плана (ПФП) и одного опыта в центре плана (0, 0, …, 0). Число опытов ПФП при варьировании каждого фактора на 2-х уровнях  равно
равно  . Количество опытов ЦПФП равно
. Количество опытов ЦПФП равно  .
.
4. Предварительная обработка экспериментальных данных матрицы планирования с числом опытов 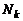 (
( ) и числом дублей в каждом опыте n (
) и числом дублей в каждом опыте n ( ).
).
4.1. Выборочное среднее  в каждом опыте:
в каждом опыте:
 ,
,  . (6)
. (6)
4.2. Выборочная дисперсия 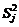 в каждом опыте:
в каждом опыте:
 ,
,  . (7)
. (7)
4.3. Проверка всех 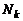 выборочных дисперсий на однородность по критерию Кохрена:
выборочных дисперсий на однородность по критерию Кохрена:
‑ экспериментальное значение критерия Кохрена  .
.
 ; (8)
; (8)
‑ табличное значение критерия Кохрена  при числах степеней свободы
при числах степеней свободы  ,
,  и доверительной вероятности р выбирается из таблицы Приложения 5;
и доверительной вероятности р выбирается из таблицы Приложения 5;
‑ выборочные дисперсии  с доверительной вероятностью р однородны, если
с доверительной вероятностью р однородны, если
 , (9)
, (9)
‑ выборочные дисперсии  с доверительной вероятностью р неоднородны, если
с доверительной вероятностью р неоднородны, если
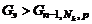 . (10)
. (10)
Если выборочные дисперсии неоднородны, необходимо переделать опыт, в котором выборочная дисперсия наибольшая.
4.4. Если все выборочные дисперсии по критерию Кохрена однородны, то дисперсия воспроизводимости  и её число степеней свободы
и её число степеней свободы  рассчитывают по формулам:
рассчитывают по формулам:
 , (11)
, (11)
 . (12)
. (12)
5. Матрица моделирования на базе матрицы планирования для построения многофакторного уравнения регрессии первого порядка представляет собой таблицу, которая строится из 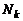 опытов с числом дублей n каждый, включает в себя столбцы: Nk,
опытов с числом дублей n каждый, включает в себя столбцы: Nk,  ,
, 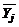 ,
, 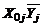 ,
,  ,
,  ,
, 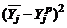 , значения которых позволяют провести окончательную обработку экспериментальных данных (расчёт коэффициентов уравнения регрессии и их доверительные интервалы, проверка уравнения регрессии на адекватность, расчёт абсолютной погрешности в случае адекватности уравнения регрессии).
, значения которых позволяют провести окончательную обработку экспериментальных данных (расчёт коэффициентов уравнения регрессии и их доверительные интервалы, проверка уравнения регрессии на адекватность, расчёт абсолютной погрешности в случае адекватности уравнения регрессии).
Столбец нормированного фактора  состоит из элементов
состоит из элементов  . Нормированные значения фактора
. Нормированные значения фактора  для плана ЦПФП равны
для плана ЦПФП равны  и для опыта в центре плана (0, 0, …, 0).
и для опыта в центре плана (0, 0, …, 0).
Отметим важное свойство матрицы моделирования: все её факторы  взаимно ортогональны, так как
взаимно ортогональны, так как  и
и  (
( ). Ортогональность факторов матрицы моделирования позволяет определить коэффициенты уравнения регрессии, а также их доверительные интервалы, независимо друг от друга по относительно простым формулам.
). Ортогональность факторов матрицы моделирования позволяет определить коэффициенты уравнения регрессии, а также их доверительные интервалы, независимо друг от друга по относительно простым формулам.
5.1. Коэффициенты многофакторного уравнения регрессии первого порядка  для ЦПФП, при условии, что факторы Х 0,, Х 1, Х 2 ортогональны, рассчитывают по формулам:
для ЦПФП, при условии, что факторы Х 0,, Х 1, Х 2 ортогональны, рассчитывают по формулам:
 , (13)
, (13)
 ,
,  , (14)
, (14)
причём для ЦПФП:  , (15)
, (15)
 ,
,  (16)
(16)
5.2. Проверка коэффициентов многофакторного уравнения регрессии первого порядка на значимость.
Дисперсии значимости коэффициентов многофакторного уравнении регрессии первого порядка для ЦПФЭ при условии, что факторы Х 0,, Х 1, Х 2 ортогональны, рассчитывают по формулам:
 , (17)
, (17)
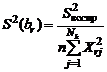 ,
,  . (18)
. (18)
Так как  , то для коэффициентов
, то для коэффициентов  выполняется равенство:
выполняется равенство:
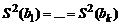 , (19)
, (19)
Доверительные интервалы коэффициентов многофакторного уравнения регрессии первого порядка рассчитываются по критерию Стьюдента:
 , (20)
, (20)
 ,
,  , (21)
, (21)
где  ‑ табличное значение критерия Стьюдента при числе степеней свободы
‑ табличное значение критерия Стьюдента при числе степеней свободы  и доверительной вероятности р выбирается из таблицы Приложения 2.
и доверительной вероятности р выбирается из таблицы Приложения 2.
Так как выполняется уравнение (19), то и доверительные интервалы линейных коэффициентов равны:
 ,
,  . (22)
. (22)
Коэффициенты многофакторного уравнения регрессии первого порядка значимы, если выполняются следующие неравенства:
 ,
,  . (23)
. (23)
Если для какого-либо коэффициента указанное неравенство не выполняется, то этот коэффициент незначим, и его необходимо исключить из уравнения регрессии.
5.3. Проверка многофакторного уравнения регрессии первого порядка на адекватность.
Дисперсия адекватности  и её число степеней свободы
и её число степеней свободы  равны:
равны:
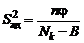 , (24)
, (24)
 , (25)
, (25)
где n – число дублей в каждом опыте;  ‑ остаточная сумма квадратов;
‑ остаточная сумма квадратов; 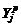 ‑ расчетные значения параметра Y, полученные по многофакторному уравнению регрессии первого порядка
‑ расчетные значения параметра Y, полученные по многофакторному уравнению регрессии первого порядка  (
( ), которое содержит только значимые коэффициенты; Nk ‑ число опытов; В ‑ число значимых коэффициентов многофакторного уравнения регрессии первого порядка.
), которое содержит только значимые коэффициенты; Nk ‑ число опытов; В ‑ число значимых коэффициентов многофакторного уравнения регрессии первого порядка.
Адекватность уравнения регрессии проверяется по критерию Фишера:
‑ экспериментальное значение критерия Фишера F э, (отношение большей дисперсии к меньшей):
 , (26)
, (26)
‑ табличное значение критерия Фишера  , где
, где  ‑ число степеней свободы большей дисперсии,
‑ число степеней свободы большей дисперсии,  ‑ число степеней свободы меньшей дисперсии, выбирается из таблицы Приложения 4;
‑ число степеней свободы меньшей дисперсии, выбирается из таблицы Приложения 4;
‑ уравнение регрессии с доверительной вероятностью р адекватно, если:
 , (27)
, (27)
‑ уравнение регрессии с доверительной вероятностью р неадекватно, если:
 . (28)
. (28)
6. Абсолютная погрешность  параметра
параметра  рассчитанного по уравнению
рассчитанного по уравнению  , в случае его адекватности, определяется по формуле:
, в случае его адекватности, определяется по формуле:
 , (29)
, (29)
где  ‑ табличное значение критерия Стьюдента при числе степеней свободы
‑ табличное значение критерия Стьюдента при числе степеней свободы  и доверительной вероятности р находится из таблицы Приложения 2.
и доверительной вероятности р находится из таблицы Приложения 2.
7. Если полученное многофакторное уравнение регрессии первого порядка неадекватно, следует перейти к построению многофакторного уравнению регрессии второго порядка.