При изучении кинематических и динамических свойств плоских механизмов удобно заменять механизм с высшими кинематическими парами 4-го класса механизмом с низшими кинематическими парами.
Эквивалент высшей пары в плоском механизме можно найти путем сопоставления двух механизмов, у которых одно и то же число степеней свободы и одинаковые законы движения звеньев.
Пусть в исходном механизме имеется одна высшая пара, в заменяющем – лишь пары 5-го класса.
Приравнивая выражения для W обоих механизмов, вычисленные по формуле (1.2), можно получить
3 n – 2 р 5 – р 4 = 3 n / – 2 р 5/.
Штрихи относятся к заменяющему механизму, отсюда
р 4 = 2(р 5/ – р 5) – 3(n / – n). (1.6)
Равенство (1.6) превращается в тождество при p 4 = 1; p 5/ – p 5 = 2
и n / – n = 1, т.е. заменяющий механизм по сравнению с исходным должен содержать одно дополнительное звено и две кинематические пары 5-го класса.

Рис. 1.10. Замена высшей пары одним звеном и двумя низшими парами:
а – замена высшей пары, образованной двумя криволинейными поверхностями;
б – замена высшей пары, образованной криволинейной поверхностью и прямой линией; в – замена высшей пары, образованной криволинейной поверхностью
и точкой, образованной двумя прямыми линиями
Чтобы звенья заменяющего механизма в рассматриваемом положении совершали такое же движение, как и звенья исходного механизма, необходимо соблюдать определенные правила замены высшей пары одним звеном и двумя низшими парами (рис. 1.10).
Избыточные связи
В некоторых случаях подсчитанное по формуле (1.1) или (1.2) число степеней свободы механизма оказывается меньше 1, но при соблюдении определенных условий сборки механизм обладает положительной подвижностью. Это свидетельствует о наличии в механизме избыточных связей, которые не влияют на движение звеньев и которые не учитывают при определении числа степеней свободы механизма.
Так, если число избыточных связей в механизме q, то число степеней свободы механизма с избыточными связями
W = 6 n – 5 p 5 – 4 p 4 – 3 p 3 – 2 p 2 – p 1 + q. (1.7)
Например, в механизме сдвоенного параллелограмма (рис. 1.11) подсчитанное по формуле (1.2) число степеней свободы
W = 3∙4–2∙6 = 0.
Однако если AD // EF // BC и оси шарниров строго параллельны, то наличие звена 4 не вносит геометрических связей и число степеней свободы механизма равно 1, как и в механизме без звена 4 (рис. 1.12). Звено 4 устанавливают для исключения превращения параллелограмма

| 
|
| Рис. 1.11. Механизм сдвоенного параллелограмма | Рис. 1.12. Шарнирный четырехзвенник |
в антипараллелограмм при выходе из положений, в которых оси всех звеньев расположены на одной прямой.
При несоблюдении указанных геометрических соотношений число степеней свободы механизма действительно равно нулю и движение звеньев невозможно.
Согласно формуле (1.2), в шарнирном четырехзвеннике (см. рис. 1.12) W = 1. Но если обусловленная неточностью изготовления непараллельность осей вращательных пар механизма не может быть компенсирована зазорами между элементами этих пар, то его следует рассматривать как пространственный механизм. И тогда, согласно (1.7), число избыточных связей в этом механизме составит
q = 1–6∙3+5∙4 = 3.
Сборка такого механизма возможна за счет деформации звеньев, а при его работе происходит усиленное изнашивание пар трения, появляется возможность заклинивания элементов кинематических пар.
Изменением подвижности кинематических пар можно устранить имеющиеся в механизме избыточные связи. Так, если в рассматриваемом шарнирном четырехзвеннике одну вращательную пару заменить сферической, а другую – сферической с пальцем либо одну вращательную пару заменить сферической, а другую – цилиндрической, то такие механизмы будут лишены избыточных связей. Для них
q = 1–6∙3+5∙2+4∙1+3∙1 = 0.
Для кривошипно-ползунного механизма (см. рис. 1.2, б) устранить избыточные связи можно, например, заменой вращательной пары «кривошип – шатун» сферической, а поступательной – цилиндрической. Возможны и другие варианты устранения избыточных связей в рассмотренных механизмах.
Механизм без избыточных связей можно собрать без натягов при любых неточностях изготовления, что уменьшает силы трения в кинематических парах и увеличивает срок службы и надежность механизма. Такой механизм легко приспосабливается к деформации основания.
1.6. Алгоритм проведения структурного анализа
плоского механизма
1. Составить структурную схему механизма.
2. Определить степень подвижности механизма по формуле (1.2).
3. Заменить высшие пары низшими и определить число степеней свободы заменяющего механизма по формуле (1.2).
4. Разложить механизм на структурные группы. Разложение следует начинать с отсоединения простейшей группы Ассура, наиболее удаленной по кинематической цепи от входного звена. При этом число степеней свободы оставшейся кинематической цепи должно соответствовать числу степеней свободы исходного механизма. Если отсоединить структурную группу 2-го класса не удается, следует отсоединить группу 3-го класса и т.д. После отсоединения первой группы отсоединяют следующую группу и т.д.
В результате разложения остается одно входное звено со стойкой, если степень подвижности механизма равна единице. Если число степеней свободы механизма равно k, то должно остаться k входных звеньев.
5. Записать формулу строения механизма, показывающую, в какой последовательности и какие группы Ассура присоединены к механизму 1-го класса.
6. Определить класс и порядок всего механизма.
Приведем пример определения порядка структурного анализа плоского механизма, представляющего замкнутую кинематическую цепь (рис. 1.13).

Рис. 1.13. Плоский механизм замкнутой кинематической цепи:
A, B, C, D, E, E’, G, G’, F – кинематические пары
1. Определим число степеней свободы механизма по формуле (1.2):
W = 3 n – 2 p 5 – p 4.
Для данного механизма n = 6, p 5 = 7, p 4 = 2. В случае соединения нескольких звеньев (например, шарнир E) число кинематических пар определяется числом соединяемых звеньев, уменьшенным на единицу.
Так, в шарнире Е соединяются три звена, следовательно, число кинематических пар здесь p 5 = 2.
Таким образом,
W = 3·6–2·7–2 = 2.
Формально это говорит о том, что для определенности движения всех звеньев механизма в нем должно быть два входных звена или одно входное звено с двумя заданными независимыми движениями.
Однако все звенья механизма совершают вполне определенное движение лишь при одном заданном движении одному из них (например, кулачку 1). Лишнее число степеней свободы механизма, получаемое при подсчете по формуле (1.2), обусловлено наличием ролика 2. Возможность вращения ролика 2 относительно стержня 3 не влияет на движение остальных звеньев механизма.
Если жестко закрепить ролик 2 на стержне 3, то при этом относительное движение остальных звеньев останется прежним, но число подвижных звеньев n и число кинематических пар 5-го класса p 5 уменьшится на единицу (n = 5, p 5 = 6), а число степеней свободы механизма окажется равным
W = 3×5–2×6–2 = 1.
2. Производим замену высших кинематических пар B и D механизма эквивалентными кинематическими цепями с низшими парами в соответствии со схемами, приведенными на рис. 1.14.

Рис. 1.14. Структурная схема заменяющего механизма
| На рис. 1.14 приведена схема заменяющего механизма. Число степеней свободы этого механизма W = 3×7–2×10 = 1. 3. Разложим механизм на структурные группы. Разложение начинаем с отсоединения простейшей группы Ассура, наиболее удаленной по кинематической цепи от входного звена. Это группа 2-го класса 2-го вида, |  Рис. 1.15. Структурная группа 2-го класса 2-го порядка
Рис. 1.15. Структурная группа 2-го класса 2-го порядка
|
содержащая звенья 5 и 6 (рис. 1.15). Оставшаяся кинематическая цепь является замкнутой, ее степень подвижности W = 3×5–2×7 = 1, т.е. осталась прежней. Значит, отсоединение выполнено правильно.
Дальнейшее отсоединение простейших групп невозможно. Так, отсоединение звеньев 3 и 4 или 3 и 7 приведет к размыканию кинематической цепи.
Если не удается отсоединить группу 2-го класса, пытаются отсоединить группу 3-го или 4-го классов, состоящую из четырех звеньев и шести кинематических пар. Так, звенья 2, 3, 4 и 7 образуют структурную группу 3-го класса 3-го порядка (рис. 1.16).
В результате разложения остался механизм 1-го класса (входное звено со стойкой), имеющий W = I (рис. 1.17). Формула строения механизма записывается в порядке присоединения структурных групп к ведущему звену:  .
.
Таким образом, данный механизм есть механизм 3-го класса 3-го порядка. Он образован последовательным присоединением к входному звену и стойке структурных групп 3-го класса 3-го порядка и 2-го класса 2-го порядка второго вида.

|

|
| Рис. 1.16. Структурная группа 3-го класса 3-го порядка | Рис. 1.17. Механизм 1-го класса |
1.6.1. Примеры решения задач по структурному анализу
Пример1.

|
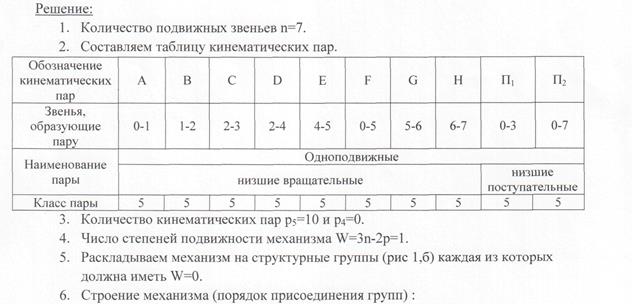
На рисунке показана схема механизма автомата-перекоса вертолета. Ведущее звено АВ отмечено круговой стрелкой.
Решение. 1) Подсчитывается степень подвижности механизма по формуле Чебышева. Для этого определяются общее число звеньев к=8, число подвижных звеньев n=к-1=7, число кинематических пар V класса p5=10 (кинематических пар IV класса нет, поэтому нет необходимости в построении заменяющего механизма). В механизме отсутствуют пассивные связи и звенья, вносящие лишние степени свободы. Степень подвижности ω равна
ω = Зn - 2р5 - р4 = 3 • 7 - 2 • 10 - 0 = 1.
2) Ведущее звено задано в условии примера, и оно должно быть одно, так как ω = 1.
3) Механизм расчленяется на группы Ассура. Вначале отделяется группа Ассура второго класса, образованная звеньями 7 и 6 (LKG), а затем группа второго класса, состоящая из звеньев 5 и 4 (HEF), и, наконец, группа второго класса, составленная звеньями 3 и 2 (DCB).
На этом расчленение механизма заканчивается, так как остались ведущее звено 1 и стойка 8 (на рисунке отделяемые группы обведены замкнутыми контурами).
4) Записывается формула строения механизма:
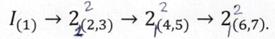
В этой формуле римская цифра I обозначает ведущее звено, арабские -классы присоединяемых групп (2), а индексы при арабских цифрах указывают, какие звенья образовали ведущее звено и присоединяемые группы.
Из формулы строения механизма видно, что наивысший класс присоединенных групп - второй, поэтому механизм автомата-перекоса вертолета при ведущем звене 1 следует отнести ко второму классу.

|

|

|

|
1.6.2 Задачи по структурному анализу
Задачи 1 – 8.
 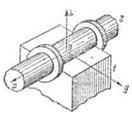
|
Определить класс кинематической пары образованной звеньями 1 и 2.

|
Задача 1. Задача 3. Задача 4.



Задача 4.
Задача 2.
Задача 6.

|

|
Задача 8.
Задача 7.
| З |
Определить степень подвижнасти № 9 – 20



Задача №9.
Задача №10. Задача №11.


Задача № 12. Задача № 13-14.
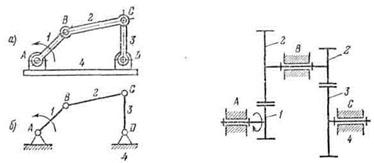

Задача № 15-16. Задача № 17 Задача №18

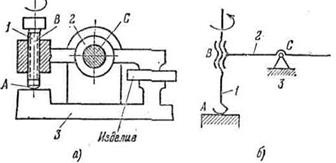
Задача № 19 Задача № 20-21

|

|
Выполнить структурный анализ механизма №22-39
Задача № 22 Задача № 23
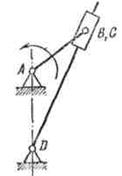
|

|

|
Задача № 24 Задача № 25 Задача № 26

|

|

|
Задача № 27 Задача № 28 Задача № 29
  
|
Задача № 30 Задача № 31 Задача № 32
 |

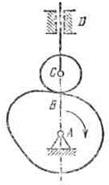

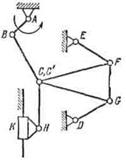
Задача № 33 Задача № 34 Задача № 35 Задача № 36
 | |||||
 | |||||
 | |||||
Задача № 37 Задача №38 Задача № 39