Решение
Способ (традиционный)
Рассмотрим два случая
Подумайте, почему именно два и именно таких
1.  при этом
при этом 
Отсюда  при условии
при условии 
Значит, в этом случае  при
при 
2. 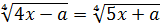 при условии
при условии 
Тогда  при условии
при условии 
Значит,  при условии
при условии 

Таким образом, в этом случае  при
при 

Значит, корень 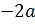 лежит на данном отрезке при
лежит на данном отрезке при 
Если корни совпадают, то 
Значит, исходное уравнение будет иметь ровно один корень на отрезке  при
при 
Ответ: 
Способ (графический)
Изобразим на плоскости  следующие условия
следующие условия
1. 
2. 
3. 
4. 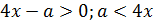
5. 
6. 

Отсюда видно, что уравнение имеет единственное решение на отрезке  при
при 
Попробуйте объяснить, как из полученного чертежа следует такой ответ
Ответ: 
2. Решить систему для всех значений параметра

Решение
Способ (метод подстановки)

Если 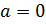 , то система имеет вид
, то система имеет вид 
Если  , то
, то 
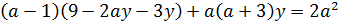

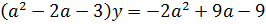
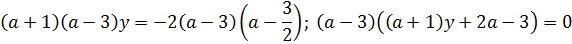
Замечание: попробуйте пройти таким путем, выражая переменную 
Если  , то полученное равенство всегда верно
, то полученное равенство всегда верно
При  система принимает вид
система принимает вид 
Значит, при  система имеет бесконечно много решений вида
система имеет бесконечно много решений вида  , где
, где  – произвольное число.
– произвольное число.
Если  , то
, то 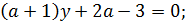
Если  , то
, то  , система решений не имеет.
, система решений не имеет.
Если  , то
, то 
Тогда 
Обратим внимание на то, что при подстановке 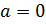 в полученные выражения для переменных, получим пару
в полученные выражения для переменных, получим пару  , как и было получено в начале решения.
, как и было получено в начале решения.
Таким образом, получаем: при  система имеет бесконечно много решений вида
система имеет бесконечно много решений вида  , где
, где  – произвольное число; при
– произвольное число; при  система решений не имеет; при
система решений не имеет; при  система имеет единственное решение вида
система имеет единственное решение вида 
Способ (метод сложения-вычитания)
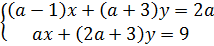
Если 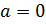 аналогично способу 1 получим пару
аналогично способу 1 получим пару 
Если  система принимает вид
система принимает вид 
Если  , домножим первое уравнение на
, домножим первое уравнение на  , а второе на
, а второе на 

Вычтем из первого уравнения второе


Далее, рассуждая как в способе 1 получим, что при  система имеет бесконечно много решений вида
система имеет бесконечно много решений вида  , где
, где  – произвольное число, а при
– произвольное число, а при  получим
получим  . И далее, снова как в способе 1 получим, что при
. И далее, снова как в способе 1 получим, что при  система решений не имеет, а если
система решений не имеет, а если  ,
,
то 
Замечание: с этого момента можно действовать, как в способе 1 – подставить найденное значение в любое из уравнений системы
Далее, если  , то
, то 
Если  , то
, то 
Если  , домножим первое уравнение на
, домножим первое уравнение на  , а второе на
, а второе на 

Вычтем из первого уравнения второе

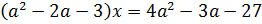


При  получаем бесконечно много решений
получаем бесконечно много решений
При  система решений не имеет
система решений не имеет
При 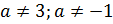 получаем, что
получаем, что 
Снова, как и в способе 1 можно обратить внимание, что полученные формулы для переменных работают и в случае 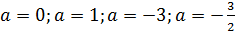
Таким образом, получаем: при  система имеет бесконечно много решений вида
система имеет бесконечно много решений вида  , где
, где  – произвольное число; при
– произвольное число; при  система решений не имеет; при
система решений не имеет; при  система имеет единственное решение вида
система имеет единственное решение вида 
Способ (определители)
Замечание: способ подходит для тех, кто хоть немного помнит, что такое матрицы 2х2 и их определители
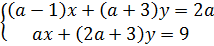
Рассмотрим матричную запись системы

Вычислим определитель системы




Тогда, если 

Если  – система решений не имеет
– система решений не имеет
Если  – система имеет бесконечно много решений
– система имеет бесконечно много решений
Подумайте, почему при  сделаны именно такие выводы о количестве решений системы
сделаны именно такие выводы о количестве решений системы
Подставим  в систему, получим
в систему, получим 
Также, как в способе 1, получаем, что система имеет бесконечно много решений вида  , где
, где  – произвольное число.
– произвольное число.
Таким образом, получаем: при  система имеет бесконечно много решений вида
система имеет бесконечно много решений вида  , где
, где  – произвольное число; при
– произвольное число; при  система решений не имеет; при
система решений не имеет; при  система имеет единственное решение вида
система имеет единственное решение вида 
Задачи для самостоятельного решения
1. Решить систему для всех значений параметра

2. Найдите все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение  имеет ровно одно решение на отрезке
имеет ровно одно решение на отрезке 