Основы вариационного исчисления

Теория оптимального управления

 

Литература

1. Эльсгольц «Вариационное исчисление».

2. Сиразетдинов Т.К. «Оптимизационные задачи авиационной техники».

3. Сиразетдинов Т.К. «Основы теории оптимальных процессов».

4. Дегтярев Г.Л., Семенов П.К. «Оптимальное управление стохастическими системами при неполной информации».

5. Брайсон, Хо-Ю-ШИ «Прикладная теория оптимального управления».

6. Дегтярев Г.Л., Ризаев И.С. «Синтез локально-оптимальных алгоритмов управления ЛА».

7. Ройтенберг Я.И. Автоматическое управление.

 

1. Математическая постановка задач оптимального управления.

Предположим, что управляемый процесс описывается совокупностью дифференциальных уравнений

(1.1)

с начальными условиями

(1.2)

Здесь: 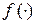- n - мерная функция своих аргументов,

- n - мерный вектор, характеризующий состояние управляемого процесса в момент времени ,

- r - мерный вектор управляющих воздействий (из некоторого заданного класса функций), - время,

- начальное состояние.

Если управление на отрезке , где - конечное время управления, задано , можно построить соответствующее ему решение системы (1.1), (1.2) .

Другому управлению будет соответствовать другая траектория .

Как известно, задача синтеза управления заключается в построении таких управляющих воздействий, при которых выполняется совокупность ограничений на состояние процесса, например, по времени переходного процесса, по величине максимального перерегулирования и т.п.

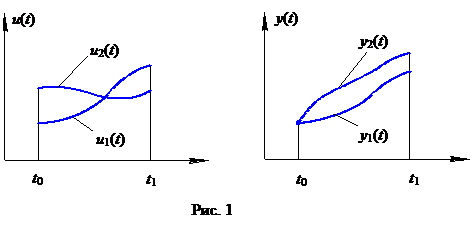
Задача же оптимального управления заключается в отыскании таких управляющих воздействий, при которых управляемый процесс будет наилучшим в некотором смысле. При этом для оценки качества управляемого движения вводится функционал .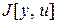

Понятие функционала

Известно, что если каждому значению переменной соответствует определенное значение переменной , то говорят, что задана функция .

Если каждой функции можно поставить в соответствие некоторое числовое значение переменной , то говорят, что задан функционал на множестве реализаций функции . Таким образом, областью определения функционала является множество функций.

Примерами функционала может быть длина кривой , соединяющей две точк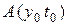и и на плоскости

,

или площадь 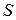, ограниченная кривой

.

В качестве функционала может быть расход топлива, необходимый для перелета самолета из пункта в пункт . Величина этого расхода будет зависеть от выбранной траектории полета.

В качестве функционала может рассматриваться значение функции в некоторой точке , т.е.

.

В качестве такой точки может быть конечная точка 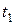, т.е. или некоторая функция конечного состояния, т.е.

.

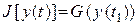Различают следующие виды функционалов.

1) Функционал Лагранжа

, (1.3)

где - некоторая достаточно-гладкая функция своих аргументов, свойства которой оговариваются в конкретном случае.

2) Функционал Майера

(1.4)

 

3) Функционал Больца

(1.5)

В смысловом плане эти функционалы различаются, но с точки зрения математической принципиальной разницы нет, т.к. от одной формы представления функционала можно перейти к другой.

Например, путем введения переменной

функционал Лагранжа

можно представить в форме Майера

,

где и связаны уравнением

.

4) Локальный функционал. Рассмотренные функционалы характеризуют качество управляемого процесса на конечном (или бесконечном) интервале времени. Однако часто бывает необходимо, чтобы поведение системы было оптимальным в некотором смысле в любой текущий момент времени. К таким требованиям относится, например, требование максимальной текущей точности функционирования системы. В этом случае критерием оптимальности служит некоторый функционал (функция) , параметрически зависящий от времени , определенный на множестве функций и . Общий вид такого функционала можно представить в следующем виде

(1.6)

Управление , минимизирующее в текущий момент времени, называется локально-оптимальным.

Теперь задача оптимального управления может быть сформулирована как задача поиска такой управляющей функции и соответствующей траектории , удовлетворяющей системе (1.1), (1.2), на которых некоторый функционал 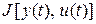достигает минимального или максимального значения.

При этом каждый раз оговаривается класс функций, среди которых отыскивается минимум или максимум (класс функций сравнения).

Это может быть класс непрерывных, кусочно-непрерывных или непрерывно-дифференцируемых определенное число раз функций. Свойства любого функционала существенно зависят от того, на каком классе функций он задан.

В том случае, когда функция - не зависит от времени (постоянна), функционал становится функцией этого параметра и задача оптимизации сводится к задаче минимизации (максимизации) функции.

 

Пример 1. Понятие оптимальной ширины полосы пропускания системы.

Рассмотрим систему, где

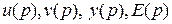- изображения

(по Лапласу) задающего воздействия , помехи , выходной переменной и ошибки системы , соответственно,

- передаточная функция разомкнутой системы.

Учитывая, что , где - передаточная функция замкнутой системы, получим

.

Предположим, что и - независимые стационарные случайные процессы с известными спектральными плотностями (плотностями распределения дисперсии по частотам) . Тогда спектральная плотность ошибки системы

, где - частотная функция замкнутой системы.

Пусть ,

т.е. АЧХ системы .

Здесь - характеризует ширину полосы пропускания системы.

Тогда дисперсия ошибки

при заданных является функцией , причем, с увеличением уменьшается, а увеличивается, т.е. с увеличением лучше отрабатывается полезный сигнал, но увеличивается влияние помехи. Поэтому может быть поставлена задача определения такой , при которой дисперсия ошибки является минимальной. Используя необходимые условия экстремума

,

получим уравнение, которому с необходимостью удовлетворяет искомая оптимальная ширина полосы пропускания системы

. (1.7)

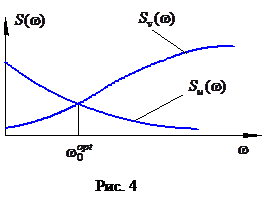Последнее может быть решено графически.

Так как уравнение (1.7) – нелинейное, оно может иметь несколько решений, каждое из которых должно быть дополнительно исследовано и найдено действительно оптимальное.

 

Методы решения задач оптимального управления

Теоретической основой решения задач оптимального управления являются:

1) вариационное исчисление,

2) принцип максимума Понтрягина,

3) метод динамического программирования Беллмана.

В том случае, когда задача оптимального управления сводится к параметрической оптимизации для поиска оптимальных параметров, используются методы минимизации функций.

 

Основы вариационного исчисления

2.1. Вводные замечания.

В вариационном исчислении нет деления функций на управляющие и функции состояния. Вводится семейство функций из определенного класса. Это могут быть кусочно-непрерывные, непрерывные, непрерывно-дифференцируемые конечное число раз функции, определенные на отрезке . На множестве этих функций определяется функционал .

Для определенности будем предполагать, что функционал задан в форме Лагранжа, а подынтегральная функция содержит, кроме функций , и их производные, т.е. .

Функция доставляет минимум функционалу , если для любой другой функции выполняется неравенство

.

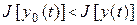Если выполняются неравенство противоположного знака, доставляет максимум функционалу .

Функция , доставляющая минимум или максимум (экстремум) функционалу , называется экстремалью.

Следует отметить, что минимум или максимум функционала может отыскивается среди всех кривых сравнения из некоторой области или среди, так называемых, близких кривых сравнения.

Если минимум (максимум) достигается среди близких кривых сравнения, он называется относительным. Если же он отыскивается среди всех кривых сравнения, то – абсолютным. При этом мера близости для разных классов функций сравнения задается по-разному.

Мерой близости двух непрерывных или кусочно-непрерывных кривых и на отрезке может быть величина

(1.7)

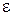Такая мера называется расстоянием нулевого порядка. Если , где - достаточное малое положительное число, то говорят, что находится в 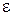- окрестности функции . Расстоянием первого порядка между двумя непрерывно-дифференцируемыми функциями и на отрезке называется величина

(1.8)

Понятно, что из близости функций по мере следует их близость и по мере 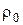. Обратное же не имеет место.

Если 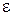- окрестность определяется мерой , то говорят о сильной 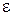- окрестности, если же – мерой - слабой 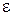- окрестности.

Аналогично могут быть введенные понятия расстояний более высокого порядка.

 

2.2. Необходимое условие относительного экстремума.

Обозначим через искомую экстремаль. Тогда любую другую функцию из рассматриваемого класса можно представить в виде , где - вариация функции. При этом, если является малой в смысле некоторой меры, то говорят о близких кривых сравнения.

Понятно, что

,

тогда условия

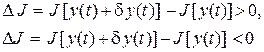(1.9)

будут необходимыми и достаточными условиями минимума и максимума, соответственно.

Однако, эти условия не конструктивны. Для получения более эффективных условий вводится понятие первой вариации функционала. Для этого представим приращение функционала в виде

, (1.10)

где 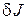- линейная относительно часть приращения, содержит величины более высокого порядка малости, чем , т.е. при .

Тогда при достаточно малых знак приращения будет определяться знаком первой вариации .

Из выражения (1.10) следует, что необходимым условием минимума или максимума (экстремума) функционала является условие

(1.11)

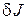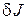Для доказательства предположим, что кривая доставляет минимум (максимум) функционалу . Это означает, что при любых . Если теперь предположить, что условие (1.11) неверно, то в силу линейности от первая вариация , а значит и будут менять знак при смене знака , что противоречит условию и доказывает справедливость условия (1.11).

Условие (1.11) еще называют условием стационарности. Поскольку оно является необходимым условием экстремума, ему должны удовлетворять все кривые, доставляющие и минимум, и максимум функционалу , т.е. это условие позволяет выделить все множество функций, среди которых находится и искомое, если оно существует. Используя условие (1.11), можно получить уравнения, которым с необходимостью должны удовлетворять искомые экстремали.

 

2.3. Основная лемма вариационного исчисления.

Лемма. Пусть - заданная непрерывная функция, удовлетворяющая уравнению

, (1.12)

где - любая непрерывная функция, то .

Доказательство. Предположим, что условие не выполняется и существует некоторая точка , в которой . Для определенности положим, что . Тогда в силу непрерывности функции существует в окрестности точки некоторый интервал 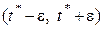, где .

Поскольку - любая непрерывная функция, выберем ее следующим образом

В этом случае

,

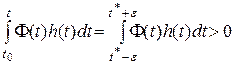что противоречит условию (1.12) и доказывает лемму.

2.4. Простейшая задача вариационного исчисления, уравнение Эйлера.

Рассмотрим простейшую задачу вариационного исчисления. Среди непрерывно-дифференцируемых скалярных функций сравнения , удовлетворяющих условиям (проходящих через точки 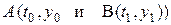, найти такую, которая доставляет минимум функционалу

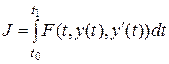, (1.13)

где - достаточно гладкая

функция своих аргументов.

Для решения задачи используем условие (1.11). Для этого приращение функционала (1.13)

,

воспользовавшись формулой Тейлора, представим в следующим виде

. (1.14)

где - содержит величины более высокого порядка малости, чем и .

И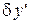з выражения (1.14) следует, что

(1.15)

Поскольку решение мы ищем в классе непрерывно-дифференцируемых функций, то и вариации тоже будет непрерывно-дифференцируемыми. Нетрудно показать, что справедливо равенство

. (1.16)

Учитывая (1.16), представим

. (1.17)

Тогда, подставляя (1.17) в (1.15) и интегрируя, получим

.

Так как все функции сравнения проходят через заданные точки , то и

.

Теперь в силу произвольности из условия , применяя основную лемму вариационного исчисления, получим уравнение экстремали

, (1.18)

которое называется уравнением Эйлера.

Уравнению Эйлера удовлетворяют кривые, доставляющие как относительный минимум, так и относительный максимум функционалу (1.13), поэтому для идентификации экстремума необходимы дополнительные исследования.

Учитывая, что , уравнение Эйлера можно представить в виде

.

То есть уравнение Эйлера – это дифференциальное уравнение второго порядка относительно , его общее решение содержит две произвольные постоянные и , для нахождения которых используются условия прохождения искомой экстремали через заданные точки и . Таким образом, решение задачи построения экстремали сводится к краевой задаче (или двухточечной), которая существенно отличается от задачи Коши, где решение удовлетворяет только начальным условиям. Двухточечная задача может и не иметь решения, когда задача Коши решение имеет.

Рассмотрим некоторые частные случаи уравнения Эйлера.

1. Функция не содержит , т.е. 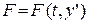. При этом 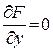, и уравнение Эйлера запишется в виде

.

Откуда следует , где - произвольная постоянная. Разрешая это уравнение относительно , получим:

.

Интегрируя его, найдем 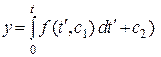, - произвольная постоянная. Таким образом, в этом случае уравнение Эйлера интегрируется полностью.

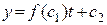2. В функцию не входят и . Тогда , и уравнение Эйлера преобразуется к виду , или . В этом случае . Экстремали представляют прямые линии.

Пример 1. Среди всех гладких кривых, соединяющих две заданные точк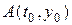и и найти такую, которая имеет минимальную длину. В этом случае

.

Подынтегральная функция не содержит и , а искомая экстремаль по только что доказанному представляет прямую , проходящую через заданные точки. Постоянные и находятся из системы уравнений

Пример 2. Рассмотрим обтекание тонкого профиля (рис. 7) в линеаризованном сверхзвуковом потоке [2]. Пусть передняя кромка находится в начале координат 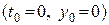, а задняя – в точке 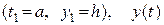- ордината точки профиля. Тогда волновое сопротивление профиля можно представить в виде [2]

, где - коэффициент пропорциональности, зависящий от плотности и скорости набегающего потока.

Так как не зависит от и , уравнение экстремали имеет вид . Удовлетворяя граничным условиям, найдем .

Это отрезок прямой линии. Но какой экстремум реализует эта прямая остается неизвестно. Необходимы дополнительные исследования.

Замечание. При выводе уравнения Эйлера предполагали, что - скалярная функция. В том случае, когда - есть векторная функция размерности , подынтегральная функция имеет вид , а граничные точки A и B задаются в - мерном пространстве . В этом случае

.

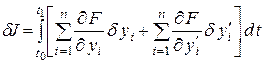Используя необходимое условие экстремума 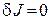, и основную лемму вариационного исчисления, получим систему уравнений второго порядка

(1.19)

Общее решение этой системы содержит констант, для определения которых имеет условий.

 

2.5. Уравнение Эйлера-Пуассона.

Рассмотрим задачу поиска экстремума функционала

,

.

В этой задаче закрепленными являются значения функции , но и ее производной в точках и . Допустимыми являются только дважды непрерывно дифференцируемые функции, удовлетворяющие этим концевым (граничным) условиям.

Первую вариацию

,

учитывая формулы

,

,

и при и ,

преобразуем к виду

.

Применяя основную лемму вариационного исчисления, получим Уравнение Эйлера – Пуассона:

.

Это уравнение четвертого порядка. Решения его зависит уже от 4-х констант, которые находятся из условия прохождения экстремали через заданные граничные точки.

 

2.6. Вариационные задачи с нефиксированными границами. Условие трансверсальности.

При рассмотрении простейшей задачи вариационного исчисления предполагалось, что граничные точки A и B являются заданными. В прикладных задачах эти точки могут быть не фиксированы, т.е. могут быть свободны все или частично. Можно выделить, например, следующие случаи:

1. Координаты точек A и B свободны( -не заданы).

2. Точка A – задана, точка B свободна ( - заданы, - не заданы).

3. Точка A задана, координаты т. B связаны зависимостью .

4. Координаты точек A и B связаны совокупностью условий

Могут рассматриваться и другие варианты.

Однако общим для всех вариантов является наличие некоторой свободы в выборе параметров граничных точек. В этих случаях свободные параметры можно рассматривать как дополнительные управляющие параметры и доопределять их в процессе решения вариационной задачи.

Как и ранее, найдем приращение функционала (1.13). При нефиксированных граничных условиях

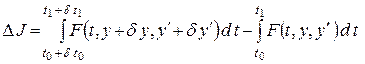
представим в следующем виде

где - независимые вариации параметров и .

Воспользовавшись формулой Тейлора и теоремой о среднем, получим

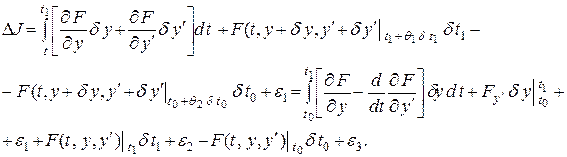(1.20)

где , - величины более высокого порядка малость чем .

Поскольку искомая экстремаль при нефиксированных граничных точках должна быть экстремалью и среди кривых сравнения, имеющих с нею общие граничные точки, она должна удовлетворять уравнению Эйлера и должно выполняться уравнение.

(1.21)

Тогда из (1.20) следует, что

(1.22)

В выражение (1.22), кроме независимых вариаций входят, так называемые изохронные вариации , которые не являются независимыми. Выразим изохронные вариации через приращения конечных значений и . Поскольку эта зависимость нелинейная, то линеаризируя ее, получим (рис. 8).

,

,

или

,

.

Используя полученные соотношения, найдем из (1.22) и (1.11)

(1.23)

Полученное условие может быть использовано для определения оптимальных значений координат граничных точек. Оно называется условием трансверсальности и используется совместно с уравнением Эйлера.

Рассмотрим некоторые частные условия трансверсальности.

1. Точки A и B заданы. В этом случае , условие (1.23) выполняется тождественно и дополнительной информации не дает.

2. Координаты и 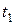, заданы, а и 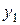произвольны. В этом случае и из условия трансверсальности получаем дополнительно два условия для определения и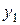

3. Точка A задана, а координаты точки B связаны зависимостью . В этом случае 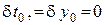, а вариации и связаны зависимостью

,

и из условия трансверсальности получим недостающее условие

.

В том случае, когда y(t) – n – мерный вектор достаточно гладких функций, искомая экстремаль удовлетворяет системе уравнений Эйлера

(1.24)

а условие трансверсальности имеет вид:

(1.25)

Из условия трансверсальности можно получить систему соотношений для определения граничных значений параметров . В общем случае эти параметры могут быть связаны условиями

, (1.26)

тогда соответствующая система уравнений в вариациях будет иметь вид:

(1.27)

Используя полученную систему линейных алгебраических уравнений (1.27), можно выразить зависимых переменных через 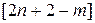независимых переменных и из условия трансверсальности (1.25) получить 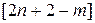уравнений, которые совместно с (1.26) дают замкнутую систему уравнений для определения переменных (координат граничных точек).

 

2.7. Вариационные задачи на условный экстремум.

До сих пор мы рассматривали задачи поиска функций из заданного класса, доставляющих экстремум функционалу 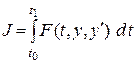. При этом рассматривались случаи фиксированных или нефиксированных граничных условий. Других ограничений на выбор функций сравнения не было. Однако, при решении прикладных задач при принятии того или иного решения, в том числе оптимального, всегда приходится учитывать совокупность ограничений по энергопотреблению, быстродействию, точности, (текущей или конечной), надежности и т.п. Эти ограничения всегда будут накладывать ограничения на выбор допустимых вариаций. Поиск экстремума функционала при наличии дополнительных ограничений (связей), называется задачей на условный экстремум.

Обычно различают связи трех типов:

а) голономные связи – связи, не содержащие производных искомых функций

;

б) неголономные связи – связи, содержащие производные искомых функций

;

в) изопериметрические (интегральные связи)

.

Вариационные задачи на условный экстремум при голономных и неголономных связях можно (теоретически) решить методом исключения зависимых переменных. Тогда задача на условный экстремум сводится к задаче на безусловный. Однако такой подход практически неприменим ввиду сложности процедур исключения зависимых переменных. Поэтому наибольшее распространение получил метод множителей Лагранжа. Рассмотрим применение этого мето